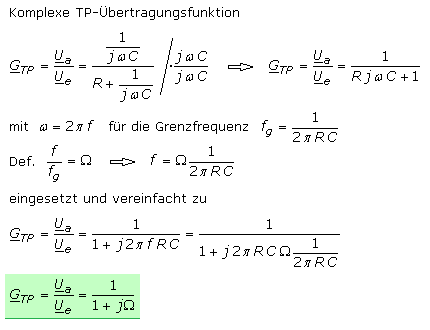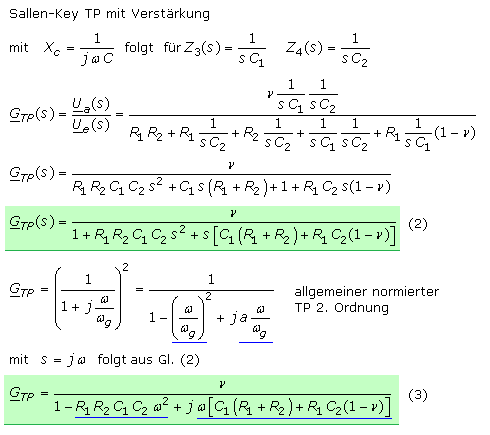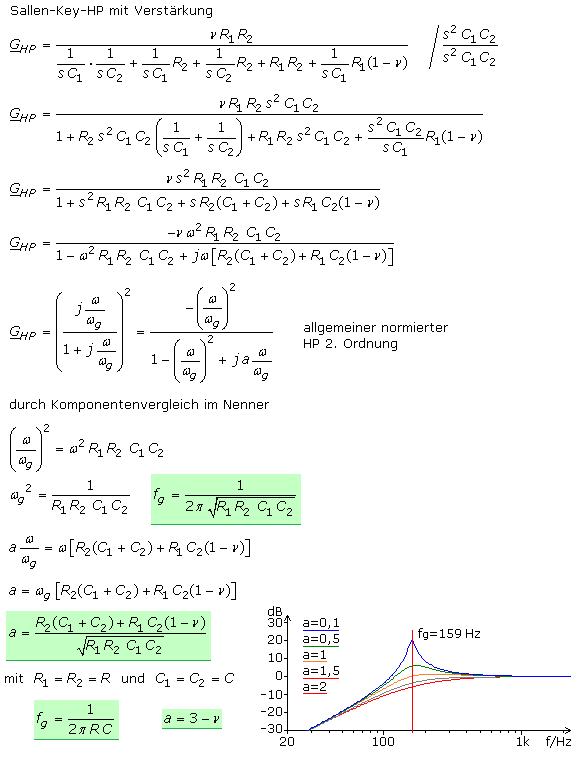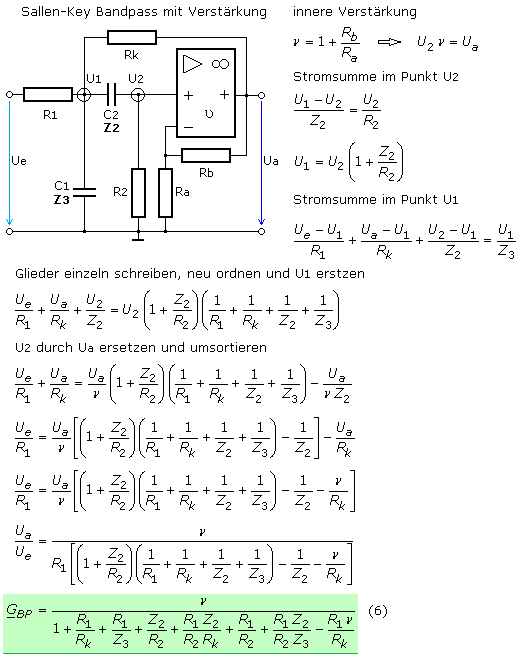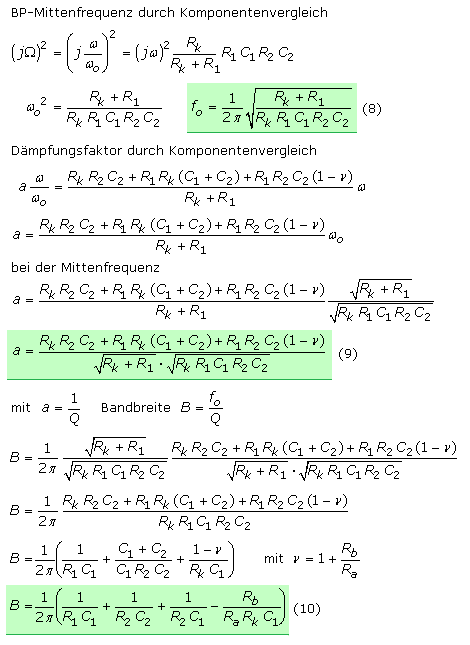Aktive RC-Filterschaltungen

Mit Filterschaltungen wird zum Beispiel die Signalamplitude, der zeitliche Signalverlauf und Signallaufzeiten elektrischer Signale beeinflusst. Lineare RC- und RL-Filter verändern bei sinusförmigen Signalen sowohl das Amplitudenverhältnis zwischen Eingangs- und Ausgangssignal als auch ihre Phasenlage. Bei modulierten Signalen sind die Signallaufzeiten bestimmter Frequenzbänder wichtig. In passiven Filtern belasten sich die zusammengeschalteten TP- und HP-Glieder gegenseitig und mit jeder weiteren Stufe verringert sich die Ausgangsamplitude. In aktiven Filtern sind die Einzelglieder gegenseitig entkoppelt, sodass man die Verstärkung, Flankensteilheit und weitere Filtercharakteristiken gezielt beeinflussen kann.

Aktive Filter eignen sich für den Bereich der Informationsübertragung und weniger bis gar nicht zur Energieübertragung. In der analogen Signaltechnik sind es meistens RC-Filter mit OPV-Schaltungen. Induktivitäten, die im niedrigen Frequenzbereich besonders große Werte haben müssten, sind voluminös und in integrierter Technik nicht herzustellen. Sie werden durch Impedanzkonverter oder Gyratorschaltungen optimal ersetzt.

Filter werden oft anhand ihres Frequenzverhaltens charakterisiert und mithilfe der frequenzabhängigen Übertragungsfunktion mathematisch beschrieben. Vorteilhaft sind die Anwendung der komplexen Wechselstromrechnung und eine Vereinfachung durch die Normierung auf den Wert der Grenzfrequenz beim Hoch- oder Tiefpass mit Ω = f / fg oder den Bezug auf die Mittenfrequenz beim Bandpass oder der Bandsperre. Sie errechnet sich durch Ziehen der Wurzel aus dem Produkt der beiden Eckfrequenzen zu: fm = √(fg1·fg2). Für die Frequenzabhängigkeit j·ω = j·2·π·f wird in einigen Veröffentlichungen die komplexe Frequenzvariable (p) oder in der englischen Literatur (s) verwendet. Für einen Tiefpass wird die Übertragungsfunktion etwas ausführlicher hergeleitet.

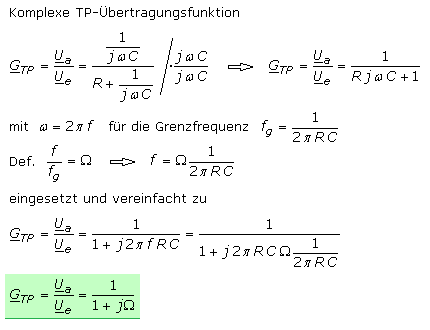
Ein Tiefpass in Serie mit einem Hochpass ergibt einen Bandpass, während die Parallelschaltung der Pässe mit unterschiedlichen Grenzfrequenzen zur Bandsperre wird. Die Impedanzwandler sorgen für eine belastungsfreie Entkopplung zwischen den Pässen. Im dargestellten Beispiel sind die Grenzfrequenzen vom Tief- und Hochpass mit fg = 159 Hz gleich und somit hat auch der Bandpass diese Mittenfrequenz. Die Ausgangsamplitude bei dieser Frequenz errechnet sich zu −6 dB und wird von der Simulation bestätigt. Bei der Bandsperre wurden für den Tiefpass 159 Hz und für den Hochpass 1,59 kHz als Grenzfrequenz gewählt. Die Simulation bestätigt die errechnete Mittenfrequenz von 503 Hz.

Der einfache Integrator und Differenziator in einer rückgekoppelten invertierenden OPV-Schaltung ist in diesem Webprojekt ausführlich beschrieben worden. In diesen Schaltungen bestimmt das Widerstandsverhältnis die Grundverstärkung und hat auch Einfluss auf die Grenzfrequenz. Bei den nicht invertierenden OPV-Schaltungen sind beide Eigenschaften voneinander unabhängig.

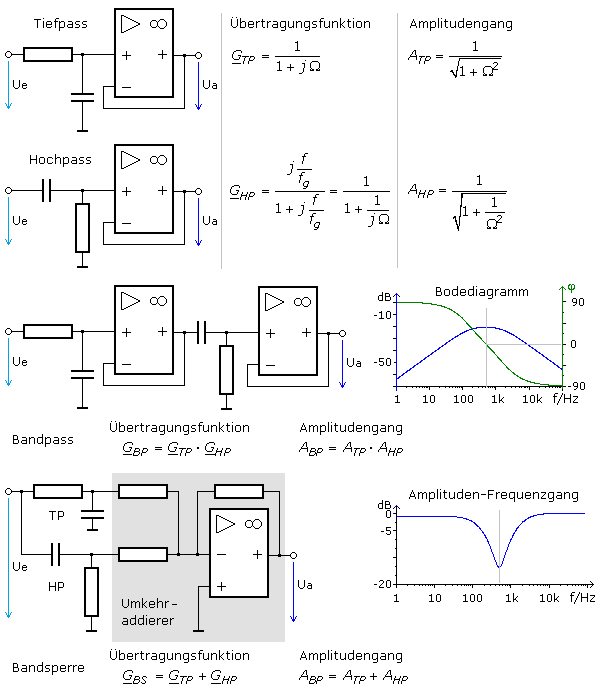
Für den Bereich sehr niedriger Frequenzen für Ω « 1 errechnen sich für den Tiefpass Amplitudenwerte nahe eins. Für Ω = 1 bei Grenzfrequenz hat die Ausgangsamplitude den Wert 1 / √2 = 0,707. Für den Bereich sehr hoher Frequenzen mit Ω » 1 ist die Ausgangsamplitude nahe 1 / Ω. Für jede weitere Frequenzdekade nimmt die Ausgangsamplitude um 20 dB ab.

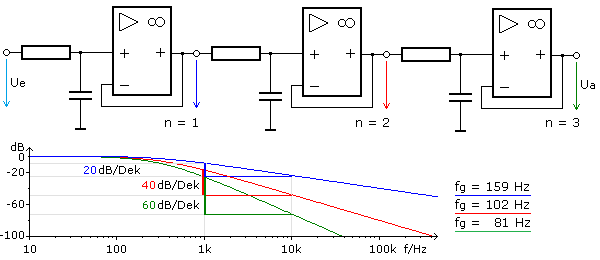
Die Schaltung zeigt einen TP 3. Ordnung mit drei gleichen, durch Impedanzwandler entkoppelten Stufen. Bei der Serienschaltung mehrerer TP- oder Hochpassglieder errechnet sich der Amplitudengang durch die Multiplikation der Einzelglieder. Die Herleitung zeigt, dass die Flankensteilheit mit jeder Stufe um 20 dB pro Dekade zunimmt.

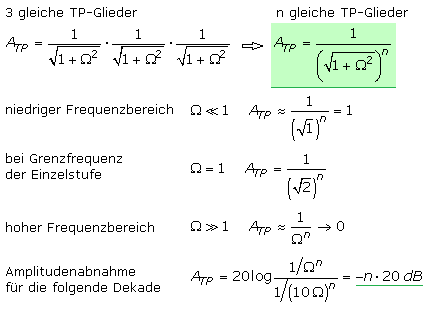
Die Simulation zeigt, dass bei gleichen TP-Gliedern mit zunehmender Ordnungszahl die Grenzfrequenz für das gesamte Filter abnimmt. Bei einem mehrstufigen HP-Filter ist die Grenzfrequenz größer als die des Einzelglieds. Auf die Grenzfrequenz der Einzelstufe mit Ω = 1 bezogen verringert sich bei beiden Filtertypen die Ausgangsamplitude eines n-stufigen Filters um n·3 dB. Die Grenzfrequenz des Filters errechnet sich aus der Grenzfrequenz der gleichen Einzelstufen durch Multiplikation mit dem Faktor α. Für den Fall der kritischen Dämpfung kann α wie folgt hergeleitet werden kann.

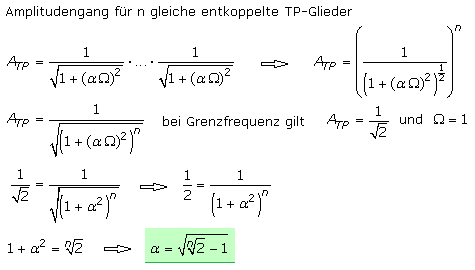
Das klassische passive Filter 2. Ordnung ist eine RCL-Schaltung und hat zwei unabhängige Speicherelemente. Die Dämpfung beträgt 40 dB pro Dekade. Der Amplituden-Frequenzgang zeigt beim Übergang vom Durchlass- in den Sperrbereich eine von der Dimensionierung abhängige Überhöhung. Dieser Effekt tritt bei den bisher vorgestellten aktiven Filtern höherer Ordnung nicht auf. Er kann durch eine von der Frequenz abhängige Mitkopplung auch bei aktiven RC-Filtern erreicht werden.

Sallen-Key-Filter

Diese aktiven Filter 2. Ordnung sind nach ihren Entwicklern R. P. Sallen und E. L. Key benannt. In den meisten Fällen wird der OPV mit einer Einfachmitkopplung betrieben. Mit einem ohmschen Spannungsteiler am invertierenden Eingang kann der Verstärkungsfaktor V>1 festgelegt werden. Das Filter kommt ohne Induktivitäten aus und hat eine Resonanzstelle (Polstelle) wie ein RCL-Filter. Die Sallen-Key-Schaltung ist für Tiefpass-, Hochpass- und Bandpassfilter geeignet. Man kann sie in Serie schalten und durch Filterstufen 1. Ordnung zu Filtern mit ungerader Ordnung erweitern.

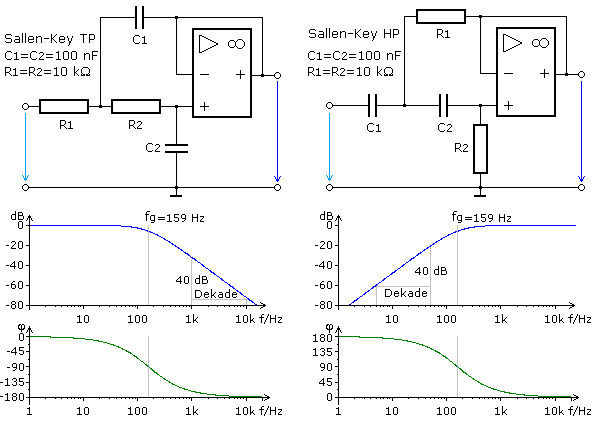
Das Bild zeigt die Grundschaltung für einen Tiefpass und Hochpass gleicher Dimensionierung mit Einfachmitkopplung. Die prinzipielle Funktion der Schaltungen kann mit Eingangssignalen sehr niedriger und sehr hoher Frequenz ermittelt werden. Liegen sehr tiefe Frequenzen am TP-Eingang an, dann sind sowohl C1 als auch C2 sehr hochohmig. Das Eingangssignal gelangt direkt an den P-Eingang des OPVs und über die Rückkopplung unverändert an den N-Eingang. Das Ausgangssignal entspricht dem Eingangssignal. Bei sehr hohen Frequenzen sind beide Kondensatoren in der TP-Schaltung extrem niederohmig. Der P-Eingang des OPVs liegt quasi auf Masse. Da im Arbeitsbereich des OPVs die Spannungsdifferenz zwischen beiden Eingängen praktisch 0 V beträgt, hat auch das Ausgangsignal quasi 0 V. Es handelt sich um einen Tiefpass.

Liegen bei der rechten HP-Schaltung tiefe Frequenzen am Eingang an, dann sind die Kondensatoren C1 und C2 so hochohmig, dass kein Signal an den P-Eingang des OPVs gelang, der über den Widerstand R2 an Masse liegt. Das Ausgangssignal ist dann ebenfalls quasi 0 V. Bei sehr hohen Frequenzen sind beide Kondensatoren nahe einem Kurzschluss. Die gesamte Amplitude des Eingangssignals liegt am P-Eingang des OPVs und die Amplitude des Ausgangssignals ist wegen der Verstärkung 1 des Impedanzwandlers gleich groß. Im Sperrbereich haben beide Pässe eine Dämpfung von 40 dB pro Dekade. Bei der Grenzfrequenz ist die Ausgangsamplitude 6 dB niedriger als die Eingangsamplitude. Bei gleicher Bauteildimensionierung errechnet sich die Grenzfrequenz zu: fg = 1 / 2·π·(R·C), wobei es noch zu keiner Überhöhung kommt.

Zur Herleitung einer allgemeinen Übertragungsfunktion ersetzt man die Bauteile durch Impedanzen. Da der OPV als ideal angenommen wird, hat die Schaltung bei A nur einen Stromknoten. Mit der komplexen Frequenzvariablen p = s = j·ω bleiben die Formeln übersichtlicher.

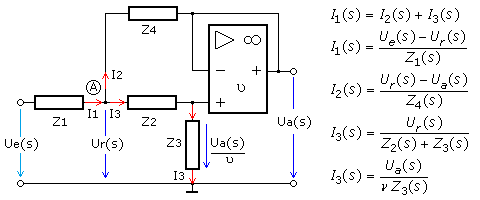
Sallen-Key-Tiefpass 2. Ordnung

Für die oben dargestellte Sallen-Key-Schaltung sind beim Tiefpass 2. Ordnung die Impedanzen Z1 und Z2 ohmsche Widerstände während Z3 und Z4 kapazitive Blindwiderstände darstellen. In die Gl.(1) eingesetzt folgt die Übertragungsfunktion des TP-Filters.

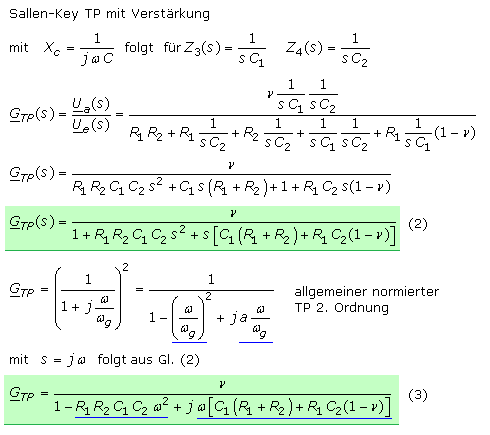
Durch einen Vergleich sich entsprechender Komponenten im normierten allgemeinen TP-Filter 2. Ordnung können Grenzfrequenzen und Dämpfungswerte (a) für unterschiedliche Dimensionierungen von R und C ermittelt werden. Für den speziellen Fall gleicher Bauteildimensionierungen vereinfachen sich die Gleichungen Gl.(4) und Gl.(5). Die Simulationsergebnisse für unterschiedliche Verstärkungen sind auf den Ausgangswert 0 dB gesetzt. Die Amplitudenüberhöhung nimmt bei Verstärkungen größer 1,5 deutlich zu. Die Dämpfung mit dem Verstärkungsfaktor 3 aufzuheben ergibt keinen Sinn, da in der Gl.(5) der Nenner nicht null werden darf und die Schaltung bei der Grenzfrequenz zum Schwingen neigt.

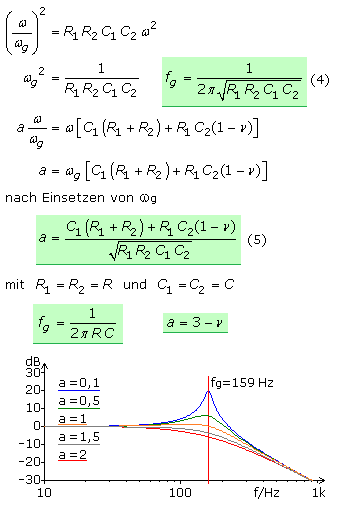
Ein Filter mit dem Dämpfungsfaktor a = 2 hat einen Impedanzwandler mit der Verstärkung 1 und ist ein Filter mit kritischer Dämpfung. Eine Sprungfunktion am Eingang führt zu keinem Überschwingen. Nachteilig ist der langsame Übergang vom Durchlass- in den Sperrbereich. Da in aktiven Filtern die Einzelstufen durch die Verstärker gegenseitig entkoppelt sind, können sie durch eine einfache Serienschaltung zu Filtern höherer Ordnung erweitert werden.

Sallen-Key-Hochpass 2. Ordnung

Beim Hochpass sind Z1 und Z2 die kapazitiven Blindwiderstände, während Z3 und Z4 ohmsche Widerstände sind. In die Gl.(1) eingesetzt erhält man die Übertragungsfunktion des HP-Filters. Werden die Gleichungen mit denen für den TP verglichen, erkennt man, dass die Stellen der ohmschen und kapazitiven Widerstände getauscht sind. Für verschiedene Verstärkungen sind die Simulationsergebnisse im Durchlassbereich auf die gleiche Ausgangsamplitude 0 dB bezogen dargestellt. Bei gleicher Dimensionierung der Bauteile ist das Filterverhalten bei getauschtem Durchlass- und Sperrbereich identisch.

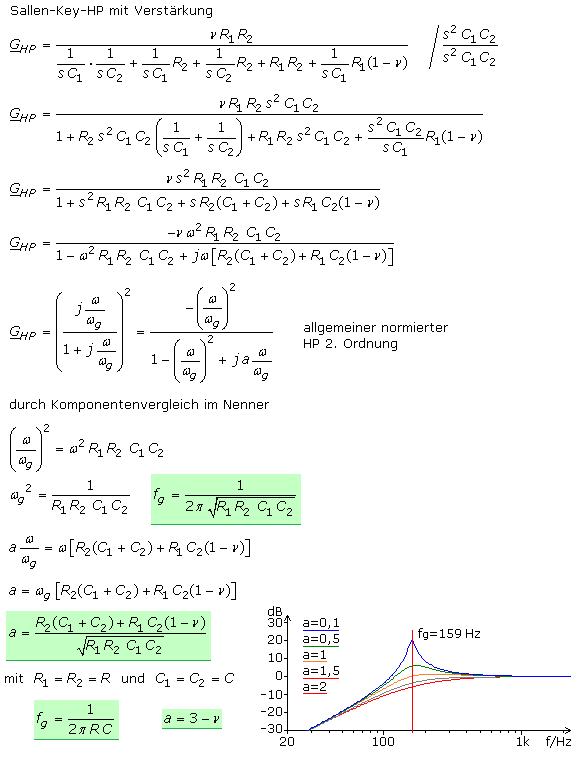
Für den Sallen-Key Hoch- und Tiefpass mit nicht invertierendem OPV und zusätzlicher Verstärkung kann die normierte Übertragungsfunktion auch wie folgt angegeben werden. Mit dem Wert α = 1 entfällt die Gegenkopplung und der OPV arbeitet mit der Verstärkung 1 als reiner Impedanzwandler. Mit R1 = R2 und C1 = C2 ergeben sich weitere Vereinfachungen. Die Filtereigenschaften sind dann abhängig vom Verstärkungsfaktor α.

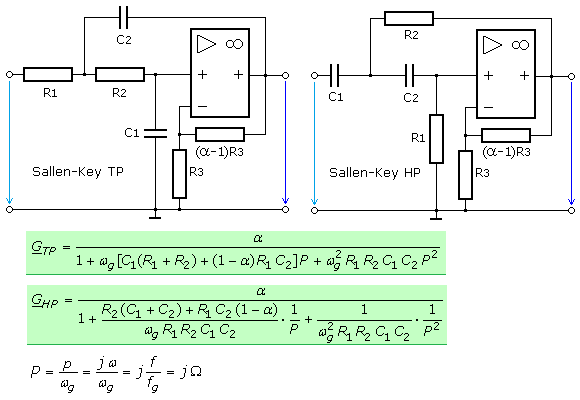
Das folgende Übertragungsdiagramm zeigt, dass bei unveränderten Werten für R und C die Filtereigenschaften vom Verstärkungsfaktor α bestimmt werden. Nach dem höchsten Exponenten der Übertragungsfunktion handelt es sich um einen Sallen-Key-TP 2. Ordnung, was durch den Dämpfungsverlauf im Sperrbereich bestätigt ist.

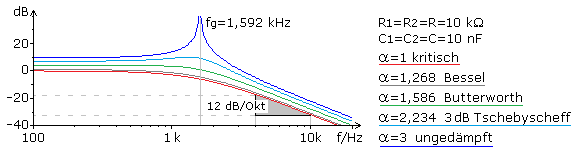
Bandpass mit Sallen-Key Filterglieder

Die Serienschaltung eines Sallen-Key-HP mit einem Sallen-Key-TP mit ausreichend unterschiedlichen Grenzfrequenzen ergibt einen Bandpass. Die OPVs verhindern die gegenseitige Belastung der beiden Pässe. Die Filtergüte ist das Verhältnis der Mittenfrequenz zur Bandbreite. Die Verstärkung beeinflusst die Filtercharakteristik vergleichbar mit dem Koppelfaktor bei passiven LC-Bandfiltern. Die Simulationsreihe zeigt die Übertragungsfunktionen für verschiedene Verstärkungsfaktoren. Die Grenzfrequenz für den Hochpass beträgt fu = 796 Hz und für den Tiefpass fo = 1592 Hz. Damit errechnet sich die Mittenfrequenz des Bandpassfilters zu fr = 1125 Hz. Die Bandbreite ist mit B = 1100 Hz von der Verstärkung unabhängig, sodass auch die Güte mit Q ≈ 1 gleich bleibt.

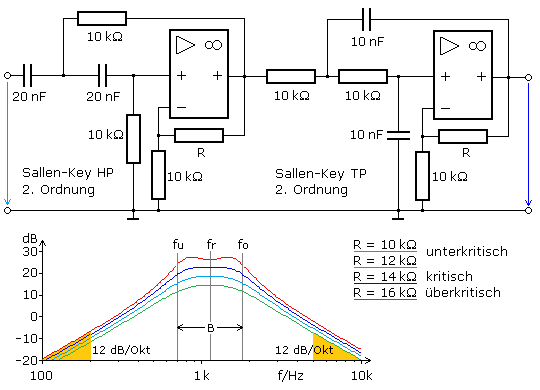
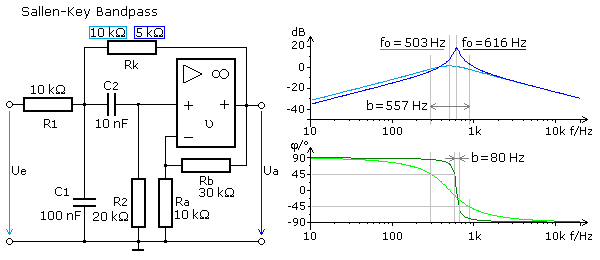
Sallen-Key Bandpass mit Einfachmitkopplung

Das folgende Bild zeigt der Sallen-Key Schaltung entsprechend eine kompaktere Schaltung mit nur einem OPV und einem zusätzlichen ohmschen Widerstand. Beim nicht invertierenden OPV kann mit dem Spannungsteiler am N-Eingang eine interne Verstärkung größer 1 eingestellt werden. Für diese Schaltung folgt die allgemeine Herleitung der Übertragungsfunktion in Einzelschritten. Der OPV entkoppelt nur einen HP und TP 1.  Ordnung, wodurch die Dämpfung im Sperrbereich nur 20 dB pro Dekade erreicht.

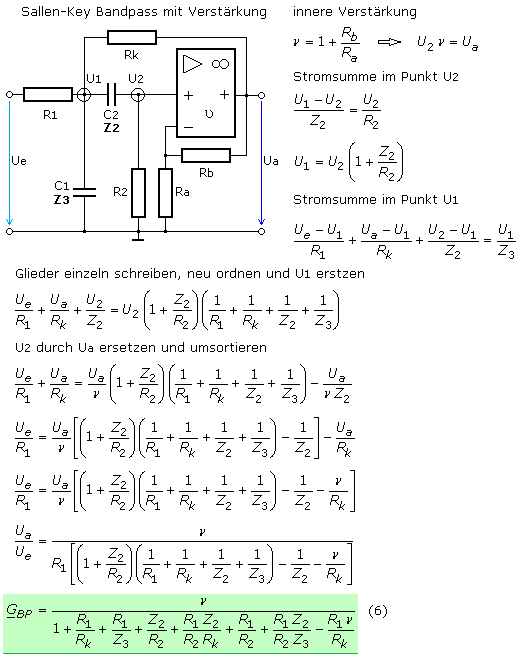
Zur Herleitung der frequenzabhängigen Übertragungsfunktion werden die beiden Impedanzen durch ihre komplexen Größen ersetzt. Wie in den vorangegangenen Beispielen wird für die Übertragungsfunktion eine Darstellung angestrebt, die einen Komponentenvergleich mit der allgemeinen normierten Übertragungsfunktion für einen Bandpass ermöglicht. Für den Bandpass erhält man diese Funktion durch Multiplikation der normierten Übertragungsfunktionen für den Tiefpass und Hochpass 1. Ordnung.

Ein Bandpass hat drei charakteristische Frequenzen. Die untere Grenzfrequenz wird vom Hochpass und die obere Grenzfrequenz vom Tiefpass bestimmt. Die maximale Ausgangsspannung wird bei der Mittenfrequenz f0 erreicht, die mit der Gleichung Gl.(8) errechnet werden kann. Die Bandbreite B (b) errechnet sich aus der Differenz zwischen oberer und unterer Grenzfrequenz. Durch Komponentenvergleich erhält man bei der Mittenfrequenz den Dämpfungsfaktor a nach Gl.(9). Sein Kehrwert ist die Güte Q und umgekehrt proportional zur Bandbreite B, die nach Gl.(10) berechnet werden kann.

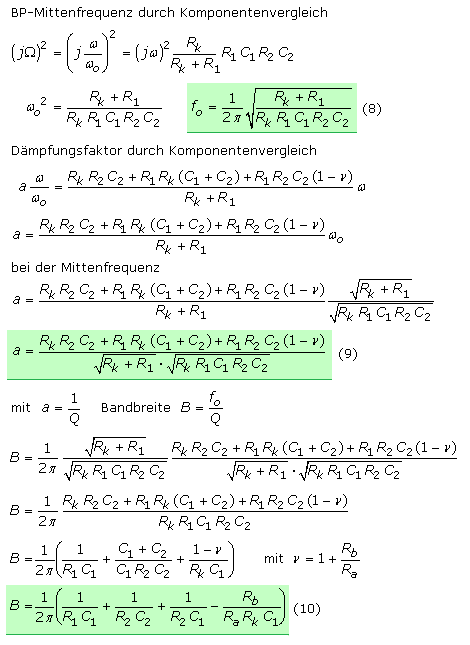
Die Messwerte einer Schaltungssimulation stimmen mit den errechneten Werten überein. Die Schaltung entspricht einem Filter 1. Ordnung, da die Flankensteilheit im Sperrbereich maximal 20 dB pro Dekade erreicht. Wird bei gleichbleibender Verstärkung der Wert des Rückkoppelwiderstands weiter verringert, geht die Bandbreite gegen null. Mit Werten unter 5 kΩ arbeitet die Schaltung bei einer höheren Mittenfrequenz und deutlich größerer Bandbreite weiter. Die Schaltung funktioniert auch mit der V = 1 und dem OPV als Impedanzwandler. Die Ausgangsamplitude ist unabhängig vom Wert des Rk und erreicht rund −16 dB.

Filter mit Mehrfachgegenkopplung

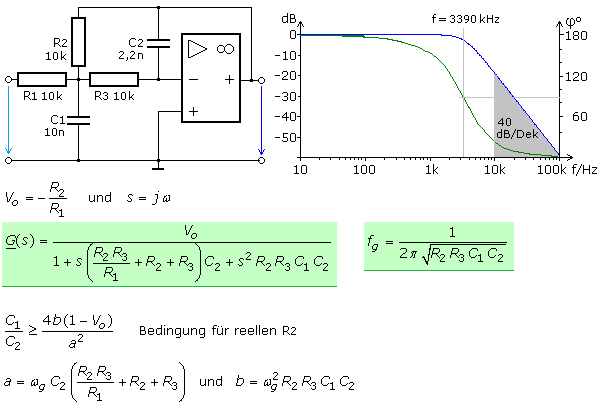
Aktive Hoch- und Tiefpässe sind auch mit mehrfach gegengekoppelten invertierenden OPV-Schaltungen möglich. Die folgende Schaltung zeigt einen Tiefpass 2. Ordnung und die Übertragungsfunktion. Auf die umfangreichen mathematischen Betrachtungen habe ich bewusst verzichtet. Zur korrekten Dimensionierung ist die angegebene Bedingung zu beachten. In den meisten Fällen werden die Werte der Kondensatoren vorgeben, da ihr Toleranzbereich eingeschränkter als die der Widerstände ist.

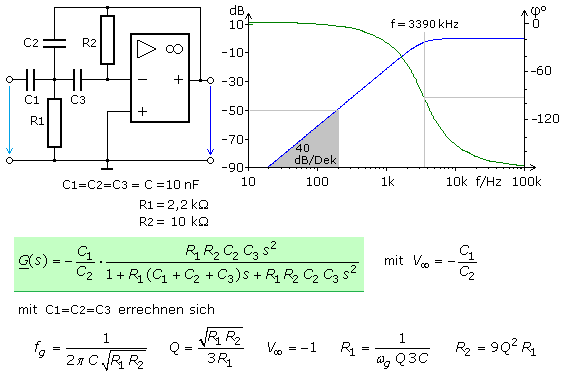
Werden anstelle der Widerstände Kondensatoren und für die Kondensatoren Widerstände eingesetzt, erhält man einen Hochpass 2. Ordnung. Die allgemeine mathematische Herleitung ist fast immer sehr umfangreich. Normalerweise werden zur Dimensionierung die Kondensatoren vorgegeben und die Widerstandswerte errechnet. Vielfach werden bestimmte Vereinfachungen durch gleiche Widerstands- und Kondensatorwerte vorgenommen. Für Filtergrundglieder und bestimmte Filtercharakteristiken bestehen Parameterlisten, die in der Literatur und im Internet zu finden sind.

Bandpass mit Mehrfachgegenkopplung

Die prinzipielle Arbeitsweise kann durch Grenzbetrachtungen ermittelt werden. Für niederfrequente Eingangssignale sind die Blindwiderstände beider Kondensatoren sehr hoch und die Verstärkung des OPVs nimmt proportional mit der Eingangsfrequenz zu. Für hochfrequente Eingangssignale ist der Kondensator C1 sehr niederohmig. Dieser Frequenzbereich gelangt vom OPV verstärkt und invertiert über den ebenfalls niederohmigen C2 auf den Eingangsknoten zurück. Die Addition der Signale bildet das in der Amplitude geschwächte wirksame Eingangssignal für den OPV. In der Praxis wird der Bandpass mit gleichen Kondensatoren aufgebaut.

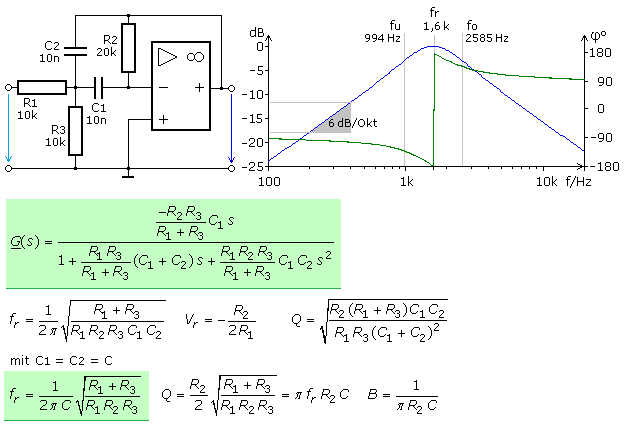
Die Verstärkung Vr bei der Mittenfrequenz ist ebenso wie die Bandbreite B vom Widerstand R3 unabhängig. Ohne diese Parameter zu beeinflussen, kann folglich mit R3 die Mittenfrequenz bestimmt werden. Die Schaltung arbeitet auch ohne R3 als Bandpass, allerdings mit weniger Freiheitsgraden.