Synthese digitaler Schaltungen

In diesem Kapitel wird für eine einfache Automatenschaltung eine digitale Steuerschaltung entwickelt. Anschließend wird mithilfe der disjunktiven Normalform und Mintermen oder der konjunktiven Normalform und Maxtermen eine Schaltungsoptimierung auf einen Gattertyp gezeigt.

Viele Funktionen des täglichen Lebens beruhen auf dem Zusammenwirken einfacher Schaltimpulse. Mit den binären Signalen EIN und AUS lassen sich geeignete digitale Schaltungen entwickeln, die mit möglichst wenig Schaltungsaufwand durch logische Verknüpfungen die gewünschte Funktion ausführen. Letztendlich strebt man eine Lösung mit wenigen Gattern des gleichen Typs an.

Eine Schaltungssynthese beginnt mit einer eindeutigen Beschreibung der Funktionalität. Dazu eignet sich das Aufstellen einer Wahrheitstabelle. Normalerweise werden zur Bezeichnung der Variablen Großbuchstaben benutzt. Die Eingangsvariablen erhalten Anfangsbuchstaben des Alphabets und die Ausgangsvariablen Endbuchstaben. Ist die Abhängigkeit der logischen Zustände untereinander festgelegt, kann die Wahrheitstabelle geschrieben und nach einer Schaltungsoptimierung gesucht werden. Die Schritte einer Schaltungssynthese in Zusammenfassung:

• Funktionsbeschreibung der gewünschten Schaltung.
• Bezeichnen der Eingangs- und Ausgangsvariablen.
• Definieren der voneinander abhängigen Zustände 0 und 1.
• Aufstellen der Wahrheitstabelle.
• Erstellen der logischen Verknüpfungsschaltung.
• Schaltungsoptimierung zum Einsatz von nur NAND- oder NOR-Gatter.

Schaltungssynthese einer digitalen Verriegelungsschaltung

Eine Sicherheitsschaltung soll das Abfahren einer Förderanlage bei festgelegten Bedingungen verhindern. Es sind drei Eingangsvariablen und eine Ausgangsvariable vorgesehen.

• A: Die Anlage darf bei offenem Türkontakt nicht fahren. Offen: A = 0, geschlossen A = 1.
• B: Die Anlage darf bei geschlossenem Überlastkontakt nicht fahren. Geschlossen B = 1, offen B = 0.
• C: Anlage steht bei nicht betätigtem Etagenknopf. Offen C = 0, geschlossen C = 1.
• Z: Die Anlage fährt bei der Ausgangsvariablen Z = 1. Bedingung: A = 1 und B = 0 und C = 1.

Die Aufgabe verwendet drei Eingangsvariablen mit jeweils zwei Möglichkeiten bei insgesamt 2³ = 8 Zuständen. Die Wahrheitstabelle kann aufgestellt werden. Damit die Ausgangsvariable Z = 1 wird, müssen die angegebenen drei Bedingungen erfüllt sein. In allen anderen Fällen ist Z = 0.

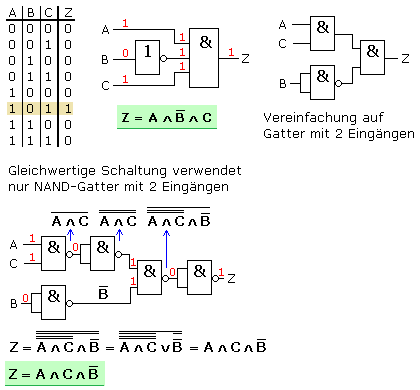
Die Wahrheitstabelle zeigt, dass die Anlage nur bei der einer erlaubten Kombination freigeschaltet ist. Der Schaltungsaufbau kann auf Gatter mit nur zwei Eingängen vereinfacht und auf die Verwendung von NAND-Gattern optimiert werden. Der mathematische Lösungsweg nach De Morgan zeigt die Richtigkeit. Mehrfache Negierungen werden von innen nach außen aufgelöst, wobei doppelte Negierungen das Argument nicht verändern und wegfallen können.

Entwicklung einer digitalen Automatensteuerung

Ein Getränkeautomat gibt nach Einwurf einer Münze entweder Tee oder Kaffee aus, wenn die entsprechende Wahltaste betätigt wurde. Beide Wahltasten gleichzeitig gedrückt verhindern die Ausgabe. In der Maschine gibt es je ein Magnetventil für Wasser, Kaffee- und Tee-Extrakt. Der Ausschank erfolgt bei geöffnetem Wasserventil und einem dazu offenen Ventil für entweder Tee oder Kaffee.

Die Maschine kennt drei Eingangsvariable für insgesamt 8 Kombinationen, den Münzschalter (A), den Tee- (B) und den Kaffeewahlschalter (C). Drei Ausgangsvariablen stehen für das Wasser-, Tee- und Kaffeeventil. Die drei Funktionsgleichungen sind von den Eingangszuständen abhängig und dürfen nur zwei eindeutige Ergebnisse liefern.

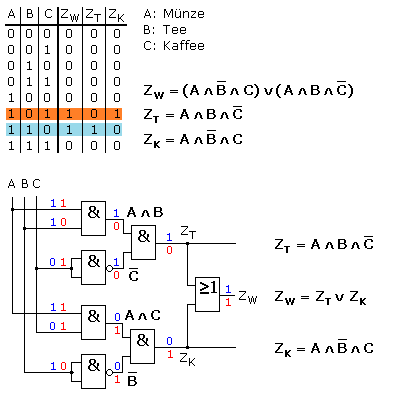
In beiden Beispielen wird die Funktionsgleichung aus einer UND-Verknüpfung der Eingangsvariablen gebildet, deren Ergebnis eine logische 1 hat. Treten wie im zweiten Beispiel in der Wahrheitstabelle mehrere dieser Zustände auf, sind diese zum Erhalt der Funktionsgleichung noch durch ODER zu verknüpfen.

Disjunktive Normalform – DNF

Die disjunktive Normalform (DNF), auch ODER-Normalform, ist ein logischer Ausdruck, wo die Glieder in der obersten Rechenebene durch ODER-Verknüpfungen verbunden sind. Ist die Wahrheitstabelle bekannt, so werden für jede Zeile mit dem Ausgangswert 1 die Vollkonjunktionen (UND-Verknüpfungen) erstellt. In jeder Vollkonjunktion sind alle Eingangsvariablen genau einmal vorhanden und müssen zum Teil negiert werden, damit für die Ausgangsvariable der Wert 1 erfüllt ist.

Die ODER-Normalform ist auf besondere Weise mit einer Wahrheitstabelle verbunden, denn die Zahl der logischen 1-Zustände der Ausgangsvariablen ist gleich der Anzahl der Vollkonjunktionen der DNF. Die logischen 1-Zustände des Ausgangs werden als Minterme bezeichnet.

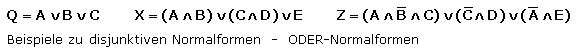
Minterme

Im Minterm sind alle Eingangsvariablen nur einmal enthalten, wobei sie normal oder negiert auftreten können. Bei n Variablen kann es 2ⁿ Minterme geben. Da es sich um eine UND-Verknüpfung der Eingangsvariablen handelt, hat jeder Minterm für nur eine bestimmte Eingangskombination den logischen Wert 1. Der Minterm entsteht aus dieser einen Eingangskombination, wenn alle Variablen im logischen Zustand 0 negiert mit denen im logischen Zustand 1 durch UND verknüpft werden. Das Bild zeigt passende Beispiele zu Mintermen.

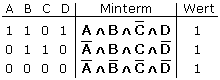
Die Funktionsgleichung (Z), die das gegebene Schaltnetz und damit die Wahrheitstabelle erfüllt, entsteht mithilfe der ODER-Normalform, der vollständigen disjunktiven Normalform (DNF). Man erhält Z durch ODER-Verknüpfungen derjenigen Minterme, mit den angepassten Eingangsvariablen, die den logischen Ausgangszustand 1 ergeben.

Die vollständige disjunktive Normalform (DNF) besteht aus nur einer Vollkonjunktion (UND-Verknüpfungen) oder mehreren Vollkonjunktionen mit dem logischen Zustand 1, die durch ODER verknüpft sind.

Im oben dargestellten Beispiel der Automatensteuerung erfolgt die Steuerung des Wasserventils durch die ODER-Normalform ZW. In ihr sind die Minterme zweier Vollkonjunktionen durch ODER verknüpft. Zur Steuerung des Tee- oder Kaffeeventils gehört ebenfalls je eine DNF, die aus nur einer Vollkonjunktion, dem Minterm ZT oder ZK besteht.

Beispiel zur DNF

Für eine aufgestellte Wahrheitstafel soll die Funktionsgleichung ermittelt werden. Das Schaltnetz ist danach für NAND-Gatter zu optimieren. Zuerst wird mithilfe der Wahrheitstafel die DNF notiert. Dazu werden die Minterme mit dem logischen Zustand 1 herausgeschrieben und durch ODER verknüpft. Die DNF kann oftmals noch vereinfacht werden.

Die Umformung zum Einsatz der NAND-Gatter erfolgt durch doppelte Negierung. Diese werden an den ODER-Verknüpfungen von innen nach außen aufgelöst, wobei aus dem ODER ein UND wird. Die doppelte Negierung einer Variablen liefert den Wert der Variablen und kann entfallen.

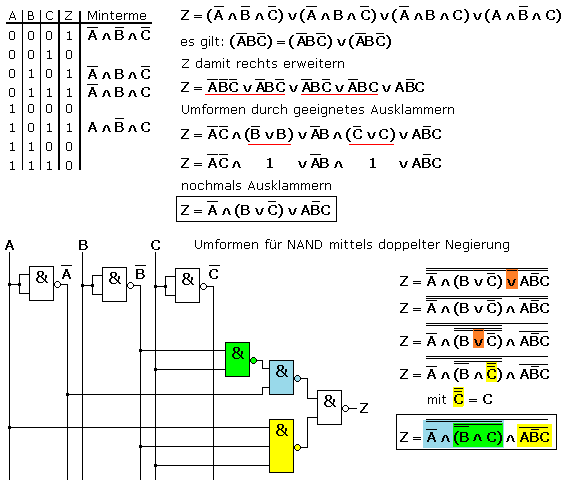
Stehen keine Simulationsprogramme zur Verfügung, sollte am Ende der Umformungen die Funktionsgleichung für alle Eingangskombinationen der Wahrheitstabelle überprüft werden und nicht nur für die Ausgänge mit logischer 1.

Konjunktive Normalform – KNF

Die konjunktive Normalform (KNF), auch UND-Normalform kann als Ergänzung oder Gegenpart zur disjunktiven Normalform gesehen werden. Die UND-Normalform ist ein logischer Ausdruck, dessen Glieder in der obersten Rechenebene durch UND-Verknüpfungen verbunden sind. Die Ausgangsvariable hat den Wert 0. Die Eingangsvariablen sind mit ODER verknüpft. Der Ausdruck wird als Volldisjunktion (ODER) bezeichnet, wenn alle Eingangsvariablen genau einmal vorkommen. Damit die Ausgangsvariable den Wert 0 annimmt, müssen Eingangsvariablen beim Erstellen der Volldisjunktion möglicherweise negiert werden.

Maxterme

Maxterme sind ODER-Verknüpfungen und verhalten sich wie Minterme mit dem Unterschied, dass jetzt der logische 0-Zustand betrachtet wird. Im Maxterm sind alle Eingangsvariablen nur einmal enthalten, wobei sie normal oder negiert sein können. Bei n Eingangsvariablen können 2ⁿ Volldisjunktionen auftreten. Beim Aufstellen der Maxterme für jede Zeile einer Wahrheitstafel mit dem Ausgangswert 0 sind alle Variablen, die sich im logischen Zustand 1 befinden zu negieren. Sie werden mit den Eingangsvariablen im logischen Zustand 0 durch ODER verknüpft.

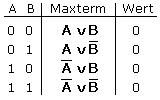
Die vollständige konjunktive Normalform (KNF) mit dem logischen Ausgangszustand 0 besteht aus nur einer Volldisjunktion (ODER-Verknüpfungen) oder mehreren durch UND verknüpften Volldisjunktionen mit dem Ausgangszustand 0. Bei bekannter Wahrheitstafel wird die Schaltnetzfunktion durch UND-Verknüpfungen aller Maxterme mit den logischen 0-Zuständen herausgeschrieben.

• Haben nur wenige Ausgangsvariablen den logischen 1-Zustand, so ist die DNF mit Mintermen die bessere Wahl.
• Haben weniger Ausgangsvariablen den logischen 0-Zustand, so ist die KNF mit Maxtermen geeigneter.

Es genügt mit der disjunktiven Normalform vertraut zu sein, da sie in die konjunktive Normalform umgerechnet werden kann. Dazu wird die DNF im ersten Schritt doppelt negiert. Die Negierungen werden von innen nach außen aufgelöst. Nach De Morgan werden aus ODER-Verknüpfungen der Glieder UND-Verknüpfungen und die Negierungen der Einzelglieder lösen sich auf. Im Folgeschritt werden die Therme unter der gemeinsamen Negierung nach dem Distributivgesetz behandelt. Nach weiteren Vereinfachungen wird im letzten Schritt die verbliebene Gesamtnegierung nach De Morgan aufgelöst.

Leider nimmt der Rechenaufwand bei mehr Eingangsvariablen sehr schnell zu. Einfacher ist es aus der Wahrheitstafel die benötigte KNF oder DNF herauszuschreiben.