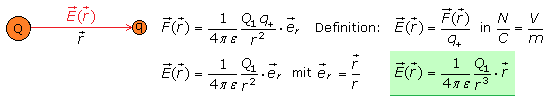Statisches elektrisches Feld
Dieses Kapitel beschreibt das homogene elektrostatische Feld, das elektrische Potenzial, die Potenzialdifferenz und Spannung und stellt vereinfacht vektorielle Eigenschaften des elektrischen Felds dar. Elektrische Ladungen sind an Materie gebunden und treten in ganzzahligen Vielfachen der Elementarladung e = 1,6·10(exp −19) C auf. Es wird zwischen positiven und negativen Ladungen unterschieden.
Die Einheitenbezeichnung Coulomb ist die zu Ehren des französischen Physikers C. A. Coulomb abgeleitete SI-Einheit der elektrischen Ladung. 1 C ist die elektrische Energie, die der übertragenen Ladung entspricht, die innerhalb einer Sekunde durch einen konstanten elektrischen Strom von 1 A erbracht wird.
In einem aus dem Physikunterricht bekannten Versuch wird ein Plattenkondensator von einer Hochspannungsquelle aufgeladen. Die eine Platte hat eine positive und die andere den gleichen Betrag an negativer Ladung. Hängt man in die Mitte dieser Platten eine kleine positiv oder negativ aufgeladene Masse, so wird sie von der entgegengesetzt geladenen Platte angezogen. Kommt es zur Berührung, so bewegt sich der kleine Probekörper zur gegenüberliegenden Platte. Nach dem Berühren fliegt der Probekörper solange hin und her, bis der Hochspannungsgenerator abgeschaltet wird. Zwischen den Kondensatorplatten muss es eine Kraft geben, die auf den Probekörper wirkt.
Das mechanische Äquivalent ist die Anziehungskraft der Erde auf eine hochgehobene kleine Masse, die beim Loslassen zur Erde zurückfällt. Ein etwas anspruchsvollerer Versuch ist die Gravitationswaage mit zwei feststehenden großen Bleikugeln und einem dazwischen drehbar aufgehängten Balken mit zwei kleinen Bleikugeln. Nach Freigabe des Balkens bewegen sich die Massen aufeinander zu, da die großen Bleikugeln mit ihrer höheren Gravitationskraft eine größere Wirkung auf die kleinen Massen ausüben. Zwischen den Kugeln besteht ein Gravitationsfeld mit einer Gravitationsfeldstärke.
Zwischen den elektrisch unterschiedlich, beim Plattenkondensator genau gegensätzlich aufgeladenen Platten besteht ein elektrisches Feld. Der Versuch zeigt, dass die positive Probeladung von der negativ geladenen Platte angezogen wird. Beim Berühren kommt es dort zum Ladungsausgleich und ein kleiner Teil des Ladungsüberschusses der Platte wird auf den Probekörper übertragen. Da der Körper beweglich aufgehängt ist, stoßen sich die gleichartigen Ladungen ab. Gleichzeitig zieht die positive Platte den nunmehr negativ geladenen Probekörper an. Die elektrische Feldstärke zwischen den Platten, die für die Bewegung des Probekörpers erzeugt, ist direkt von der Ladungsmenge auf den Platten abhängig. Die Kraft, die auf eine Probeladung einwirkt, ist direkt von der Feldstärke abhängig.
Kann der geladene Probekörper keine der Platten berühren, wo wird er von der gegenteilig geladenen Platte angezogen und entsprechend von der gleichartig geladenen Platte abgestoßen. Die Auslenkung ist umso stärker, je mehr Ladungen sich auf den Kondensatorplatten befinden, die dadurch ein stärkeres elektrisches Feld erzeugen. Wird das äußere Feld abgeschaltet, dann wird der Probekörper nach keiner Seite ausgelenkt, seine eigene Ladung bleibt aber erhalten.
Elektrisch geladene Körper üben Kräfte aufeinander aus. Die Kraftwirkung ist proportional zur Ladungsmenge und nimmt mit zunehmender Entfernung zur Ladungsquelle ab. Versuche zeigen, dass sich gleichnamig geladene Körper abstoßen und ungleichnamige Ladungen anziehen.
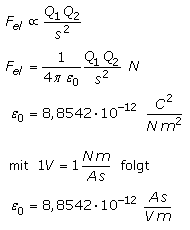
Die von einer ortsfesten Ladung ausgehende Kraftwirkung wird mit einer kleinen frei beweglichen Ladungssonde gemessen. Diese bewegliche Probeladung ist definiert als sehr kleine, punktförmige, positiv geladene Kugel und frei von Masseanziehungskräften. Die Kraftwirkung elektrischer Ladungen wird durch das hergeleitete Coulombgesetz beschrieben. In der Proportionalitätskonstante ist die elektrische Feldkonstante εo (epsilon, griech. Kleinbuchstabe) enthalten. Sie besagt, dass eine Kraftvermittlung auch im Vakuum besteht und keines stofflichen Mediums bedarf.
Wirkt die Kraft nicht direkt, sondern durch einen elektrisch nicht leitenden Stoff hindurch, muss mit einer weiteren Permittivitätszahl εr korrigiert werden. Dividiert man die Coulombkraft Fel durch die Probeladung, so wird man von ihrer Größe unabhängig. Man erhält einen normierten Ausdruck, der das elektrische Feld E beschreibt. Die elektrische Feldstärke ist die Kraft, die ein statisches elektrisches Feld in einem bestimmten Raumpunkt auf eine dort befindliche positive elektrische Ladung von 1 A·s ausübt.
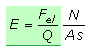
Jede elektrische Ladung ist von einem Kraftfeld umgeben. Kraftwirkung und Richtung können durch Feldlinien dargestellt werden. Je stärker ein elektrisches Feld ist, desto mehr Feldlinien muss man sich pro Flächeneinheit vorstellen, die Feldliniendichte ist größer. Im Experiment richten sich Farnsporen oder feinste Kunststofffasern entlang der Feldlinien aus. Ein gerichtetes Feld wird Vektorfeld genannt. Die Feldstärke kann an jedem Ort durch einen Pfeil dargestellt werden. Er zeigt in die Feldrichtung und gibt mit seiner Länge die Betragsgröße der Kraft an diesem Ort an. Die Feldlinien beginnen und enden auf Ladungen. Per Definition treten sich rechtwinklig aus positiven Ladungen aus und enden mit rechtwinkligem Auftreffen auf negativen Ladungen. Feldlinien kreuzen sich nie. Das folgende Bild zeigt inhomogene Felder elektrischer Ladungen und deren stilisierten Feldverlauf. Das elektrische Feld variiert in Stärke und Richtung.
Das statische elektrische Feld ist ein Quellenfeld. Die positive Ladung ist als Quelle und die negative Ladung als Senke definiert. Die Kraftrichtung kann für jeden Punkt des elektrischen Feldes durch Zeichnen der Tangente in diesem Punkt an die Feldlinie angegeben werden. Die Richtung der Tangente stimmt mit der Richtung der elektrischen Feldgröße überein. Die Feldstärke am Bestimmungsort ist proportional zur dort bestehenden Feldliniendichte.
△Homogenes elektrostatisches Feld
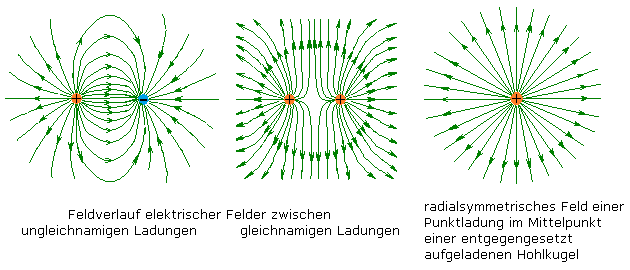
Zwei zueinander parallel ausgerichtete Metallplatten, die kurzzeitig mit einer Spannungsquelle verbunden waren, haben danach ein zwischen den Platten messbares elektrisches Feld. Da die Platten gegeneinander isoliert sind, gibt es keinen Ladungstransport und die Ladespannung bleibt erhalten. Parallel zu den Platten ist in jedem Abstand eine konstante Feldstärke messbar. Nahe den Plattenrändern gilt das nicht mehr.
Das Kennzeichen eines elektrostatischen Feldes sind ruhende Ladungen.
Es fließt kein elektrischer Strom und somit entsteht kein Magnetfeld.
Die Feldlinien sind rotationsfrei, sie beginnen auf positiven und enden auf negativen Ladungen.
Im homogenen Feld verlaufen die Feldlinien parallel zueinander. Die Feldliniendichte ist konstant.
Verursacht wird das elektrostatische Feld durch das Anlegen einer Gleichspannung an die Platten. Da die Kondensatorplatten gegeneinander isoliert sind, ist der Stromkreis nicht geschlossen und es sollte eigentlich kein Strom fließen. Die am noch ungeladenen Kondensator angeschlossene Gleichspannungsquelle kann mit ihren Polen als äußeres elektrostatisches Feld aufgefasst werden. Die metallischen Kondensatorplatten besitzen als elektrische Leiter freie bewegliche negative Ladungsträger. Sie werden vom positiven Pol der Spannungsquelle angezogen und vom negativen Pol abgestoßen.
Die Spannungsquelle bewirkt eine Verschiebung der Ladungsträger in den Leitungen und den Platten. Eine Platte lädt sich positiv und die andere entsprechend negativ auf. Der Lade- und Verschiebestrom fließt so lange, bis zwischen der Ladespannung und dem elektrischen Feld ein Gleichgewicht entstanden ist.
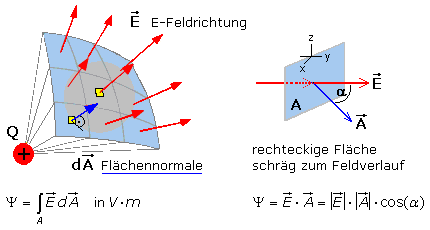
Elektrischer Fluss
Die an den Kondensator angelegte elektrische Spannung bewirkt zwischen den Kondensatorplatten den elektrischen Fluss Ψ (Psi, griech. Buchstabe), auch Verschiebungsfluss genannt. Er entspricht der Zahl der Feldlinien und ist gleich der elektrischen Ladung des Körpers. Der elektrische Fluss transportiert keine Ladungsträger. Zur Berechnung gilt: Ψ = C · U, mit der Einheit A·s.
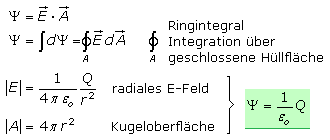
Flussdichte
Der elektrische Fluss eines geladenen Körpers der eine geschlossene Fläche senkrecht durchsetzt erzeugt die Flussdichte D. Sie ist somit gleich der Ladungsdichte und proportional zur Feldstärke. Zur Berechnung gelten: D = Ψ / A = Q / A und D0 = ε0 · E
Ist der Radius einer elektrisch geladenen Fläche klein, dann herrscht dort bei hoher Ladung eine hohe elektrische Feldstärke und zu einem nahen Flächenelement eine große Flussdichte. In Gewitternähe lassen sich daher an leitenden metallischen Spitzen Elmsfeuer als Corona- oder Spitzenentladungen beobachten.
Permittivität
Das elektrische Feld wirkt im Vakuum und durchdringt elektrische Isolatoren. Bei konstant gehaltener Feldstärke ist die Flussdichte vom Isolationsmaterial im E-Feld abhängig. Die Permittivität ε oder dielektrische Leitfähigkeit ist das Produkt der elektrischen Feldkonstanten und einer materialabhängigen dimensionslosen Permittivitätszahl. Sie gibt an, wie viel Mal größer die elektrische Flussdichte ist, wenn statt Vakuum ein anderes Isolationsmaterial verwendet wird. Für Luft ist in sehr guter Näherung εr = 1. Fast immer ist εr auch noch von der elektrischen Feldstärke abhängig.
Influenz
Zur Darstellung der Influenz bringt man in einem Laborversuch in einen großen elektrisch geladenen Plattenkondensator zwei weitere noch leitend zusammenliegende Platten ein. Das elektrische Feld des Kondensators verschiebt die frei beweglichen Elektronen in den eingebrachten Metallplatten und lädt deren Oberflächen dem äußeren Feld entgegengesetzt auf. Werden die Metallplatten mechanisch getrennt, bilden sie einen weiteren kleinen Kondensator mit entgegengesetztem Feldverlauf. Der Raum zwischen den neuen Kondensatorplatten ist Feld frei. Die Spannung über dem großen Kondensator nimmt dadurch ab.
Nimmt man die getrennten Platten aus dem großen Kondensator heraus, entspricht sein Feld wieder dem anfänglichen Zustand. Auf dem kleinen Kondensator hat man durch Ladungsverschiebung, der Influenz, eine Ladung ΔQ = D · A erzeugt und durch mechanische Energiezufuhr getrennt. Er hat ein eigenes elektrisches Feld und an ihm kann eine Spannung gemessen werden.
Wird nur eine von zwei isoliert aufgehängten Metallkugeln elektrisch positiv oder negativ aufgeladen, so ziehen sich die beiden Kugeln an. In der zuvor elektrisch neutralen Metallkugel werden die relativ frei beweglichen Elektronen durch das E-Feld der anderen Kugel so verschoben, dass sich die dem Feld zugewandte Seite durch Influenz entgegengesetzt auflädt. Zwischen den ungleichen Ladungen wirkt die Coulombkraft.
Influenz ist Ladungstrennung, die auf einem Leiter im elektrischen Feld stattfindet.
Die Ladung wird so lange verschoben, bis die Feldstärke im Leiterinnenraum zu null wird.
An der Leiteroberfläche ist die Influenzladung dem äußeren Feld entgegengerichtet.
Dielektrische Polarisation
Wirkt das elektrische Feld auf einen Isolator, so kann keine Ladungstrennung wie bei der Influenz erfolgen. Im Isolator gibt es keine freien Elektronen. Die Ladungszentren der Elektronenhüllen um Atome und Moleküle können teilweise durch das Feld verformt und somit polarisiert werden. Die dipolähnlichen Strukturen richten sich dann entsprechend ihrer Ladungsverteilung entlang der Feldlinien aus. Der Vorgang wird Verschiebungspolarisation genannt. Von Orientierungspolarisation spricht man, wenn das Dielektrikum, der Isolator selbst schon Dipolcharakter hat.
△Potenzial, Spannung als Potenzialdifferenz
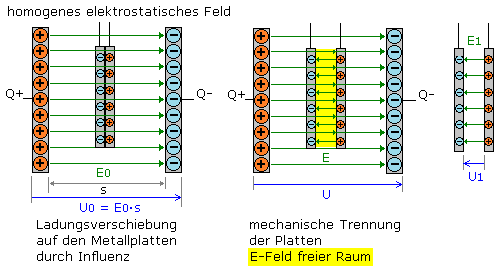
Ausführliche mathematische Betrachtungen zum elektrischen Feld und seinen Größen findet man im letzten Kapitel dieser Seite. Jedem Ort, wo sich eine elektrische Ladung befindet, kann ein bestimmtes elektrisches Potenzial φ zugeordnet werden. Der Wert hat die Benennung Joule/Coulomb = Volt. Es gibt an, wie groß die potenzielle Energie einer Probeladung q ist, die aus dem Unendlichen oder vom Nullpotenzial an diesen Ort des Felds gebracht wird. Die elektrische potenzielle Energie errechnet sich aus dem Transport einer Probelladung q an einen Ort im Quellenfeld Q. Das Verbinden aller Punkte gleichen Potenzials ergibt die Äquipotenziallinien. Sie werden von den Feldlinien immer senkrecht geschnitten. Im räumlichen Feld führt das Verbinden der gleichen Äquipotenziallinien zur Äquipotenzialfläche. Im homogenen E-Feld ist die Bezugslinie oder Ebene der negativen Ladungen als Nullpotenzial definiert. Im inhomogenen E-Feld liegt das Nullpotenzial vom Ursprung der Quellenladung Q ausgehend radialsymmetrisch entfernt im Unendlichen.
Äquipotenziallinien sind Linien gleichen Potenzials (Energiegehalts).
Feldlinien und Äquipotenziallinien stehen immer senkrecht aufeinander.
Betrachtung für das homogene elektrische Feld
Wird im dargestellten homogenen E-Feld die positive Probeladung q vom Nullpotenzial nach oben zur positiven Ladung Q bewegt, muss eine äußere Kraft die zunehmende Abstoßungskraft zur positiven Ladung Q überwinden. Die potenzielle Energie der Probeladung q nimmt zu. Wird sie im homogenen E-Feld links oben losgelassen, wirkt eine Kraft Fel in Feldrichtung und beschleunigt sie entlang der Feldlinien um die Wegstrecke Δs. Die potenzielle Energie der Probeladung nimmt ab und ihre kinetische Energie zu. Die Ladung bewegt sich in das Gebiet mit geringerer potenzieller Energie und verrichtet elektrische Arbeit Wel. Die durchlaufene Potenzialdifferenz ist das Maß der Arbeit und wird als elektrische Spannung U bezeichnet.

Auf dem Weg von φ1 nach φ2 verliert die Probeladung potenzielle Energie. Die Berechnung der Potenzialdifferenz U21 zeigt mit dem Minuszeichen, dass am Ende das Potenzial bei φ2 niedriger ist. In elektronischen Schaltungen wird die Spannung meistens in Bezug zum Nullpotenzial also als U12 gemessen. Der Wert ist dann wie zu erwarten positiv.
Die Spannung ist positiv, wenn die Ladungsbewegung in Richtung des elektrischen Felds erfolgt.
Im homogenen elektrischen Feld, das im Zwischenraum entgegengesetzter Ladungen eines Plattenkondensators angenommen werden kann, ist der Betrag der Feldstärke |E| konstant, proportional zur Ladungsmenge Q und umgekehrt proportional zur Plattenfläche. Dieses Ergebnis folgt aus der Kombination einiger weniger elektrotechnischer Formel. Ein (Platten)-Kondensator wird auf eine Spannung U aufgeladen und die Spannungsquelle abgetrennt. Wird der Plattenabstand vergrößert, dann nimmt die Spannung des geladenen Kondensators zu, wobei die anfangs erfolgte Ladungsverschiebung Q nicht verändert wird. Die Kapazität C des kondensators ist umgekehrt proportional zum Plattenabstand d. Für den zu betrachtenden Fall bleibt auch die Plattenfläche A konstant.

Betrachtung für das inhomogene elektrische Feld
Per Definition gilt für das inhomogene Radialfeld einer Ladung, dass die potenzielle Energie in unendlicher Entfernung gegen null strebt. Bringt man eine Probeladung aus dem Unendlichen in das Quellenfeld ein, dann erfährt sie an jedem Ort eine Kraft, für die das Coulombgesetz gilt. Da es sich um ein konservatives elektrisches Kraftfeld handeln soll, ist die verrichtete Arbeit vom Weg unabhängig und auf geschlossener Wegstrecke null. Es kann also für jeden Ortspunkt die potenzielle Energie bestimmt werden, die eine dort befindliche Ladung hätte.

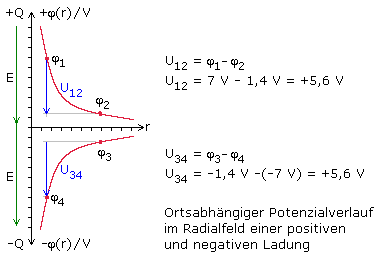
Die grafische Darstellung φ = f(r) ergibt eine Hyperbel. Das Potenzial φ(r) ist proportional zur Quellenladung und umgekehrt proportional zum Abstand des Ladungszentrums. Die Feldlinien verlaufen von positiver zu negativer Ladung. Die Spannung in Feldrichtung ist positiv.
Elektrisches Feld der Erde
Die Erde besitzt ein elektrisches Radialfeld mit senkrecht zur Erdoberfläche weisenden Feldlinien. Zwischen ihr und der leitenden Ionosphäre in rund 80 km Höhe beträgt die durchschnittliche Ladungsdifferenz um 0,5 ... 0,6 MC. Die Erdoberfläche ist als negativ geladen definiert. Zwischen der Erdoberfläche und der Ionosphäre lassen sich im Mittel rund 300 kV ermitteln. Wird die Ionosphäre als positiv geladene Kugeloberfläche und die Erde dazu als zentrisch angeordnete innere Kugelfläche gesehen, dann ist die Lufthülle das Dielektrikum und dient als Isolator. Das System entspricht einem Kugelkondensator mit der Kapazität von rund 1,7 Farad.
In Bodennähe kann zwischen der Erdoberfläche und Atmosphäre eine durchschnittliche elektrische Feldstärke von 100 ... 150 V/m gemessen werden. Die geringe Leitfähigkeit der Luft sorgt für Ladungsverluste des Felds, die aber stetig ausgeglichen werden. Für den Ladungserhalt sorgen unter anderem kosmische Strahlung, radioaktiver Zerfall und die Ladungstrennung, die bei Reibung zwischen kleinen Teilchen bei der Windverfrachtung in der Atmosphäre ersteht. Die idealisiert kugelförmige Oberfläche der Erde errechnet sich zu 5,1·10^14 m². Mit einer mittleren Feldstärke von 130 V/m ist beträgt die absolute Kugelladung die im Absatz oben aufgerundet angegebenen 0,6 MC.
△