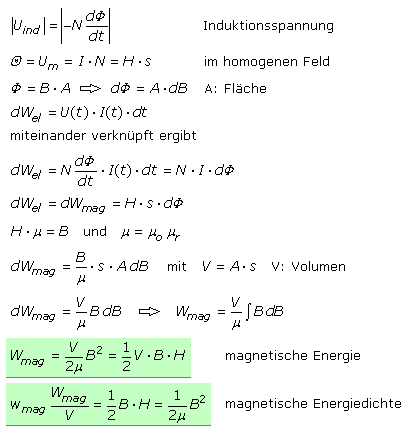Physikalische Größen eines Magnetfelds

Im Folgenden werden wichtige physikalische Größen des Magnetfelds beschrieben und Eigenschaften des magnetischen Kreises mit denen des elektrischen Kreises verglichen. Abschließend gibt es Hinweise zur Energie eines Magnetfelds und zur Kraft, die von einem Magnetpol ausgeht. Die Betrachtungen gelten für die Magnetostatik.

Die Durchflutung

Nach dem Anlegen einer Spannung bewegen sich die freien Elektronen im Leiter entlang der elektrischen Feldlinien als elektrischer Strom vom Minus- zum Pluspol. H. Christian Ørsted beobachtete 1820, dass ein vom Strom I durchflossener elektrischer Leiter von einem Magnetfeld umgeben ist. Dieses Magnetfeld ist von der Flussrichtung und der Stromstärke abhängig. Mit Magnetnadeln oder Eisenpulver kann gezeigt werden, dass der Leiter vom Magnetfeld konzentrisch umgeben ist. Die sich bewegenden Elektronen durchfluten auf ihren Strompfaden das von ihnen erzeugte Magnetfeld. Die Durchflutung hat eine auf das Leiterinnere bezogene und außerhalb des Leiters messbare Komponente.

Die Durchflutung hat das Formelzeichen Θ (Theta, griech. Großbuchstabe) mit der Einheit Ampere. Im Elektromaschinenbau werden teilweise Amperewindungen (Aw) als Benennung verwendet. Die Durchflutung ist das Produkt aus der Stromstärke und der Windungszahl: Θ = I · N in Ampere.

Die Stromdichte ist die Summe aller Strompfade, die durch ein Flächenelement gehen, das von einer geschlossene Kurve umgeben ist. Die Stromdichte ist die Ursache für das Magnetfeld. In Analogie dazu ist beim geschlossenen Stromkreis die Spannung die Ursache für den Strom. Die magnetische Durchflutung wird auch als magnetische Spannung Um bezeichnet und ist das Maß für die Kraft, die von der magnetischen Feldstärke H ausgeht.

Magnetische Feldstärke

Die magnetische Feldstärke hat das Formelzeichen H mit der Einheit (A/m). Diese Größe kann mathematisch berechnet aber nicht direkt gemessen werden. Gemessen wird die später beschriebene magnetische Flussdichte B. Fließt durch einen geraden unendlich lang angenommenen Leiter der Strom 1 A, so ist im gleichbleibenden Abstand von 1 m zum Leiter an jeder Stelle des Raums die magnetische Feldstärke H = 1 A/m.

Die folgenden Betrachtungen gelten für Gleichstrom und für Ströme mit Frequenzen kleiner 1 MHz. Die magnetische Feldstärke außerhalb eines Leiters ist umgekehrt proportional zum Leiterabstand. Vereinfacht angenommen fließt der Strom zentriert und homogen verteilt durch den Leiter. Die magnetische Feldstärke H entlang einer geschlossenen Umfangslinie, hier dem Kreisumfang ist konstant. Der wirksame Strom ist die Summe aller gerichteten Strompfade, die die umrandete Fläche durchfluten. Jedes freie Elektron im Leiter, das dem angelegten E-Feld (Spannung) folgt, bildet einen Strompfad, der konzentrisch vom Magnetfeld umgeben ist. Im Leiter kann jede geschlossene Umlauflinie gewählt werden, wobei nur die davon eingeschlossenen Strompfade einen Beitrag zur Durchflutung liefern. Das Magnetfeld außerhalb des Leiters ist die Summe aller Teilmagnetfelder der Strompfade im Leiter. Diese Stromsumme I bewirkt, dass direkt entlang des Leiterumfangs die magnetische Feldstärke ihren höchsten Wert hat. Sie nimmt mit der Entfernung vom Leiter ab.

Mathematisch und wissenschaftlicher beschrieben wird das Durchflutungsgesetz oder Ampèresche Gesetz durch das Linienintegral der magnetischen Feldstärke H entlang eines in sich geschlossenen räumlichen Integrationswegs (Kurve, Kontur). Im Leiterinnenraum ist das Ergebnis gleich dem Flächenintegral aller Strompfade (Vektor J) innerhalb der Fläche, die vom Integrationsweg umschlossen wird. Der Normal(en)vektor der Flächen ist in Stromrichtung orientiert. Die gerichteten Größen werden mathematisch als Vektoren behandelt. Die Herleitung erfolgt hier für den einfachen Fall einer Kreiskontur. Auf dem Kreisumfang ist die Feldstärke H für jeden Wegabschnitt (ds) konstant.

Das Skalarprodukt ist das Produkt der Vektorbeträge. Der geschlossene Integrationsweg als Summe aller Wegabschnitte soll gleich dem Kreisumfang sein. Der Strom soll sich im Leiter homogen verteilen. Durch jedes differentielle Flächenelement fließt der gleiche Teilstrom. Die Stromdichte im gesamten Flächenelement, das von der Wegkontur, hier dem Kreisumfang umschlossen ist, ist gleich dem Gesamtstrom I. In der Skizze ist R der Leiterradius. Bei der Betrachtung von Kreiskonturen innerhalb des Leiters wird der Radius ri verwendet. Innerhalb des Leiters nimmt die magnetische Feldstärke H(ri) vom Zentrum bis zum Leiterrand proportional mit dem Abstand zu. Entlang des Leiterrands erreicht sie ihren höchsten Wert. Außerhalb des Leiters nimmt H(r) umgekehrt proportional mit dem Abstand ab.

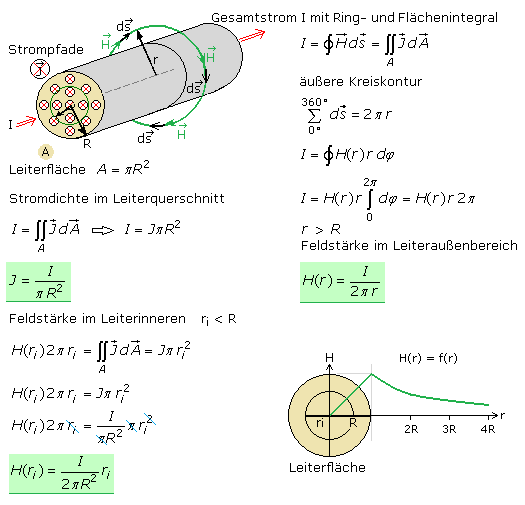
Wird der Leiter zum Leiterring und fortlaufend zur Spule geformt, dann nimmt die Durchflutung bei gleichem Strom I proportional mit der Zahl N der Leiterschleifen zu. Wird bei gleicher Durchflutung Θ der Durchmesser des Leiterrings oder der Spule verkleinert, so liegen die Magnetfeldlinien näher beieinander. Die Feldstärke nimmt zur Ringmitte hin zu. Bei mehrlagig gewickelten Spulen und Kreisringspulen wird in guter Näherung die Feldstärke entlang des mittleren Abstands lm zum Spulenzentrum berechnet.

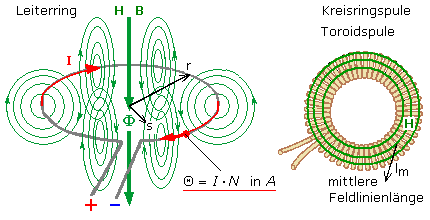
Der Feldlinienverlauf eines Leiterrings ist nicht homogen. Die Bestimmung von H erfolgt mit dem Ringradius r und dem Abstand s vom Ringmittelpunkt. Bei einer Zylinderspule ist neben der Windungszahl N die Länge l der Spule und der Durchmesser der Windungen zu berücksichtigen. In einer langen Zylinderspule verlaufen in guter Näherung die Feldlinien homogen und parallel zueinander. Ist die Spulenlänge im Vergleich zur Windungsfläche sehr groß, dann ist das magnetische Feld vom Abstand der Flächenmitte nahezu unabhängig. In der Spulenmitte ist H am höchsten und nahe den beiden Enden halb so groß.

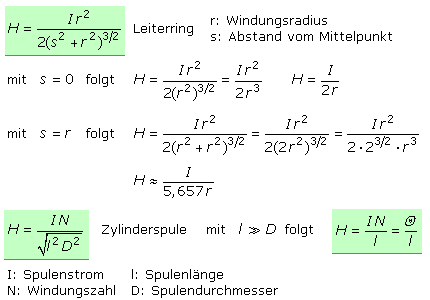
Magnetischer Fluss

Mit dem magnetischen Feld H ist der magnetische Fluss verbunden. Er ist eine skalare Größe, und kann positiv oder negativ sein. Der magnetische Fluss ist ein Maß für die Anzahl der magnetischen Feldlinien H eines Permanent- oder Elektromagneten, die durch eine im Feld angenommene Fläche gehen. Er ist proportional zur Feldstärke H und zur Fläche innerhalb des Feldes. Das Formelzeichen ist Φ (Phi, griech. Großbuchstabe) mit der Einheit (V·s) oder Weber (Wb) zu Ehren des Physikers Weber.

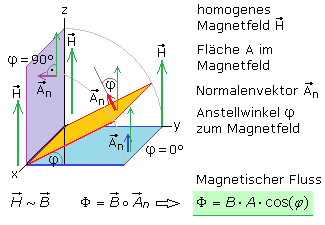
In der Skizze befindet sich die Ausgangsfläche A in der x-y-Ebene. Die Feldrichtung verläuft senkrecht dazu in z-Richtung. Der Normalenvektor An einer Fläche steht immer senkrecht auf der Fläche. Für die blaue Fläche zeigt er in Feldrichtung und der Anstellwinkel φ beträgt 0°. Diese Fläche umschließt die maximale Anzahl der Feldlinien. Wird diese Fläche um 90° gedreht, so steht sie als violette Fläche parallel zur Feldrichtung. Der Normalenvektor der Fläche bildet mit der Feldrichtung den Winkel 90°. In dieser Stellung erfasst die Fläche keine Feldlinien. Der magnetische Fluss ist proportional zum Kosinus des Anstellwinkels φ. Er wird von den Vektoren der Feldrichtung und dem Normalenvektor aufgespannt. Die effektiv wirksame Fläche ist die senkrechte Projektion der um φ gedrehten Fläche auf die Ausgangsfläche. Der magnetische Fluss ist das Skalarprodukt zwischen dem Feldvektor und dem Flächen-Normalenvektor. Ohne spezielle Vektorrechnung wird das Produkt aus dem Wert der Feldstärke, der Fläche und dem Kosinus des Anstellwinkels φ gebildet.

Magnetische Flussdichte

Ein elektrischer Leiter der Länge s soll sich in einem äußeren Magnetfeld H befinden und vom elektrischen Strom I durchflossen werden. Das vom Leiter erzeugte magnetische Feld überlagert sich mit dem äußeren Feld. Auf den Leiter wird eine Kraft ausgeübt, die proportional zum Strom I und der Leiterlänge s ist, die sich im äußeren Feld befindet. Sich frei bewegende elektrische Ladungen entsprechen einem elektrischen Strom und werden ebenso von einwirkenden äußeren Magnetfeldern beeinflusst. Beispiele dazu sind die Braunsche Röhre früherer Fernsehgeräte und Oszilloskope und die Fadenstrahlröhre, mit der im Physiklabor die Ablenkung eines Elektronenstrahls durch Magnetfelder sichtbar gemacht wird.

Die Definition der Proportionalitätskonstanten, der magnetischen Flussdichte B, führt zu Gleichungen für die Berechnung der Kraft auf bewegte Ladungen im einwirkenden Magnetfeld. B ist eine vektorielle Größe, die der Kraft des H-Felds entspricht. Im Vakuum sind die beiden vektoriellen Feldgrößen H und B zueinander proportional. Die Proportionalitätskonstante ist die magnetische Feldkonstante des Vakuums μo, die auch als magnetische Permeabilität bezeichnet wird. Die maximale magnetische Flussdichte B, auch magnetische Induktion genannt, gibt die Dichte der magnetischen Feldlinien durch eine senkrecht zur Feldrichtung liegenden Fläche an. Das Formelzeichen ist B, eine vektorielle Größe mit der Einheit (V·s/m²) oder (T), zu Ehren des Physikers Tesla.

Die Vektorgröße B zeigt in die Richtung der magnetischen Feldgröße H. Die magnetische Kraftwirkung Fmag errechnet sich mithilfe des Vektorprodukts aus B und der Bewegungsrichtung. Schließen beide Vektorgrößen einen rechten Winkel ein, so steht der Kraftvektor Fmag senkrecht zu beiden Ausgangsvektoren. Das Vektorprodukt für beliebige Winkel errechnet sich aus den Längen der Ausgangsvektoren multipliziert mit dem Sinus des aufgespannten Winkels. Die maximale Kraftwirkung entsteht beim 90° Winkel, da sin(90°) = 1 ist. Die magnetische Kraft auf bewegte Ladungen ist die Lorentzkraft.

Magnetische Permeabilität

Die magnetische Feldkonstante des Vakuums μo ist der Quotient der magnetischen Flussdichte B zur magnetischen Feldstärke H und kann mithilfe mehrerer Naturkonstanten hergeleitet werden. Auch für eine Spule ohne Kern (Luftspule) gilt praktisch dieser Wert. Wird das Kernmaterial geändert, so kann sich das Verhältnis B/H bei konstant gehaltener Magnetfeldstärke mehr oder weniger stark ändern. Die relative Permeabilität oder Durchlässigkeit für Magnetfeldlinien μr ist eine dimensionslose Zahl und für Kernwerkstoffe sehr unterschiedlich. Auch für denselben Kernwerkstoff variiert μr oft nicht linear mit der magnetischen Feldstärke und durchläuft einen Sättigungswert. Magnetisierbare Legierungen aus Eisen, Kobalt und Nickel haben die Fähigkeit magnetische Feldlinien in sich zu konzentrieren und verstärken das Magnetfeld. Blei, Zinn und Kupfer können magnetische Feldlinien geringfügig verdrängen und das Magnetfeld etwas schwächen. Für die magnetische Flussdichte einer Spule mit Kern gilt die Formel: B = μo · μr · H

Die Permeabilitätszahl μr eines Stoffes gibt an, wie viel Mal größer die magnetische Flussdichte B gegenüber Vakuum oder Luft bei gleicher Durchflutung Θ ist.
Die Permeabilität μ ist das Produkt aus der magnetischen Feldkonstante µo und einer dimensionslosen Permeabilitätszahl µr.
Es gilt: μ = μo · μr
Bei diamagnetischen Stoffen ist μr <1. In ihrem Inneren wird ein Magnetfeld gering geschwächt.
Bei paramagnetischen Stoffen ist μr >1. In ihrem Inneren wird ein Magnetfeld gering verstärkt.
Bei ferromagnetischen Stoffen ist μr »1. Sie verdichten die Feldlinien im Inneren und verstärken das Magnetfeld um ein Vielfaches.

Die folgenden Tabellen zeigen durchschnittliche Permeabilitätszahlen verschiedener Werkstoffe.

Die folgende Gegenüberstellung zeigt die wichtigsten Gemeinsamkeiten und Unterschiede zwischen dem statischen elektrischen Feld und dem Magnetfeld.

Magnetischer Kreis

Magnetfeldlinien haben keinen Anfang und kein Ende und bilden ein in sich geschlossenes Wirbelfeld. In Analogie zum geschlossenen elektrischen Stromkreis mit sich bewegenden Elektronen wird der Weg der magnetischen Feldlinien als magnetischer Kreis bezeichnet. Verschiedene Materialien leiten Magnetfeldlinien unterschiedlich gut. In Anlehnung an den ohmschen Widerstand im elektrischen Stromkreis wird ein magnetischer Widerstand im magnetischen Kreis definiert.

Im elektrischen Stromkreis ist die Spannung die Ursache für den Stromfluss. Das Magnetfeld eines Elektromagneten wird von der Durchflutung der Erregerspule aufgebaut, die folglich als Ursache des Magnetfelds als magnetische Spannung bezeichnet wird. Die elektrische Spannung verursacht den elektrischen Strom, entsprechend erzeugt das Magnetfeld den magnetischen Fluss.

Die Tabelle zeigt in einer vergleichenden Gegenüberstellung sich entsprechende Größen des elektrischen und magnetischen Kreises. In den Gleichungen stehen s für die Länge des Leiters oder mittlere Magnetlinienlänge und A für die Fläche. Die Einheit Weber (Wb) entspricht (V·s) im physikalischen SI-Einheitensystem.

In den Baugruppen der Elektrotechnik gibt es magnetische Kreise mit und ohne Luftspalt. Luft ist ein schlechter magnetischer Leiter. In ferromagnetischen Werkstoffen werden die Feldlinien konzentriert hindurch geleitet. Sie zählen zu den besten magnetischen Leitern. Sollen Magnetfeldlinien einen magnetischen Widerstand Rm überwinden, so muss Energie zugeführt werden. Ist der magnetische Fluss bekannt, dann kann der magnetische Kreis berechnet werden. Die Formel Θ = Φ · Rm darf keinesfalls nach Φ umgestellt werden, denn Φ ≠ Θ / Rm

Energie eines Magnetfelds

Der elektrische Strom erzeugt mit dem magnetischen Fluss Φ das Magnetfeld der Spule. Im Magnetfeld ist Energie gespeichert, mit der Arbeit verrichtet werden kann. Die magnetische Flussdichte B ist proportional zum magnetischen Fluss, der eine bestimmte Fläche durchsetzt. Der Proportionalitätsfaktor ist die Fläche A. Das Magnetfeld umgibt konzentrisch den elektrischen Leiter und ist senkrecht zur Stromrichtung ausgerichtet. Der elektrische Strom durchflutet somit das Magnetfeld. Die magnetische Durchflutung oder magnetische Spannung ist direkt proportional zum Strom und zur Windungszahl.

Entsprechend der elektrischen Feldstärke E in V/m ist die magnetische Feldstärke H in A/m definiert. Entlang einer beliebigen geschlossenen magnetischen Feldlinie ist die Summe aller Produkte H · Δs gleich der Durchflutung Θ = N · I, die als magnetische Spannung bezeichnet wird. Für ein homogenes Feld vereinfacht sich das zur korrekten Berechnung von Θ notwendige Ringintegral zu: Θ = N · I = H · s. Darin ist s die betrachtete Feldlinienlänge oder Luftspaltbreite. Die Änderung eines Magnetfelds generiert eine entgegen gerichtete Induktionsspannung Uind.

Im ideal definierten Modell einer Spule wird die elektrische Energie vollständig in magnetische Energie umgewandelt. Die Herleitung beschränkt sich auf den Energiegehalt eines homogenen Feldes, das in Kreisringspulen und im geschlossenen Magnetkern einer Spule zu finden ist. Hat der Magnetkern einen schmalen Luftspalt, so ist in guter Näherung auch dort das Magnetfeld homogen. Die magnetische Energie pro Volumeneinheit wird als magnetische Energiedichte wm bezeichnet.

Kraft eines Magnetpols

Ein fixierter Elektromagnet mit einem Joch aus Weicheisen soll einen beweglichen Anker aus Weicheisen parallel zu sich anziehen. Der Spulenstrom erzeugt im Joch den magnetischen Fluss Φ. An den Jochenden entstehen in Abhängigkeit von der Stromrichtung der Nord- und Südpol. Die Feldlinien durchfließen den Anker und magnetisieren ihn. Jetzt stehen sich zwei Magnete mit ungleichnamigen Magnetpolen gegenüber. Durch Verkürzen der Magnetfeldlinien im Luftspalt kann der Energiegehalt des magnetischen Feldes seinen angestrebten Minimalwert erreichen. Der Anker wird mit einer bestimmten Kraft vom Joch angezogen. Die Geometrien der Magnetpole von Joch und Anker sollen gleich sein. Die Herleitung der Kraft bezieht sich auf einen Pol.

Jeder Pol bewegt den Anker mit seiner Zugkraft F um eine kleine Wegstrecke ds auf das Joch zu. Dabei ändert sich die magnetische Energie um dWm. Die Hubarbeit wird der magnetischen Energie entnommen. Mit der Bedingung, dass bei jeder weiteren Wegänderung die magnetische Flussdichte in den Eisenkernen konstant bleibt, ist die Energie um den Anker anzuziehen nur von der Energiedichte im Luftspalt abhängig. Die Energieänderung kann so mit einer Volumenänderung im Luftspalt gleichgesetzt werden. Im Luftspalt ist der Wert für μr = 1. Der Anker wird mit 2·F, der Kraft beider Pole, angezogen.

Die Gleichung gilt universell für jeden Magneten und lässt nicht erkennen, ob die Flussdichte im Spalt von einem Elektro- oder Dauermagneten erzeugt wurde. Jeder stromdurchflossene Leiter ist von einem Magnetfeld umgeben. Magnetische Kräfte auf stromdurchflossene Leiter sind besonders dann nicht zu vernachlässigen, wenn sehr hohe Ströme in nahe zusammenliegenden Leitern fließen.