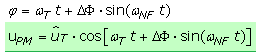Phasenmodulation
Die Phasenmodulation ist, wie im Kapitel der Frequenzmodulation angedeutet, der Winkelmodulation zugeordnet. Bei der Frequenzmodulation wurde gezeigt, dass sich der maximale Phasenhub umgekehrt proportional zur Modulationsfrequenz verhält ΔΦ ~ 1 / fNf, und dass sich der maximale Frequenzhub proportional zum maximalen Phasenhub verhält ΔF ~ ΔΦ. Daraus folgt, dass der Modulationsindex η = ΔF / fNf und der Phasenhub einander gleichwertig sind.
Falls für eine konstante NF-Modulationsfrequenz das Winkelmodulationsverfahren angewendet wird, ist es egal, ob das Modulationsprodukt als frequenzmodulierte oder phasenmodulierte Schwingung bezeichnet wird. Aus den Proportionalitäten kann man ersehen, dass bei konstanter fNf der Frequenzhub und der Phasenhub einander proportional sind.
Bei konstanter NF-Frequenz entsprechen sich Frequenzmodulation und Phasenmodulation.
Nur aufgrund der Abhängigkeit von der NF-Frequenz unterscheidet man zwischen Frequenz- und Phasenmodulation. Bei einem FM-Signal ist der Frequenzhub proportional zur NF-Signalamplitude. Er ist unabhängig von der NF-Signalfrequenz. Der Phasenhub nimmt mit zunehmender NF-Frequenz ab. Die Phasenmodulation zeichnet sich dadurch aus, dass sich der Phasenhub proportional zur NF-Signalamplitude verhält und der Frequenzhub mit der NF-Frequenz zunimmt.
Bei der Phasenmodulation verhält sich der Phasenhub proportional zur NF-Signalamplitude, ist aber unabhängig von der NF-Frequenz.
Der Frequenzhub nimmt mit zunehmender NF-Frequenz proportional zu.
In der FM-Rundfunktechnik wird der Nachteil des abnehmenden Phasenhubs zu höheren Frequenzen durch die senderseitige Preemphasis ausgeglichen. Dadurch verfügt das FM-Sendersignal über frequenzmodulierte als auch phasenmodulierte Eigenschaften. Mit einem reinen FM-Modulator kann die Phasenmodulation erzwungen werden. Ein frequenzabhängiges Filternetzwerk vergrößert proportional zur Frequenz die Amplitude des modulierenden Signals, das dann im FM-Modulator die Trägerfrequenz moduliert.
Verdoppelt sich die Eingangsfrequenz am FM-Modulator, so ist der Phasenhub nur noch halb so groß. Wird für diese Eingangsfrequenz die Amplitude des modulierenden Signals verdoppelt, dann verdoppelt sich auch der Phasenhub. Bezogen auf die einfache Frequenz liefert der FM-Modulator ein Modulationsprodukt mit konstantem Phasenhub. Das Ausgangssignal ist ein phasenmoduliertes HF-Signal.
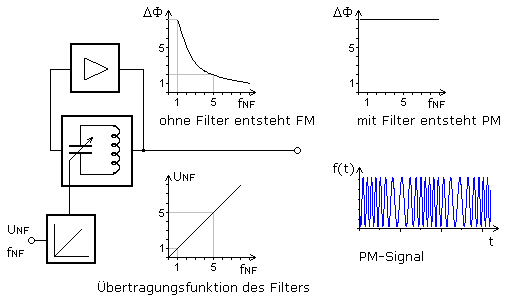
Eine Phasenmodulation entsteht bei der additiven Überlagerung von zwei im Gegentakt stehenden AM-Schwingungen. Die Trägerfrequenz der beiden AM-Signale muss um 90° zueinander phasengedreht sein. Der Summenzeiger weist für den unmodulierten Fall einen Winkel von 45° auf und pendelt bei der Modulation mit dem Phasenhub um diese Lage.
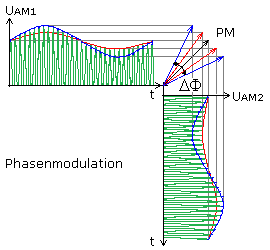
Dieses eher theoretische Verfahren gestattet nur kleine Phasenhübe. Mit größerem Hub erscheinen im Ausgangssignal nicht erwünschte Anteile an Amplitudenmodulation. Das Bild zeigt deutlich, dass der Phasenhub nur von der Nf-Amplitude und nicht von der Frequenz abhängig ist.
Eine weitere angewendete Methode zur Phasenmodulation, aber auch nur für kleine Phasenhübe, arbeitet mit einer konstanten Trägerfrequenz, die quarzstabilisiert sein kann. Dieser Träger wird um 90° phasengedreht und bildet mit der modulierenden NF-Schwingung im Ringmodulator zwei Seitenschwingungen. Das Ausgangssignal ist ein amplitudenmoduliertes Signal mit unterdrücktem Träger. Das ZM-Modulationsprodukt wird additiv mit der nicht phasenverschobenen Trägerfrequenz zum Phasenmodulationssignal überlagert.
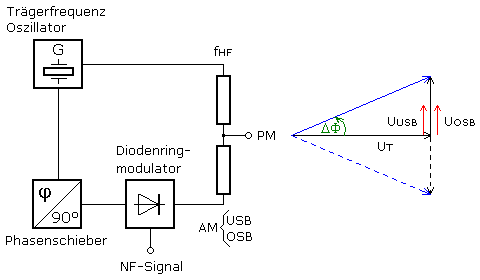
Die mathematische Seite der PM
Im Gegensatz zur Frequenzmodulation wird bei der Phasenmodulation der Winkel direkt moduliert. Der Phasenhub ist unabhängig von der NF-Modulationsfrequenz. Ersetzt man den Phasenhub durch den Modulationsindex η, so ist die Funktionsgleichung identisch mit der für die FM hergeleitete Gleichung.