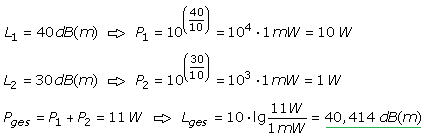Das Dezibel
In der Elektronik werden, besonders oft in der Sende- und Empfangstechnik, Übertragungsfaktoren im logarithmischen Maß angegeben. Die meistens genutzte Bezeichnung ist das Dezibel (dB) und bei der ITU, der internationalen Fernmeldeunion ist gleichberechtigt die Bezeichnung Neper (Np) erlaubt. Es handelt sich um keine echte Einheit wie Volt oder Ampere sondern um eine Pseudoeinheit. Sie weist darauf hin, dass der Zahlenwert aus dem Logarithmus eines Verhältnisses errechnet wurde.
Logarithmen
Der Logarithmus ist nur für positive Zahlen größer null und einer zuvor bestimmten Basis definiert. Jede positive Zahl größer null kann als Potenz einer beliebigen positiven Basis a > 0 und a ≠ 1 geschrieben werden. Die Umrechnung erfolgt mithilfe des Logarithmus. Der dekadische oder Zehner-(Briggsche)-Logarithmus nutzt die Basiszahl a = 10. Im natürlichen Logarithmus ist die Eulersche Zahl e = 2,71828... die Basiszahl. Im Zweierlogarithmus oder binärem Logarithmus ist a = 2.

Berechnungen in der Elektronik werden vorteilhaft mit dem dekadischen Logarithmus durchgeführt, da der Logarithmus einer Zehnerpotenz gleich dem Exponenten ist. Der Zweierlogarithmus ist für den Binärcode der Digitaltechnik geeignet. Berechnungen physikalischer Vorgänge der Natur nutzen oft den natürlichen Logarithmus zur Basis e.
Rechenregeln
Das Multiplizieren und Dividieren unterschiedlicher Größenordnungen wird ebenso wie das Potenzieren und Wurzelziehen durch den Einsatz von Logarithmen erleichtert. Das Rechnen mit Logarithmen reduziert diese Rechenoperation auf eine einfachere Stufe. Aus der Multiplikation wird eine Addition, aus der Potenzrechnung eine Multiplikation. Für das Rechnen mit Logarithmen gelten die folgenden Rechenregeln.
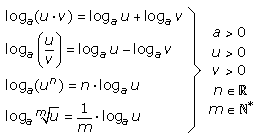
Logarithmen zur Basis a können mit der folgenden Gleichung in eine neue Basis b umgerechnet werden. Für den gegenseitigen Wechsel zwischen Zehner- und natürlichem Logarithmus findet man in Formelsammlungen oft einen Zahlenfaktor.
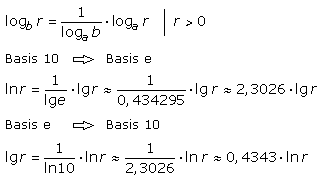
Übertragungsfaktor, Übertragungsmaß und Pegel
Die Anwendung der Logarithmen wird am Beispiel eines Zweitors (Vierpol) gezeigt. Es soll sich um ein lineares System handeln, bei dem ein Eingangssignal verstärkt oder gedämpft als Ausgangssignal erscheint. Zur Vereinfachung soll Leistungsanpassung gelten. Alle Impedanzen sind ohmsche Widerstände und es wird nur Wirkleistung umgesetzt. Die Übertragungsfunktion H ist das Verhältnis der Ausgangsgröße bezogen auf die Eingangsgröße. Nach DIN 40148 war auch das Formelzeichen A für den Übertragungsfaktor möglich. Ist das Verhältnis größer als 1, so entspricht das einem Gewinn G (Gain), gleich einer Verstärkung V (v). Ist das Ergebnis kleiner 1, liegt eine Dämpfung D vor. Sie kann als das Verhältnis der Eingangsgröße zur Ausgangsgröße neu definiert werden oder wird als Kehrwert der Verstärkung geschrieben. Die Verhältnisgrößen sind benennungslose Faktoren.

- Leistungsgröße
- Die Größe ist direkt proportional zur Leistung. Die elektrische Leistung ist das Produkt aus Spannung und Strom und somit eine Leistungsgröße. Die akustische oder Schallleistung ist das Produkt aus dem Schalldruck, der Schallschnelle und der durchschallten Fläche.
- Leistungswurzelgröße
- Das Quadrat der Größe ist proportional zur Leistungsgröße. Bekannt sind sie als Feldgröße, wie elektrische Spannung und Strom, die elektrische und magnetische Feldstärke und ihre Flussdichten sowie in der Akustik der Schalldruck und die Schallschnelle. Fast immer werden sie als Effektivwerte einer sinusförmigen Größe angegeben. Die Angabe der Spitzenwerte oder die Verwendung ihrer komplexen Größe ist ebenso möglich.
- Übertragungsmaß
- Das logarithmische Übertragungsverhältnis wird als Übertragungsmaß bezeichnet. Im SI-Einheitensystem erfolgen die Angaben als Dezibel. Die von der ITU genutzte Angabe in Neper gehört nicht zum SI-System, wird aber toleriert. Die allgemeine Definition der beiden Übertragungsmaße ist unterschiedlich und kann gegenseitig umgerechnet werden.
Neper
Die Pseudoeinheit Neper (Np) basiert auf dem natürlichen Logarithmus mit der Basiszahl e = 2,71828... Die Bezeichnung ist die lateinische Namensform zu Ehren des schottischen Mathematikers John Napier (1550 bis 1617). Neper ist der Einheitenname für den natürlichen Logarithmus des Verhältnisses zweier Energie-, Spannungs-, Strom- und Schalldruckwerte. Traditionell wird das Dämpfungsmaß als Verhältnis der Eingangsgröße zur Ausgangsgröße gebildet. Da die elektrische Leistung das Produkt von Spannung und Strom ist, kann bei konstanten Impedanzen aus dem Verhältnis der Leistungswurzelgrößen recht einfach das Verhältnis der Leistungsgrößen hergeleitet werden.

Dezibel
Der Zehnerlogarithmus auf ein Leistungsverhältnis angewendet ergibt das Leistungsverstärkungsmaß mit der Pseudoeinheit Bel und dem Einheitenzeichen B zu Ehren des amerikanischen Wissenschaftlers Graham Bell. Das Ergebnis ist sehr oft eine Dezimalzahl mit nur einer Vorkommastelle. Um bei Überschlagsrechnungen ohne einen großen Fehler auf Nachkommastellen zu verzichten, wird das Ergebnis mit 10 multipliziert. Das Ergebnis ist ein zehntel Bel und der Einheitenname wird zur Einheitenbezeichnung Dezibel mit dB.
Die Beschreibung einer Übertragungsstrecke erfolgt fast immer für eine vorgegebene Eingangsgröße als Bezugswert und das Übertragungsverhalten wird als Quotient der Ausgangsgröße zur Eingangsgröße angegeben. Bei einem auf Leistung angepassten System mit gleichen Ausgangs- und Eingangsimpedanzen können die Leistungen durch die Quadrate der Ausgangs- und Eingangsspannungen oder Ströme ersetzt werden. Wird ein Exponentialausdruck logarithmiert, so wird der Logarithmus der Basis mit dem Exponenten multipliziert.
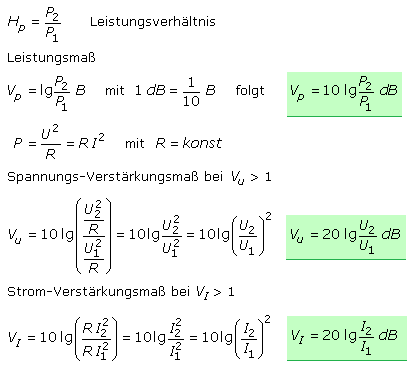
Auch wenn die Ein- und Ausgangsimpedanzen eines Zweitors unterschiedlich sind, können weiterhin die Verhältnisgleichungen benutzt werden. Die direkte Beziehung und Umrechnung zwischen Spannung, Strom und Leistung ist dann nicht mehr gegeben. Bei einem positiven Dezibelwert ist das Ausgangssignal verstärkt und bei negativem dB-Wert gedämpft. Verstärkung und Dämpfung sind zueinander reziprok.
Mit der Umkehrfunktion des Logarithmus können aus den jeweiligen dB-Werten die Verstärkungs- oder Dämpfungsfaktoren errechnet werden. Der dekadische Logarithmus wird mithilfe der Zehnerpotenz aufgelöst. Das folgende Beispiel zeigt die Berechnung der Spannungsverstärkung, wenn der Verstärker ein Eingangssignal entweder um 40 dB verstärkt oder mit −40 dB dämpft.
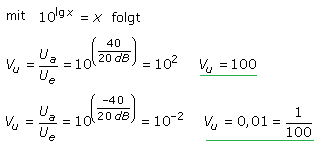
Pegel
Unter Pegel versteht man ein logarithmisches Verhältnis mit fest definierter Bezugsgröße gleicher Dimension. Pegel sind wie die relativen Verhältnismaße ebenfalls dimensionslos. Pegelwerte sind Absolutwerte, daher muss der Bezugswert mit angegeben werden. Vielfach wird die Pseudoeinheit dB mit einem weiteren Buchstaben oder dem beschreibenden Einheitenzeichen erweitert. Diese Schreibweise entspricht nicht der IEC-Norm und ist besonders im Fernmeldewesen bei der ITU üblich.
Die Übertragungstechnik der Akustik rechnet mit 1 mW als Bezugswert der Leistung an 600 Ω und nutzt damit den Standard des Fernmeldewesens. Für den Spannungspegel folgt daraus die Bezugsspannung von 775 mV. Die HF-Technik verwendet als Leistungsbezug ebenfalls 1 mW aber an 50 Ω. Für einen Spannungspegel errechnen sich damit 224 mV als Bezugsspannung. Die Fernsehtechnik bezieht sich auf 1 mW an 75 Ω, womit eine Bezugsspannung von 274 mV folgt. In der Antennentechnik ist 1 μV der definierte Spannungsbezug. Häufigere Bezugswerte können auch 1 W beim Leistungspegel und 1 V beim Spannungspegel sein. Feldstärkemessungen beziehen sich auf 1 W/m2 und 1 V/m. In der Akustik werden Schalldruckpegel auf den Bezugswert 20 μPa in Luft und 1 μPa in Wasser und anderen Medien für die Frequenz 1 kHz definiert. Der Wert wurde nicht an die menschliche Hörschwelle, die im Bereich von 3 kHz liegt, angepasst. Für jeden Bezugswert hat der Pegel den Wert 0 dB mit der entsprechenden Benennung, wie es die folgende Tabelle zeigt.
| Bezeichnung | Formelzeichen | Kurzzeichen | Bezugswert |
|---|---|---|---|
| Leistungspegel an 600 Ω | LP, nP, p | dB(m) | 1 mW |
| absoluter Spannungspegel | LU, nU, pu | dB(u) | 0,775 V |
| Spannungspegel | LU, nU | dB(V) | 1 V |
| Antennenpegel an 75 Ω | LU, nU | dB(μV) | 1 μV |
| Schalldruckpegel | Lp, SPL | dB(μPa) | 20 μPa |
Die Bezeichnungen können sehr freizügig gewählt werden. So wird für Pegel der Buchstabe L wie Level oder n wie Niveau ebenso wie p mit dem entsprechenden Index als Pegel für Spannung, Leistung usw. benutzt. Zur Veranschaulichung folgen einige Berechnungsbeispiele:

Für festgelegte Impedanzen können Spannungspegel in ihre Leistungspegel umgerechnet werden. Für die Antennentechnik ist 1 μV Bezugsspannung definiert. In der TV-Technik gilt Leistungsanpassung an 75 Ω Impedanz. Für diesen Anschlusswert kann der Spannungspegel 60 dB(μV) in den entsprechenden Leistungspegel umgerechnet werden.

Full-Scale-Pegelwert
Pegelangaben in dB(FS) gehören zur digitalen Audiotechnik. Ein Analog-Digital-Wandler gibt bei analoger Vollaussteuerung einen Digitalwert mit nur 1111... aus, den maximalen Skalenendwert, der dem Referenzwert für 0 dB(FS) entspricht. Alle anderen Werte sind kleiner und die dB(FS)-Pegelwerte daher negativ. Der niedrigste Wert des digitalen Wandlers eines analogen Eingangspegels zeigt nur 0000... Von der Auflösung der Quantisierung abhängig wird das Verhältnis zur Vollaussteuerung in dB angegeben und entspricht bei 8 Bit mit 255 Stufen −48 dB(FS), bei 16 Bit mit 65535 Stufen −96 dB(FS). Soll der Wandler positive und negative Spannungen verarbeiten, muss der Wertebereich halbiert und genaugenommen der Nullpunkt berücksichtigt werden.
Pegeldiagramm
Jedes Eingangssignal eines Zweipols verstärkt oder dämpft das Signal. Bilden die Zweipole in Serie geschaltet eine Übertragungskette (Kaskade), so wird das Ausgangssignal des vorangehenden Glieds als Eingangssignal der Folgestufe wieder verstärkt oder gedämpft. Die Gesamtverstärkung errechnet sich durch die Multiplikation der einzelnen Faktoren, wobei Verstärkungsfaktoren größer 1 und Dämpfungsfaktoren kleiner 1 sind. Die Rechnung vereinfacht sich mithilfe der Pegelwerte. Die Pegel werden addiert. Werden die logarithmischen Maße durchgehend mit dem Formelzeichen a bezeichnet, dann stehen positive Werte für Verstärkungen und negative Werte für Dämpfungen. Teilweise steht (stand) das Formelzeichen a für Dämpfung (attenuation) mit positivem Wert. Die Verstärkung V (v) oder G (g) hat stets positive Werte. Das Beispieldiagramm stellt eine angepasste Übertragungsstrecke dar.
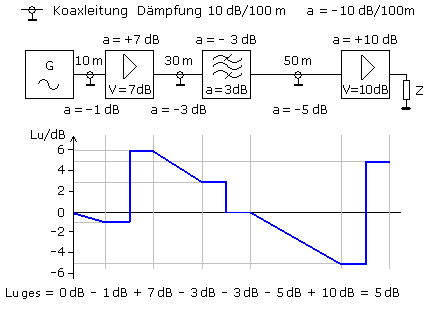
Addition von Leistungs- und Leistungswurzelwerte
Nur in einer Kaskadenschaltung können die Pegelwerte addiert werden. Zwei Verstärker, die ohne festen Phasenbezug (nicht korreliert) einen Raum beschallen, erzeugen nicht ihren Summenpegel. Die Einzelpegel müssen vor der Addition in die linearen Leistungswerte delogarithmiert werden. Die Summe kann anschließend in den dann richtigen Pegelwert logarithmiert werden. Entsprechendes gilt für unkorrelierte Spannungsquellen, die als Summenspannung ein neues Signal bilden.