Das Komplement in der Mathematik

In der Digitaltechnik werden Subtraktionen fast immer als Addition ausgeführt, wobei ein bestimmtes Komplement des zu subtrahierenden Werts addiert wird. Der Vorteil ist es mit nur einer Rechenschaltung zwischen einem positiven und negativen Ergebnis unterscheiden zu können. Viele alte mechanische Rechenmaschinen hatten nur Addierwerke und konnten mit der Eingabe des richtigen Komplementwerts auch subtrahieren. Der Begriff des Komplements in der Mathematik ist eng verbunden mit der Mengenlehre und Zahlen lassen sich ebenfalls Mengen zuordnen.

Menge der ganzen Zahlen

Alle positiven und negativen ganzen Zahlen einschließlich der Null bilden die Menge der ganzen Zahlen. Mit dieser Menge sind alle Additionen, Subtraktionen und Multiplikationen uneingeschränkt möglich. Mathematiker nutzen zur Beschreibung dieser Menge die beiden gleichberechtigten Darstellungen.

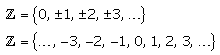
Menge der natürlichen und positiven ganzen Zahlen

Philosophisch betrachtet ist die Natur nur positiv eingestellt. Alles Negative hat auf Dauer keinen Bestand und verschwindet. Der zeitliche Ablauf geht nur in die positive Richtung und nicht zurück ins Negative.

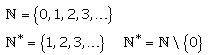
Die Menge der natürlichen Zahlen umfasst alle positiven ganzen Zahlen einschließlich der Null. Sie ist nach DIN 5473 Element dieser Menge und auch in der Digitaltechnik ist die dezimale 0 als positiver Wert definiert. Definiert ist noch die Menge der positiven ganzen Zahlen, in der die Null nicht vorkommt. Das kann auch mit den Symbolen der Mengenlehre beschrieben werden. Mit beiden Mengen sind Additionen und Multiplikationen uneingeschränkt möglich.

Komplement – Komplementmenge

Das Komplement einer Menge A, geschrieben als A^C, ist definiert als die Menge aller Elemente x, die nicht Element der Menge A sind. Nimmt man zum Beispiel die Menge der positiven ganzen Zahlen und unterteilt sie in die Teilmenge der geraden ganzen Zahlen und in die Teilmenge der ungeraden ganzen Zahlen, dann stellen beide Teilmengen zueinander das Komplement dar.

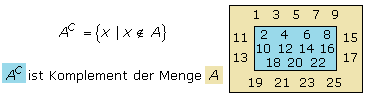
Gelesen wird die Definitionszeile als: Das Komplement von A ist die Menge aller Elemente x für die gilt, dass x kein Element von A ist. In der Skizze enthält die Menge A ungerade ganze Zahlen. Das Komplement zu A oder A^C hat mit den geraden ganzen Zahlen nur Elemente, die nicht in A enthalten sind. Würde man die Menge der geraden ganzen Zahlen mit B bezeichnen, dann enthält das Komplement von B oder B^C nur ungerade ganze Zahlen, stellt somit die Menge A dar.

Das Komplement bezogen auf eine Grundmenge

Die geraden und ungeraden ganzen Zahlen bilden die Menge der positiven ganzen Zahlen. Diese Menge stellt im Folgenden die Grundmenge G oder übergeordnete Menge dar. Die Menge der geraden ganzen Zahlen (gZ) und die Menge der ungeraden ganzen Zahlen (uZ) sind Teilmengen dieser Grundmenge. Das Komplement C zu den ungeraden ganzen Zahlen C(uZ) bezogen auf die Grundmenge G hat alle Elemente x die zur Grundmenge gehören und x kein Element der ungeraden ganzen Zahlen ist. Das Komplement C(uZ) enthält als Elemente nur gerade ganze Zahlen.

Differenzmenge

Betrachtet man das letzte Beispiel und zieht aus der Grundmenge alle ungeraden ganzen Zahlen heraus, bleibt als Rest- oder Differenzmenge die der geraden ganzen Zahlen. Die Differenzmenge ist durch die folgende Gleichung definiert:

Die Definitionsgleichung besagt: Die Differenzmenge der Mengen A und B ist die Menge aller Elemente, die zu A, nicht aber zu B gehören. Vergleicht man die Definitionsgleichungen der Differenzmenge mit dem auf eine Grundmenge bezogenen Komplement einer Teilmenge, so sind beide identisch. Voraussetzung ist, die Menge, zu der die Komplementmenge gebildet wird, ist Teilmenge der Grundmenge. Es besteht ein Zusammenhang zwischen dem Komplement und der Subtraktion.

Das Komplement im Zahlensystem

Ein Komplement kann als das Umgekehrte zu einer Basis angesehen werden. Die Basis im Dezimalsystem ist die 10. Eine Dezimalzahl zwischen 0 und 9 und ihr Zehnerkomplement addiert sich somit zur Basis 10. Verallgemeinert gesagt ergänzen sich eine Dezimalzahl und ihr Zehnerkomplement zum nächsten Zehnerexponenten. Im Dualsystem mit der Basis 2 wird eine Binärzahl durch ihr Zweierkomplement zum nächsten Zweierexponenten ergänzt. Mit dem Komplement kann eine Subtraktion als Addition ausgeführt werden.

Neunerkomplement

Die folgenden Betrachtungen beziehen sich auf das Dezimalsystem. Ein mechanischer Umdrehungszähler hat auf jeder Scheibe die Ziffern 0 ... 9. Normalerweise gibt es nur eine Drehrichtung und mit jeder Umdrehung wird zur Anzeige 1 addiert. Nach der vollständigen Umdrehung einer Scheibe steht sie wieder auf 0 und ein Mitnehmernocken dreht die Nachbarscheibe der Zehnerstelle auf 1. Es handelt sich um ein Addierwerk.

Ein Umkehren der Drehrichtung entspricht der Subtraktion. Die Anzeige ist nur dann korrekt, solange der abzuziehende Wert kleiner oder gleich dem angezeigten Wert ist. Mit nur einer Drehrichtung ist eine direkte Subtraktion nicht möglich. Steht zum Beispiel die Anzeige auf 3 und es soll 2 subtrahiert werden, muss am Ende 1 angezeigt werden. Dreht man das Rad um 7 Stellungen vor, dann steht seine Anzeige auf 0 und die Zehnerstelle auf 1. Dieser Übertrag wird zur Einerstelle addiert, die dann das zu erwartende Ergebnis anzeigt.

Anstelle der Subtraktion wird das Neunerkomplement (Stellenkomplement) der zu subtrahierenden Zahl addiert und der Stellenübertrag zum Ergebnis addiert. Der im Anzeigewerk stehende Übertrag wird danach nicht mehr beachtet. Das Neunerkomplement entsteht durch Subtraktion einer Zahl von 9 und ist damit der Ergänzungswert der Zahl zu 9. Beim Rechnen mit Komplementwerten muss auf gleiche Stellenzahl geachtet werden. Das Neunerkomplement mehrstelliger Zahlen entsteht aus den Neunerkomplementen jeder einzelnen Stelle.

Ist der Subtrahend größer als der Minuend, so ergibt sich ein negatives Ergebnis. Das Addierwerk kann mithilfe des Neunerkomplements auch diese Aufgaben berechnen. Bei der Addition des Neunerkomplements entsteht kein Übertrag. Das charakterisiert ein negatives Ergebnis. In der Anzeige steht jetzt das Neunerkomplement vom eigentlichen Endergebnis, daher muss nochmals das Neunerkomplement gebildet werden.

Zehnerkomplement

Im Dezimalsystem ist das Zehnerkomplement die Ergänzungszahl oder Differenz zur nächsten Zehnerpotenz. Folglich ist das Zehnerkomplement einer dreistelligen Dezimalzahl ihr Ergänzungswert zu 1000. Man erhält es auch beim Addieren von 1 zum Neunerkomplement. Soll eine Dezimalzahl stellenweise in ihr Zehnerkomplement gewandelt werden, ist die Einerstelle zu 10 und alle anderen Stellen sind auf 9 zu ergänzen.

In vielen mechanischen Rechenwerken wird die Subtraktion als Addition des Zehnerkomplements ausgeführt. Hat der Subtrahend wie im zweiten Beispiel weniger Stellen als der Minuend, so ist er vor dem Bilden des Zehnerkomplements mit führenden Nullen auf die gleiche Stellenzahl zu bringen. Vor der Ergebnisanzeige musste noch 1 addiert werden. Die Rechenwerke hatten zur Eingabe des Subtrahenden auf der Tastatur die Ergänzungsziffern zu 9 etwas kleiner mit angegeben. Das Rechenwerk zeigt das Endergebnis an, wobei entweder die 1 in der höchsten Stelle nicht mehr angezeigt werden kann oder nicht beachtet wird.

Ist der Subtrahend größer als der Minuend, dann ist das Ergebnis negativ. Wird die Subtraktion durch die Addition mit dem Zehnerkomplement ersetzt, gibt es keinen Übertrag. Das charakterisiert ein negatives Ergebnis. Das Rechenwerk zeigt als Zwischenergebnis das Zehnerkomplement an. Das Endergebnis ist dann der negative Wert des Zehnerkomplements.

Soll eine größere Dezimalzahl von einer kleineren subtrahiert werden, so weiß man, das Ergebnis ist negativ. Man kann daher ebenso gut die kleinere Zahl von der größeren Zahl subtrahieren und vor das dann positive Ergebnis das Minuszeichen setzen.

45 − 68 = −23 mit Komplement: 99 − [45 + (99 − 68 + 1)] + 1 = 100 - [45 + (100 − 68)] = 68 + 45 = 23

Nichts anderes passiert in den Beispielen mit größerem Subtrahenden. Zum Minuenden wird das Stellenkomplement, das Neunerkomplement des Subtrahenden und der Wert 1 addiert. Es fehlt der Übertrag in die nächste Zehnerpotenz, also ist das Ergebnis negativ. Vom Zwischenergebnis ist daher das Stellenkomplement als Neunerkomplement zu bilden und 1 zu addiert. Das entspricht dem Zehnerkomplement, dessen negativer Wert das Endergebnis ergibt.

Zweierkomplement

Auch im Binärsystem kann die Subtraktion durch eine Addition ersetzt werden. Das ist von Nutzen, da für beide Rechenoperationen nur eine Rechnerschaltung benötigt wird. Im Binärsystem mit der Basiszahl 2 ist dazu das Zweierkomplement zu bilden. In Analogie zum oben beschriebenen Dezimalsystem gelangt man zum Zweierkomplement K2 durch die Addition von binär 1 zum Stellenkomplement, dem Einerkomplement K1 der Binärzahl. Die bitweise XOR Verknüpfung aller Bits einer Binärzahl führt zur invertierten Darstellung, dem Einerkomplement. Die Addition von binär 1 ergibt das Zweierkomplement: K1 + 1 = K2. Bei den Rechenoperationen mit Komplementen ist auf eine festgelegte Datenwortlänge zu achten. Nicht genutzte Bits werden mit 0 aufgefüllt. Im Einerkomplement steht eine 1 an diesen Stellen.

Das folgende Beispiel verwendet ein 4-Bit Datenwort. Zur Dezimalzahl 3 wird das binäre Einerkomplement bestimmt, indem von der Bitfolge 1111 stellenweise 0011 subtrahiert wird. Das Ergebnis 1100 steht im Zahlenkreis für dezimal −4. Das Zweierkomplement folgt durch Addition von 1 und entspricht für die Dezimalwerte mathematisch geschrieben der Gleichung Gl.(1) und allgemein für die Dezimalzahl a und einer beliebigen Stellenzahl n zur Basis 2 der Gleichung Gl.(2).

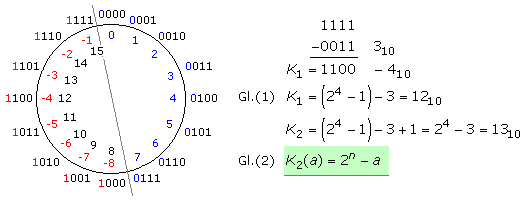
Der Nachweis, dass die Subtraktion zweier positiver ganzer Zahlen in eine Addition mithilfe des Komplements des Subtrahenden ersetzbar ist, zeigen die folgenden Gleichungen: