Logarithmusfunktionen

Mit der ab 1980 rasanten Weiterentwicklung der Elektronik und Digitalisierung ist das Lösen mathematischer Probleme bei hoher Genauigkeit sehr einfach geworden. Das schriftliche Rechnen mit sehr großen und/oder kleinen Zahlen war ohne diese Hilfsmittel zeitaufwändig und anfällig für kleine Flüchtigkeitsfehler. Mithilfe der Logarithmen vereinfachten sich die Multiplikationen und Divisionen auf Zwischenschritte mit Addition und Subtraktion. Das Potenzieren und Wurzelziehen für beliebige Exponenten wird mit Logarithmen zur Multiplikation und Division. Dazu gab es Logarithmentafeln mit vier- bis siebenstelligen Mantissen. Bis zum Abitur reichte das vierstellige Tafelwerk aus. Für höhere Genauigkeiten im naturwissenschaftlichen Bereich der Uni mussten es mindestens fünf- oder siebenstellige Logarithmentafeln sein. Das erste mechanische Hilfsmittel war der Rechenschieber. Er funktioniert für den Anwender nicht direkt erkennbar auf einem logarithmischen Prinzip. Sofern man mit Zehnerpotenzen umgehen konnte, erhielt man Ergebnisse mit einer Genauigkeit von zwei Stellen nach dem Komma viel schneller als mithilfe von Logarithmentafeln.

Der Taschenrechner erleichtert das Rechnen mit Logarithmen und liefert unverzögert Ergebnisse sehr hoher Genauigkeit. Alle Rechner verfügen über eine LG- oder LOG- und LN-Taste für die beiden bekanntesten Logarithmen. Im praktischen Leben treffen wir eher unbemerkt oft auf Logarithmen. Die Schallausbreitung in den verschiedenen Medien wird mit einer logarithmischen Schalldruckformel beschrieben. Das menschliche Ohr nimmt Tonhöhen- und Lautstärkeunterschiede in logarithmischer Abhängigkeit wahr. Erwärmung und Abkühlung physikalischer und chemischer Prozesse erfolgen mit exponentieller Gesetzmäßigkeit. Biologische Wachstums- und Stoffwechselprozesse verlaufen exponentiell. Der radioaktive Zerfall, die Auf- und Entladung kapazitiver elektrischer Speicher, der Elektromagnetismus, chemische Stoffumwandlungen und pH-Wertänderungen, alles erfolgt mit exponentieller Gesetzmäßigkeit. Zins-, Zinseszins- und Kreditformeln gehören dazu. Die Berechnungen der Stoffmengen, Reaktions- und Regelzeiten oder anderer exponentieller Parameter erfolgen daraus mithilfe der Logarithmen. Im IT-Bereich werden Informationen durch die Zahl der Zustände, der Bits ebenfalls logarithmisch berechnet.

Allgemeine Logarithmusfunktion

Die folgende Grafik zeigt Logarithmusfunktionen als Umkehrfunktionen zu ihren Exponentialfunktionen. In logarithmischen Funktionsgleichungen steht die Variable als log(x). In der Exponentialfunktion steht die Variable als Exponent einer Basiszahl a·exp(x). Der Funktionswert g(x) errechnet sich, für ganze Zahlen einfach zu erkennen, indem die Basis x-mal mit sich selbst multipliziert wird. Die Basis wird mit dem Exponenten potenziert. Da die Exponentialfunktionen einen streng monotonen Verlauf haben, können die Logarithmenfunktionen als ihre Umkehrfunktionen hergeleitet werden. Mit ihnen kann für jeden Funktionswert g(x) der Exponent (x) berechnet werden, mit dem die Basis (a) potenziert wurde. Um beide Funktionsarten im selben Achsenkreuz darzustellen, werden in der Umkehr- oder Logarithmusfunktion x und y getauscht. Die Grafik zeigt den Kurvenverlauf der meist verwendeten Logarithmusfunktionen für die Basis a = 10 (rot), a = e = 2,71828... (blau) und a = 2 (grün).

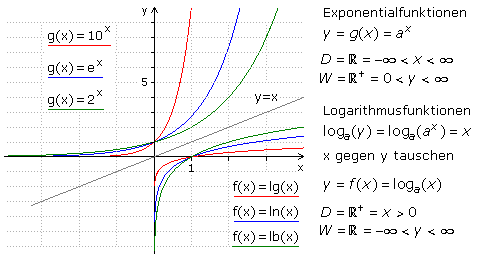
Für den Zehner-, Dekadischen oder Briggschen Logarithmus wird das Symbol lg verwendet. Der natürliche Logarithmus mit der Eulerschen Zahl e als Basis ist durch das Symbol ln (logarithmus naturalis) gekennzeichnet. Für den binären Logarithmus mit der Basiszahl 2 ist das Symbol lb (logarithmus binär) oder ld (logarithmus dual) üblich. Für jede andere Basis wird log mit der Basiszahl als Index geschrieben. Abweichend davon ist die Logarithmusfunktion log(x) in den IT-Programmiersprachen auf die Basis e bezogen und somit mathematisch gleich ln(x). Basiszahlen können alle positiven reellen Zahlen größer null und ungleich 1 sein. Der Graph der Logarithmusfunktion mit a > 1 ist streng monoton wachsend und mit 0 < a < 1 streng monoton fallend.

Alle Logarithmusfunktionen haben bei x = 1 ihre Nullstelle und nähern sich für x = 0 asymptotisch der y-Achse. Es ist zu erkennen, dass weder der Logarithmus von null noch von negativen Zahlen definiert ist. Der Logarithmus der Basis 1 ist nicht sinnvoll und wird von der Definition ausgeschlossen, da jede Potenz der Basis 1 als Ergebnis 1 liefert. Das Ergebnis beim Logarithmieren eines Werts, er wird als Numerus bezeichnet, ist der Exponent, mit dem die Basis potenziert werden muss, um diesen Numerus zu erhalten.

Der Logarithmus einer negativen Zahl ist nicht definiert, da ihre Umkehrfunktion, die Exponentialfunktion nur für positive reelle Zahlen definiert ist. Alle Elemente der Bildmenge, dem Wertebereich einer Exponentialfunktion liegen zwischen 0 < y < ∞. Diese Bildmenge wird für die Logarithmusfunktion zur Definitionsmenge und schließt somit negative Werte aus.

Logarithmengesetze

Am einfachsten kann man sie sich für den Zehnerlogarithmus herleiten, wenn man die Exponentialgesetze kennt. Da der Graph aller Logarithmusfunktionen von ihrer Basis unabhängig qualitativ den gleichen Verlauf hat, gelten die Logarithmengesetze uneingeschränkt für alle Logarithmen. Mit dem Logarithmus einer Zahl wird der Exponent ermittelt, mit dem die Basis des Logarithmus zu potenzieren ist, um die Zahl zu erhalten.

Logarithmus eines Produkts

Es soll der Logarithmus von 100000 = 100·1000 bestimmt werden. Das Ergebnis muss 5 sein. Der Logarithmus von 100 ergibt den Exponenten 2 und von 1000 den Exponenten 3. Der Logarithmus eines Produkts ist gleich der Summe der Logarithmen der einzelnen Faktoren.

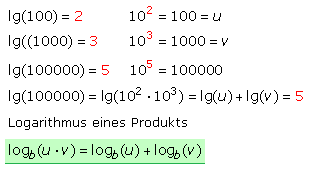
Logarithmus eines Quotienten

Es soll der Logarithmus von 100 = 10000 / 100 bestimmt werden. Das Ergebnis muss 2 sein. Der Logarithmus eines Quotienten ist gleich der Differenz aus den Logarithmen des Zählers und Nenners.

Logarithmus eines Exponentialausdrucks

Der Wert 1000 exponentiell geschrieben ist 10³. Wird der Logarithmus lg(10³) als Produkt lg(10·10·10) geschrieben, folgt nach der hergeleiteten Produktregel das Ergebnis 3. Der Logarithmus seiner eigenen Basis hat immer das Ergebnis 1, da der Exponent errechnet wird, mit dem die Basis zu potenzieren ist. Ist dieser Wert aber die Basis, so muss der Exponent den Wert 1 haben. Ein Wert mit negativem Exponenten ist gleich seinem Kehrwert mit positivem Exponenten.

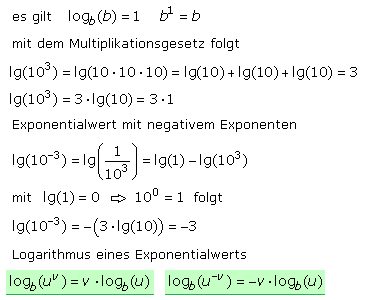
Logarithmus eines Wurzelausdrucks

Hierfür muss keine eigenständige Rechenregel aufgestellt werden, da der Wurzelexponent für den Wert (Radikand), aus dem die Wurzel zu ziehen ist, als gebrochener Exponent erscheint. Es gilt also die Rechenregel für den Logarithmus aus Exponentialausdrücken. Der Exponent wird zum Faktor, der mit dem Logarithmus des Radikanden multipliziert wird. Die dritte Wurzel aus 1000 ist 10 und wie weiter oben beschrieben, gilt lg(10) = 1. Der Logarithmus der dritten Wurzel aus 1000 sollte daher 1 sein.

Logarithmus von der Potenz einer Potenz

Auch hierfür kann die Rechenregel für den Logarithmus eines Exponentialausdrucks angewendet werden. Die Potenz einer Potenz wird zuvor als neue Potenz, dem Produkt der beiden Exponenten geschrieben.

Umrechnen von Logarithmen unterschiedlicher Basis

In einer Exponentialfunktion steht die Variable im Exponenten und wird durch Logarithmieren zum Faktor. In den meisten Fällen wird die Basis irgendeine Zahl sein, sodass ein normales Rechenprogramm mit dem Dekadischen-, oder Natürlichen Logarithmus nicht weiter hilft. Es gibt eine einfache Möglichkeit zur Umrechnung der Basen. Das folgende, auch ohne Hilfsmittel lösbare Beispiel funktioniert mit dem Logarithmus zur Basis 3. Es zeigt am Ende die allgemeine Rechenregel für Logarithmen unterschiedlicher Basen.

Einfach-logarithmisches Achsensystem

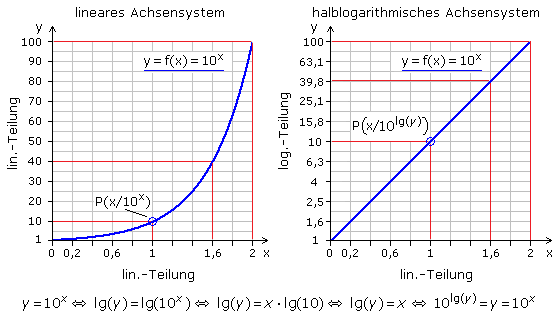
Ist im zweidimensionalen Achsenkreuz eine Achse linear und die andere logarithmisch geteilt, handelt es sich um ein einfach-, oder halb-logarithmisches Achsensystem. In der Mathematik hat fast immer die x-Achse der Variablen eine lineare und die y-Achse der Funktionswerte eine logarithmische Teilung. Bei der Darstellung einer Exponentialfunktion im linear geteilten Achsensystem sind Punktkoordinaten nur ungenau ablesbar. Die Funktionswerte für x > 1 nehmen in kleinen Intervallen sehr schnell zu, während bei gleichem Maßstab im Bereich bis x = 1 die Änderungen sehr gering sind. Mit einer halblogarithmischen Teilung wird der Funktionsgraph zur Geraden und die Änderungen sind optimal ablesbar.

Doppelt-logarithmisches Achsensystem

Einfache Potenz- oder Polynomfunktionen nehmen sehr schnell innerhalb kleiner Variablenintervalle große Werteintervalle an. Zur Darstellung der Funktionsgraphen ist es besser, für beide Achsen die logarithmische Teilung zu wählen. Der Funktionsgraph ist dann eine Gerade und die Geradensteigung entspricht dem Wert des Exponenten.

Die Eigenschaften von Verstärker- und/oder Signalübertragungsketten werden oft in Abhängigkeit eines Frequenzbandes dargestellt. Der Audio-Frequenzbereich reicht von 0 bis 20 kHz, sodass nur die logarithmische Achseneinteilung sinnvoll ist. Das Leistungs- oder Spannungsverhältnis wird in logarithmischen Dezibel Werten angegeben. Für eine Signalstrecke vereinfachen sich die Berechnungen für Verstärkungen und Dämpfungen mit dB-Werten. Diese logarithmischen Werte sind meist ein bis zweistellige Ganzzahlen. Sie werden einfach addiert oder subtrahiert. Als nicht logarithmische vielstellige Werte müssten sie sonst multipliziert oder dividiert werden.

Logarithmengleichungen

Die zu bestimmende Variable kann im Logarithmanden, dem zu logarithmierenden Term stehen. Beide Seiten der Gleichung werden zur Exponentialfunktion mit der Basis des Logarithmus geschrieben und damit für die Variable linearisiert. Steht die Variable im Exponenten des zu logarithmierenden Terms, so kann der Exponent als Faktor vor den Logarithmus der Basis des Exponenten geschrieben werden. Im Anschluss daran wird die Gleichung nach der Variablen umgestellt. Ist die Variable die Basis des Logarithmus, wird die Gleichung in eine Exponentialgleichung der Variablen umgewandelt, um den Logarithmus aufzuheben.

Erste Ableitung der elementaren Logarithmusfunktionen

Es ist zwischen dem natürlichen Logarithmus und dem zu einer beliebigen Basis zu unterscheiden. In jeder mathematischen Formelsammlung stehen die beiden 1. Ableitungen. Exponentialfunktionen und Logarithmusfunktionen sind Umkehrfunktionen. Die Ableitung von y = f(x) = ln(x) kann schnell und einfach hergeleitet werden. Wie weiter oben in diesem Artikel gezeigt, kann der Logarithmus einer beliebigen Basis einer Zahl mithilfe der zur Verfügung stehenden Logarithmenfunktionen berechnet werden. Wird er durch den natürlichen Logarithmus ersetzt, dann ist die Herleitung der 1. Ableitung kein Problem, denn sie muss nur mit dem Kehrwert des natürlichen Logarithmus der anfänglichen Basis multipliziert werden.

Ist die Grenzwertbetrachtung zur Herleitung der Eulerschen Zahl e bekannt, kann die Ableitung mithilfe der Grenzwertbildung beim Differenzenquotienten auch etwas ausführlicher erfolgen. Die 1. Ableitung entspricht der Tangentensteigung in einem Punkt. Sie folgt aus dem Steigungsdreieck, wo durch die Grenzwertbildung die kleine Änderung (h) der x-Koordinate gegen null geht und so die Sekante zur Tangente wird.