Zahlenfolgen mit besonderen Eigenschaften

Es gibt nicht genug kleine Zahlen, um alle Anforderungen zu erfüllen, die an sie gestellt werden. (Richard K. Guy)

Daraus folgt – manchmal –, dass zufällig Dinge übereinstimmen, aus denen dann falsche Schlüsse gezogen werden können. Betrachtet man die alternierenden Summen von Fakultäten:

2! − 1! = 1
3! − 2! + 1! = 5
4! − 3! + 2! − 1! = 19
5! − 4! + 3! − 2! + 1! = 101
6! − 5! + 4! − 3! + 2! − 1! = 619
7! − 6! + 5! − 4! + 3! − 2! + 1! = 4421

Die Summe ist immer eine Primzahl. Die Frage ist nun, ob das so weiter geht     

Leonhard Euler (1703 - 1783), ein Schweizer Mathematiker erkannte, dass die Beziehung:
n² + n + 41 für ganzzahlige n immer Primzahlen liefert. Diese Aussage stimmt leider nur bis n = 40.

Noch ein überraschendes Beispiel. Durch Ausmultiplizieren erhält man:

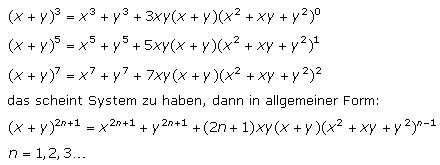
...oder vielleicht auch nicht     

Der ziemlich kompliziert aussehende Bruch liefert für alle positiven ganzzahligen n immer das gleiche Ergebnis.
Der Ausdruck n!, gelesen als n Fakultät, bedeutet dabei: 1·2·3·...·n , somit ist 4! = 24

Die beiden nächsten Zahlenfolgen sind mathematisch nicht lösbar. Sie stammen aus der Serie Spaß mit Zahlen von Prof. Albrecht Beutelspacher, aus der Zeitschrift: Bild der Wissenschaft.

Hier die erste Gemeinheit: Gesucht ist das nächste Glied der Zahlenfolge:

8,  3,  1,  5,  9,  6,  7,  4,  ...    

Hier eine weitere geheimnisvolle Folge – wohl noch etwas gemeiner:

1,  11,  21,  1211,  111221,  312211,  ...