Zyklische Zahlen

Die natürlichen Zahlen bilden die Menge aller positiven ganzen Zahlen. Darin gibt es nun Zahlen, die wegen ihrer besonderen Eigenschaft als zyklische Zahlen bezeichnet werden. Wird diese Zahl mit einer natürlichen Zahl von 1 bis n multipliziert, so weist das Produkt in derselben zyklischen Abfolge die gleichen Ziffern wie die Ausgangszahl auf.

Die kleinste zyklische Zahl ist die 1, wobei auch n = 1 ist. Ein trivialer Fall. Gesucht haben andere, und so schrieb Leonard Eugene Dickson in History of the Theory of Numbers, Washington 1932, dass all diese Zahlen Perioden von periodischen Zahlen sind. Man erhält sie aus dem Kehrwert einiger Primzahlen wie beispielsweise 7, 17, 19, 23, 29, 47, 59, 61, 97.

Schon zuvor entdeckte Lewis Carroll (1832 - 1898) ein Mathematiker und Schriftsteller in Oxford, im Kehrwert der Zahl 7 in der zyklischen Reihenfolge nach dem Komma die magische Zahl 142857. Carroll ist vielleicht bekannter unter dem Namen Charles Lutwidge Dodgson, dem Autor von Alice im Wunderland.

Zyklische oder magische Zahlen finden sich in periodischen Dezimalbrüchen, deren Periode eine konstante Länge aufweist, die genau um eine Stelle kleiner ist wie die Zahl selbst. Untersuchen wir daraufhin die Zahl 7 näher:

Der Kehrwert von 7 ergibt den periodischen Dezimalbruch: 1/7 = 0,142857142857142857...
Die Periode mit der Länge n = 6 ist die zyklische Zahl:  142857
Multipliziert man diese zyklische Zahl mit n = 1 ... 6 so ist die Ziffernfolge im Ergebnis eine zyklische Permutation der Zahl.

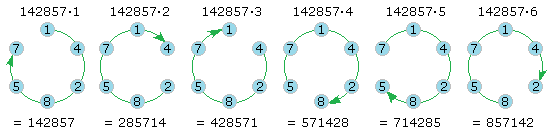
Es gibt noch einige Besonderheiten zu erwähnen: Die Summe der sich gegenüberstehenden Ziffern ist immer 9.
Multipliziert man die zyklische Zahl mit der Zahl, aus der sie gebildet wurde, so ist das Ergebnis eine Neunerreihe mit so vielen Stellen, wie die Periode selber lang ist: 142857 · 7 = 999999

Selbst der Kehrwert der zyklischen Zahl ist ein interessanter periodischer Dezimalbruch. Die Periode ist sechsstellig und die letzte Ziffer ist die ursprüngliche Primzahl: 1 / 142857 = 0,000007000007...

Ist das ein Zufall oder liegt ein System vor. Es soll noch mit der nächsten Primzahl, der 17 überprüft werden, die eine zyklische Zahl liefert. Wie zu sehen ist, stimmen die oben gemachten Aussagen auch hier.

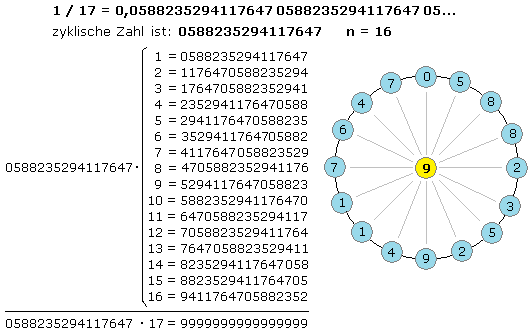
Der Kehrwert ist ebenfalls einen periodischen Dezimalbruch. Die Periode hat 16 Stellen und die ursprüngliche Primzahl am Ende:
1 / 0588235294117647 = 0,00000000000000170000000000000017....