RC-Phasenschieberbrücke als Allpassfilter

Mit Thyristoren und anderen triggerbaren Halbleiterbaugruppen kann im Wechselstromkreis mithilfe des Phasenanschnitts die elektrische Leistung ohne nennenswerte Leistungsverluste gesteuert werden. Der Laststrom wird nur bei bestimmten Phasenwinkeln der Wechselspannung eingeschaltet. Ohne den Einsatz spezieller Steuergeneratoren kann die Steuerspannung direkt aus der Versorgungsspannung gewonnen werden. Ein einfaches RC-Glied erzeugt die Phasenverschiebung, da die Spannung am Kondensator der Versorgungsspannung nacheilt. Mit einem Stellwiderstand im RC-Glied kann so der Phasenwinkel und damit der Zündzeitpunkt innerhalb eines größeren Bereichs eingestellt werden. Der Nachteil beim einfachen RC-Glied ist eine nicht konstante Amplitude der Steuerspannung.

Optimaleres Verhalten bietet ein RC-Phasenschieber in Brückenschaltung. Er besteht aus einem Widerstandsteiler mit parallel geschaltetem RC-Glied oder zwei gleich dimensionierte gegeneinander versetzt parallel liegende RC-Glieder. Die Schaltung kann als Phasenschieber oder einem später beschriebenen Allpassfilter verwendet werden. Als Ausgangsspannung wird die Brückenspannung genutzt, die für alle Phasenwinkel eine konstante Amplitude hat. Das Bild zeigt eine RC-Phasenschieberbrücke und das Diagramm den Kurvenverlauf für unterschiedlich eingestellte Phasenwinkel. Da Ausgangs- und Eingangsspannung keine gemeinsame Masse haben, erfolgte die Darstellung der Signale in Bezug zur Messmasse.

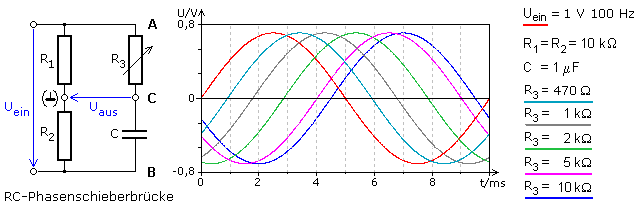
Für eine RC-Phasenschieberbrücke kann ein Zeigerdiagramm erstellt werden. Der linke Brückenzweig teilt mit R1 = R2 die Eingangsspannung symmetrisch auf. Zwischen den beiden Teilspannungen gibt es keine Phasenverschiebung. Im rechten Brückenzweig haben die Teilspannungen am Widerstand und Kondensator immer eine Phasenverschiebung von φ = 90°. Die Summenspannung über der RC-Schaltung ist gleich der Eingangsspannung.

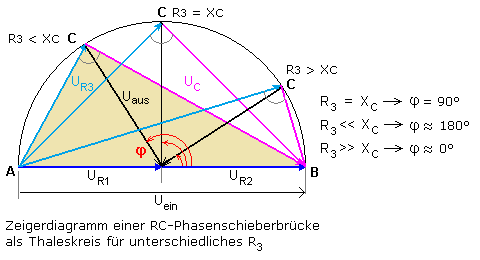
Wird in der Phasenschieberbrücke nur R3 verstellt, dann ändern sich die Teilspannungen für den rechten RC-Zweig aber die Spannungssumme bleibt mit Uein konstant. Der Punkt C wandert dabei auf einem Halbkreis mit dem Durchmesser AB. Nach dem bekannten Satz des Thales hat jedes Innendreieck mit der Hypotenuse AB, dem Halbkreisdurchmesser, dessen Katheten auf dem Halbkreis im Punkt C enden dort immer im rechten Winkel.

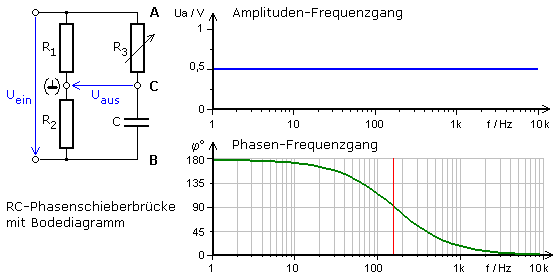
Im Punkt C ist es der Phasenwinkel zwischen UR3 und UC mit stets φ = 90°. Die Ausgangsspannung ist die Brückenspannung zwischen C und dem Massesymbol. Der schwarze Halbkreisradius stellt die Amplitude der Ausgangsspannung dar und ist für alle Einstellungen der Phasenschieberbrücke konstant und halb so groß wie die Eingangsspannung. Der Phasenwinkel zwischen der Ausgangsspannung und UR2 variiert zwischen 0° und 180°. Für die RC-Phasenschieberbrücke wurde mittels Simulationsprogramm ein Bodediagramm erstellt. Es zeigt für den Brückenzweig die halbe Eingangsspannung und den variablen Phasenwinkel zwischen 0° und 180°.

Allpassfilter

Im Gegensatz zur einfachen RC-Schaltung als Hoch- oder Tiefpass zeigt die RC-Phasenschieberbrücke eine von der Frequenz unabhängige Ausgangsspannung. Alle Eingangssignale unterschiedlicher Frequenz passieren die Schaltung mit konstanter Ausgangsamplitude. Die Phasenschieberdrücke wird auch als Allpassfilter bezeichnet. Bezogen auf das Eingangssignal erfährt das Ausgangssignal nur eine frequenzabhängige Phasenverschiebung und kommt mit zeitlicher Verzögerung am Ausgang der Schaltung an. In der Nachrichtentechnik werden Allpassfilter zur Phasenentzerrung und Laufzeitverzögerung eingesetzt.

Übertragungsfunktion des Allpassfilters

Für dieses Filter kann die Übertragungsfunktion hergeleitet werden. Die Brückenspannung errechnet sich aus der Spannungsdifferenz von U1 am Kondensator und U2 am Widerstand R2. Der Pass hat zwei Stromzweige, die an der gleichen Eingangsspannung liegen. Mit dem jeweiligen Zweigstrom kann eine Gleichung für die beiden Teilspannungen aufgestellt werden.

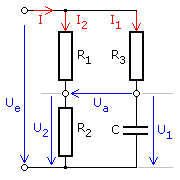
Für die dargestellte Phasenschieberbrücke gelten die folgenden Beziehungen: \[\underline I = {\underline I _1} + {\underline I _2}\quad \quad {\underline Z _1} = {R_3} + \frac{1}{{j\,\omega \,C}}\quad \quad {\underline Z _2} = {R_1} + {R_2}\] \[{\underline U _e} = {\underline I _1} \cdot {\underline Z _1}\quad \quad {\underline U _e} = {\underline I _2} \cdot {\underline Z _2}\] \[{\underline U _a} = {\underline U _1} - {\underline U _2}\quad \quad {\underline U _1} = {\underline I _1}\frac{1}{{j\,\omega \,C}}\quad \quad {\underline U _2} = {\underline I _2} \cdot {R_2}\] Für die Ausgangsspannung folgt durch geeignete Kombinationen und Umformungen: \[{\underline U _a} = {\underline U _e}\left( {\frac{{\frac{1}{{j\,\omega \,C}}}}{{{R_3} + \frac{1}{{j\,\omega \,C}}}} - \frac{{{R_2}}}{{{R_1} + {R_2}}}} \right)\quad \] Die Übertragungsfunktion ist das Verhältnis der Ausgangs- zur Eingangsgröße. Die erste Komponente im Klammerausdruck wird auf einen Hauptnenner gebracht, ausgerechnet und danach konjugiert komplex erweitert: \[\frac{{{{\underline U }_a}}}{{{{\underline U }_e}}} = \frac{1}{{1 + j\,\omega \,{R_3}\,C}} - \frac{{{R_2}}}{{{R_1} + {R_2}}} = \frac{{1 - j\,\omega \,{R_3}\,C}}{{1 + {{(\omega \,{R_3}\,C)}^2}}} - \frac{{{R_2}}}{{{R_1} + {R_2}}}\] Mit dem Erweitern auf einen Hauptnenner, dem Ausrechnen der Klammerausdrücke im Zähler und einem erneuten Ausklammern folgt: \[\frac{{{{\underline U }_a}}}{{{{\underline U }_e}}} = \frac{{{R_1} - {R_2} \cdot {{(\omega \,{R_3}\,C)}^2} - j\,\omega \,{R_3}\,C \cdot ({R_1} + {R_2})}}{{({R_1} + {R_2}) \cdot \left( {1 + {{(\omega \,{R_3}\,C)}^2}} \right)}}\] Die Übertragungsfunktion mit getrennt geschriebenen Real- und Imaginärkomponenten ergibt sich zu: \[\frac{{{{\underline U }_a}}}{{{{\underline U }_e}}} = \frac{{{R_1} - {R_2} \cdot {{(\omega \,{R_3}\,C)}^2}}}{{({R_1} + {R_2}) \cdot \left( {1 + {{(\omega \,{R_3}\,C)}^2}} \right)}} - \left( {\frac{{\omega \,{R_3}\,C}}{{1 + {{(\omega \,{R_3}\,C)}^2}}}} \right) \cdot j\]

Amplitudengang des Allpassfilters

Sehr wahrscheinlich gilt für die Widerstände R1 = R2 und können durch R ersetzt werden. Zur weiteren Übersichtlichkeit wird die Zeitkonstante τ = R3·C eingeführt. Mit wenigen Umformungen und der Erweiterung zum Hauptnenner hat die Übertragungsfunktion die Form: \[\frac{{{{\underline U }_a}}}{{{{\underline U }_e}}} = \frac{{1 - {{(\omega \,\tau )}^2}}}{{2\,\left[ {1 + {{(\omega \,\tau )}^2}} \right]}} - \left( {\frac{{2\,\omega \,\tau }}{{2\,\left[ {1 + {{(\omega \,\tau )}^2}} \right]}}} \right) \cdot j\] Der Amplitudengang errechnet sich aus der Wurzel der Summe der Komponentenquadrate. Der Hauptnenner bleibt als Faktor bestehen: \[\left| {\frac{{{{\underline U }_a}}}{{{{\underline U }_e}}}} \right| = \frac{{\sqrt {{{\left[ {1 - {{(\omega \,\tau )}^2}} \right]}^2} + 4\,{{(\omega \,\tau )}^2}} }}{{2\,\left[ {1 + {{(\omega \,\tau )}^2}} \right]}}\] Wird im Zähler der Radikand ausgerechnet, so vereinfacht so das Ergebnis zu: \[\left| {\frac{{{{\underline U }_a}}}{{{{\underline U }_e}}}} \right| = \frac{{\sqrt {1 + 2\,{{(\omega \,\tau )}^2} + {{(\omega \,\tau )}^4}} }}{{2\,\left[ {1 + {{(\omega \,\tau )}^2}} \right]}} = \frac{{\sqrt {{{\left[ {1 + {{(\omega \,\tau )}^2}} \right]}^2}} }}{{2\,\left[ {1 + {{(\omega \,\tau )}^2}} \right]}} = \frac{1}{2}\] Das Ergebnis entspricht dem des Amplituden-Frequenzgangs im Bodediagramm im ersten Seitenabschnitt. Hat das Allpassfilter gleiche Werten im ohmschen Widerstandsteiler, dann ist die Amplitude des Ausgangssignals halb so groß wie die Eingangsamplitude.

Phasengang des Allpassfilters

Auf das Eingangssignal bezogen errechnet sich die frequenzabhängige Phasenlage des Ausgangssignals mithilfe des Arcustangens aus dem Quotienten der Imaginär- zur Realkomponente. \[\varphi (\omega ) = \arctan \left( {\frac{{ - 2\,\omega \,\tau }}{{1 - {{(\omega \,\tau )}^2}}}} \right) = \arctan \left( {\frac{{2\,\omega \,\tau }}{{{{(\omega \,\tau )}^2} - 1}}} \right)\] \[\begin{array}{l} \omega \to 0\quad \arctan ( \to - 0)\quad \varphi \to 180^\circ \\ \omega \to \infty \quad \arctan ( \to + 0)\quad \varphi \to 0^\circ \end{array}\] Für den Phasenwinkel φ = 90° strebt der Klammerausdruck gegen unendlich und sein Kehrwert gegen null. Als Gleichung betrachtet folgt dann: \[\frac{{{{(\omega \,\tau )}^2} - 1}}{{2\,\omega \,\tau }} \to 0\quad \Rightarrow {({\omega _g}\,\tau )^2} - 1 = 0\quad \Rightarrow {\omega _g}\,\tau = 1\] \[{f_g} = \frac{1}{{2\,\pi \,{\omega _g}}} = \frac{1}{{2\,\pi \,{R_3}\,C}}\] Im oben gezeigten Zeigerdiagramm (Thaleskreis) ist bei gleichen Widerstandswerten von R3 und XC der Phasenwinkel φ = 90°. Bei einem RC-Pass ist bei der Grenzfrequenz das Widerstandsverhältnis gleich und der Phasenwinkel beträgt 45°. Die Grenzfrequenzen sind nicht vergleichbar.

Aus dem weiter oben gezeigten Zeigerdiagramm (Thaleskreis) ist zu erkennen, dass bei gleichen Widerstandswerten von beträgt. Dieser Fall ist bei der Grenzfrequenz des RC-Glieds gegeben, die aber nicht die Grenzfrequenz des Allpasses ist.

Aktives Allpassfilter 1.Ordnung

Bei der RC-Phasenschieberbrücke fehlt der Massebezug zwischen Ausgangs- und Eingangssignal. Im aktiven Allpassfilter mit einem Operationsverstärker (OPV) hat das Eingangs- als auch Ausgangssignal den gleichen Massebezug. Die folgende Schaltung hat bei sehr niedrigen Frequenzen den Verstärkungsfaktor 1. Der OPV arbeitet als nicht invertierender Verstärker und die Phasenlage beträgt φ ≈ 0°. Für sehr hohe Frequenzen ist der Blindwiderstandswert des Kondensators sehr klein und der nicht invertierende Eingang des OPV liegt praktisch gegen Masse. Der OPV arbeitet als invertierender Verstärker mit dem Verstärkungsfaktor 1. Die Phasenlage des Ausgangssignals geht gegen φ ≈ 180°. Für alle anderen Frequenzen bleibt der Verstärkungsfaktor 1 erhalten.

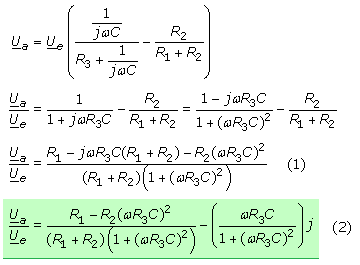
Phasenlaufzeit

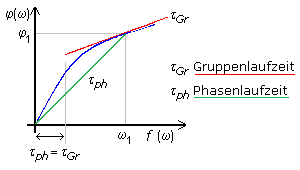
Das Signal erfährt beim Durchlaufen des Filters eine Phasenverschiebung. Für den Allpass wurde diese Abhängigkeit des Phasenwinkels von der Signalfrequenz gemessen. Das Ergebnis ist im Diagramm dargestellt, wobei die Phasenlaufzeit mit angegeben ist. Als Phasenlaufzeit wird der negative Phasengang bezogen auf die Kreisfrequenz ω bezeichnet. \[\left| {{\tau _{ph}}} \right| = - \frac{{\varphi (\omega )}}{\omega }\] Es ist die Verzögerung, die eine monofrequente harmonische Schwingung durch das System erfährt. Sie ist nicht gleich dem Zeitäquivalent der Phasenverschiebung. Ändert sich der Phasenwinkel linear mit der Frequenz, so ist die Phasenlaufzeit konstant und das Ausgangssignal weist dann gegenüber dem Eingangssignal keine Phasenverzerrungen auf.

Gruppenlaufzeit

Die Zeitverzögerung eines schmalbandigen Signals beim Durchlaufen eines Filters ist von der Gruppenlaufzeit bestimmt. Sie ist die Ableitung des Phasengangs nach der Kreisfrequenz und stellt für jede Frequenz die Steigung der Kurve in diesem Punkt dar. \[\left| {{\tau _{Gr}}} \right| = - \frac{{d\varphi (\omega )}}{{d\omega }}\] Sind die Phasen- und Gruppenlaufzeiten unterschiedlich, dann ergeben sich Signalverzerrungen beim Durchlaufen des Filters. Die Phasenlaufzeit ist die Steigung der Gerade vom Ursprung mit ω = 0 zum Kurvenpunkt bei ω. Die Gruppenlaufzeit ist die Steigung der Tangente im Kurvenpunkt bei ω.

Für Leitungssysteme kann eine Phasengeschwindigkeit als Quotient der Leitungslänge und der Phasenlaufzeit angegeben werden, darin ist λ die Wellenlänge des Signals: \[{v_{ph}} = \frac{l}{{{\tau _{ph}}}}\quad mit\quad {v_{ph}} = f \cdot \lambda \]