Lineare Widerstandsnetzwerke
In vielen Schaltungen sind Zweipolelemente sowohl parallel als auch in Reihe geschaltet. Diese gemischten, teilweise umfangreichen Schaltungen werden als Netzwerke bezeichnet. Durch geeignete Methoden lassen sich alle Spannungen und Ströme in diesen Schaltungen berechnen. Nachfolgend sollen nur Schaltungen mit linearen Zweipolelementen beschrieben werden. Zwei der Verfahren sind um 1847 vom Physiker Kirchhoff als Knotensatz und Maschensatz aufgestellt wurden. Die Gesetze der Reihen- und Parallelschaltung sind zu beachten.
Zweipolelemente liegen in Reihe, wenn sie vom selben Strom durchflossen werden.
Zweipolelemente liegen parallel zueinander, wenn sie an derselben Spannung liegen.
Passive Widerstandsnetze
Eine Schaltung ohne angeschlossene Spannungs- oder Stromquelle wird als passiv bezeichnet. Sie kann lineare Bauelemente (Zweipole wie Wirkwiderstände) in gemischter Reihen- und Parallelschaltung enthalten. Nach der Wahl von zwei Anschlussklemmen kann die Schaltung auf einen dazwischen geschalteten Ersatzwiderstand vereinfacht werden. Das folgende Netzwerk wird nach diesen Richtlinien hin untersucht und vereinfacht. Die links angeschlossene DC-Spannungsquelle kann als nicht vorhanden angenommen werden.
Die Widerstände R2 und R3 bilden eine Reihenschaltung durch die nur ein bestimmter Strom fließen kann. Gleiches gilt für die Widerstände R4 und R5 für einen anderen Teilstrom. Die Widerstände R7 und R8 liegen parallel zueinander. An ihnen kann nur eine bestimmte Spannung gemessen werden. Für diese einzelnen Gruppen werden schrittweise Ersatzwiderstände berechnet, um die Schaltung zu vereinfachen. Der Vorgang wird solange wiederholt, bis sie auf einen Gesamtwiderstand reduziert ist. Das schrittweise Berechnen ist einfacher als das Aufstellen einer Gesamtformel.
Mit den Radiobuttons lassen sich die einzelnen Schritte darstellen:
R-Netzwerk
1. Schritt
2. Schritt
3. Schritt
4. Schritt
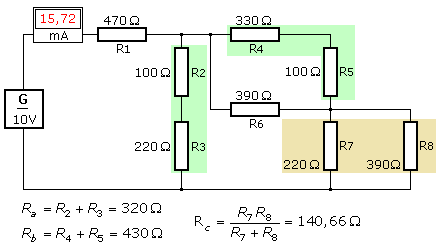
Nach dem 4. Schritt ist das Netzwerk auf eine einfache Reihenschaltung reduziert. Der Gesamtwiderstandswert mit Rges ≈ 636 Ω ist der Wert, der nach dem Ohm'schen Gesetz bei der anliegenden Spannung und dem gemessenen Gesamtstrom errechnet werden kann.
Aktive lineare Netzwerke
Viele Netzwerke haben zusätzlich zu passiven Zweipolelementen auch aktive Zweipole wie Spannungs- und Stromquellen. Oftmals sollen nur bestimmte Spannungen oder Teilströme errechnet werden. In den folgenden Netzwerkanalysen werden einfache lineare Netzwerke behandelt, die sich mithilfe der Ohm'schen Gesetze der Gleichspannung berechnen lassen.
Im normalen Sprachgebrauch besteht ein Netz aus miteinander verknüpften Maschen, deren Verbindungsstellen als Knoten bezeichnet werden. Elektronische Schaltungen mit diversen Baugruppen können als Netz interpretiert werden, wenn mehrere in sich geschlossene Maschen über leitende Knotenpunkte miteinander in Verbindung stehen. Ein Knotenpunkt führt immer zu einer Stromverzweigung.
Knotenpunkte
Ein Knoten(punkt) ist ein elektrisch leitender Verbindungspunkt zwischen mehreren Zweigen und folglich ein Stromverzweigungspunkt. Im Knoten wird weder Strom erzeugt noch gespeichert oder in andere Energieformen umgesetzt. Hat ein Netzwerk k Knotenpunkte, dann lassen sich (k−1) voneinander unabhängige Knotenpunktgleichungen aufstellen. Die Knotenpunktregel ist nach Kirchhoff benannt und sagt aus, dass die Stromsumme im Knoten null ist: \[\sum\limits_{n = 1}^z {{I_n}} = 0\quad \quad z = Zweig\]
- 1. Kirchhoffsche Regel
- Für jeden Knoten ist die Summe der zufließenden Ströme gleich der Summe der abfließenden Ströme.
Als Zweig wird die elektrische Verbindung zwischen zwei Knoten bezeichnet. Im Zweig fließt ein bestimmter Strom. Die Skizze zeigt ein Netzwerk in rein geometrischer Darstellung mit allen Knoten und Zweigen zwischen zwei verschiedenen Knoten. Es gibt 4 Knoten und farblich gekennzeichnet 6 Zweige mit ihrem gleichnummerierten Zweigstrom. Diese Darstellung wird als Streckenkomplex bezeichnet und ist ein reines Schaltbild ohne Schaltelemente. Da in den Zweigen die Stromrichtung vorgegeben ist, handelt es sich um einen gerichteten Graph. Die Stromrichtungen sind frei wählbar, solange jeder Knoten zufließende als auch abfließende Ströme hat, um die Stromknotenregel nach Kirchhoff zu erfüllen.
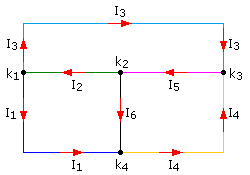
Für jeden Knoten kann eine Knotengleichung geschrieben werde. Per Definition erhalten zufließende Ströme ein positives, abfließende Ströme ein negatives Vorzeichen und die Stromsumme ist null. \[\begin{array}{l} {k_1}\quad {I_2} - {I_1} - {I_3} = 0\\ {k_2}\quad {I_5} - {I_2} - {I_6} = 0\\ {k_3}\quad {I_3} + {I_4} - {I_5} = 0\\ {k_4}\quad {I_1} + {I_6} - {I_4} = 0 \end{array}\] In diesem Gleichungssystem gibt es k−1 voneinander unabhängige Knotengleichungen. Wird die Summe der ersten drei Knotengleichungen gebildet und das Ergebnis mit (−1) multipliziert, so ergibt sich die vierte Knotengleichung. Die Summe der Knotengleichungen 2 ... 4 multipliziert mit (−1) führt zur ersten Knotengleichung und so weiter. Für ein Netzwerk mit k Knoten gibt es wie weiter oben erwähnt genau (k−1) linear unabhängige Knotengleichungen.
Zweige und Maschen
Befindet sich zwischen zwei Netzwerkknoten mindestens ein Zweipolelement, so wird diese Verbindung als Zweig bezeichnet. Im Folgenden werden als Zweipolelemente nur lineare Widerstände, Energiequellen oder deren Reihenschaltungen angenommen. In jedem Zweig fließt ein bestimmter Strom. Alle im Netzwerk vorhandenen Spannungen und Ströme stehen in Beziehungen. Sie können mit den vom Physiker Kirchhoff aufgestellten Knoten- und Maschensätzen mathematisch bestimmt werden. Befindet sich eine ideale Stromquelle im Zweig, so gilt der Zweig als aufgetrennt (unterbrochen) weil die ideale Stromquelle per Definition einen unendlich hohen Innenwiderstand hat. Ein in Reihe zur idealen Stromquelle geschalteter Widerstand wird ebenso vernachlässigt. Reale Stromquellen werden in äquivalente Spannungsquellen umgerechnet.
Eine Netzwerkmasche ist ein in sich geschlossener Umlauf miteinander verbundener Zweige. Der Umlauf beginnt an einem Knoten oder beliebig gewählten Schaltungspunkt und endet dort wieder. Sind im Zweig einzelne Elemente in Reihe geschaltet, so können an ihnen unterschiedliche Spannungsfälle auftreten. Jeder Maschenumlauf verbindet mindestens zwei Zweige mit ihren Zweipolen. Der Umlaufsinn einer Masche kann frei gewählt werden. Die Richtung eines Spannungspfeils am Wirkwiderstand ist identisch mit dem Strompfeil im Zweig. Der Spannungspfeil einer Quelle ist frei wählbar, wobei es oft Sinn macht ihn vom Plus- zum Minuspol zu definieren. Zeigen beim Maschenumlauf einzelne Spannungspfeile entgegen der Umlaufrichtung, so erhalten diese Spannungen ein negatives Vorzeichen.
Beim Maschenumlauf bleibt die Energie erhalten. Der Ladungstransport im Wirkwiderstand erfolgt in Richtung des elektrischen Feldes vom höheren zum niedrigeren Potenzial. Beginnt der Maschenumlauf am positiven Pol und endet am negativen Pol der Spannungsquelle, dann entsprechen die Spannungspfeile dem Erzeuger- und Verbraucherpfeilsystem. Es gilt die von Kirchhoff aufgestellte 2. Regel, bekannt als Maschenregel: \[\sum\limits_{n = 1}^m {{U_n} = 0\quad oder\quad \sum\limits_{n = 1}^m {{I_n} \cdot {R_n}} } = 0\]
- 2. Kirchhoffsche Regel
- In einer geschlossenen Masche ist die Summe aller Teilspannungen gleich null.
- Die Summe der elektromotorischen Kräfte oder idealen Quellenspannungen ist gleich der Summe der Spannungen, die beim Ladungstransport an den Widerständen entstehen (Spannungsfälle).
Der vollständige Baum
Der Begriff gehört zur Topologie (Lage und Anordnung) im Netzwerk. Ein Netzwerkbaum hat eine Anzahl von k Knoten und z Zweigen. Durch jeden Zweig fließt ein bestimmter Strom. Zwischen zwei Knoten befindet sich mindestens ein Netzwerkelement (Zweipol) oder eine Reihenschaltung mehrerer Elemente. Eine ideale Stromquelle zwischen zwei Knoten wird nicht berücksichtigt und gilt nicht als Zweig. Der vollständige Baum ist eine beliebige Verbindung aller Knotenpunkte durch zusammenhängende Baumzweige ohne Maschenbildung. Die im Netzwerk des vollständigen Baums noch offenen Verbindungen zwischen den Knoten sind Verbindungszweige. Die folgende Skizze zeigt ein Netzwerk mit vier Knoten und sechs Zweigen. Rechts sind einige Beispiele zum vollständigen Baum gezeichnet.
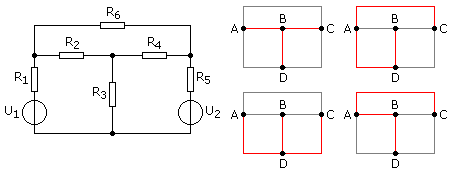
Die Baumzweige sind rot und die Verbindungszweige grau eingezeichnet. Von einem zum anderen Knoten (k) gibt es \(k - 1 = 4 - 1 = 3\) sogenannte Baumzweige als eindeutige Wege durch den Baum. Das Netzwerk ist ein System aus \(z - (k - 1) = 6 - (4 - 1) = 6 - 3 = 3\) unabhängigen Zweigen. Eine Netzwerkmasche ist der geschlossene Umlauf eines Baumzweigs mit genau einem Verbindungszweig. Zur Berechnung des Netzwerks müssen \(z - (k - 1) = z - k + 1 = 6 - 4 + 1 = 3\) unabhängige Maschengleichungen aufgestellt werden. Die Berechnung aller Ströme und Spannungen dieses Netzwerks erfolgt mithilfe eines linearen Gleichungssystem (LGS) aus den unabhängigen 3 Maschen- und 3 Knotengleichungen.
Zweigstromverfahren
Einfache Netzwerke können mit den Strom- und Spannungsgleichungen nach der 1. und 2. Regel von Kirchhoff ohne zu viel mathematischen Aufwand berechnet werden. Im folgenden Netzwerk mit zwei unterschiedlichen Spannungsquellen und linearen Wirkwiderständen sollen alle Spannungen und Zweigströme ermittelt werden. Es gibt 2 Knoten, 3 Zweige und 3 Zweigströme. Nach der Methode des vollständigen Baum sind zur Berechnung eine unabhängige Knotengleichungen und zwei unabhängige Maschengleichungen für das LGS notwendig. Die Strompfeile der Zweige sind frei gewählt eingezeichnet und die Spannungspfeile der beiden DC-Quellen entsprechen dem sogenannten Erzeugerpfeilsystem von Plus nach Minus.
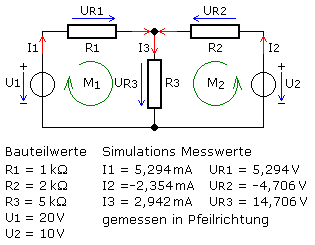
Die Knotengleichung wird bevorzugt für den Knoten aufgestellt, wo die meisten zu bestimmenden Ströme zusammenfließen. Ausgewählt wird der obere Knoten. Der Umlaufsinn der zwei Maschen soll jeweils beim Pluspol einer Quelle beginnen, führt zum oberen Knoten, weiter durch den mittleren Widerstand zum unteren Knoten, weiter zum Minuspol der Startquelle und schließt den Maschenumlauf am Startpunkt. Die Spannungen in den Maschengleichungen werden mithilfe des Ohm'schen Gesetzes durch den jeweiligen Zweigstrom und Widerstand ersetzt. Es ergeben sich drei Gleichungen: \[\begin{array}{l} {I_1} + {I_2} - {I_3} = 0\quad \Rightarrow \quad {I_3} = {I_1} + {I_2}\\ {R_1}\,{I_1} + {R_3}\,{I_3} - {U_1} = 0\quad \Rightarrow \quad {R_1}\,{I_1} + {R_3}\,{I_3} = {U_1}\\ {R_2}\,{I_2} + {R_3}\,{I_3} - {U_2} = 0\quad \Rightarrow \quad {R_2}\,{I_2} + {R_3}\,{I_3} = {U_2} \end{array}\]
Das lineare Gleichungssystem enthält in den drei unabhängigen Gleichungen die drei unbekannten Ströme. Sie können mithilfe des Eliminierungsverfahrens nach Gauß berechnet werden. Die Knotengleichung wird nach I3 umgestellt und in beide Maschengleichungen eingesetzt: \[\begin{array}{l} {R_1}\,{I_1} + {R_3}\,({I_1} + {I_2}) = {U_1}\\ {R_2}\,{I_2} + {R_3}\,({I_1} + {I_2}) = {U_2} \end{array}\] Die Klammerausdrücke werden aufgelöst und durch Ausklammern der Ströme neu sortiert: \[\begin{array}{l} Gl.1\quad ({R_1} + {R_3}) \cdot {I_1} + {R_3} \cdot {I_2} = {U_1}\\ Gl.2\quad {R_3} \cdot {I_1} + ({R_2} + {R_3}) \cdot {I_2} = {U_2} \end{array}\] Die Gleichung Gl.1 wird mit (R2+R3) und die Gleichung Gl.2 mit R3 erweitert. \[\begin{array}{l} ({R_1} + {R_3})({R_2} + {R_3})\,{I_1} + {R_3}({R_2} + {R_3})\,{I_2} = ({R_2} + {R_3})\,{U_1}\\ {R_3} \cdot {R_3} \cdot {I_1} + {R_3}({R_2} + {R_3})\,{I_2} = {R_3} \cdot {U_2} \end{array}\] Wird die zweite von der ersten Gleichung subtrahiert, dann ist der Ausdruck mit dem Strom I2 eliminiert. Es wird nach I1 aufgelöst. \[\begin{array}{l} ({R_1} + {R_3})({R_2} + {R_3})\,{I_1} - {R_3}\,{R_3}\,{I_1} = ({R_2} + {R_3})\,{U_1} - {R_3}\,{U_2}\\ ({R_1}{R_2} + {R_1}{R_3} + {R_2}{R_3} - {R_3}{R_3})\,{I_1} = ({R_2} + {R_3})\,{U_1} - {R_3}\,{U_2} \end{array}\] Das Ergebnis ist die Bestimmungsgleichung für I1: \[{I_1} = \frac{{({R_2} + {R_3}) \cdot {U_1} - {R_3} \cdot {U_2}}}{{{R_1}\,{R_2} + {R_1}\,{R_3} + {R_2}\,{R_3}}}\quad \quad {I_1} = 5,294\,mA\] Zur Berechnung von I2 kann der Wert I1 in Gl.1 oder Gl.2 eingesetzt werden. Um die allgemeine Bestimmungsgleichung für I2 zu erhalten, wird Gl.1 mit R3 und Gl.2 mit (R1+R3) erweitert. Die erste Ergebnisgleichung wird von der zweiten subtrahiert und der Ausdruck mit I1 ist eliminiert. Es wird nach I2 aufgelöst: \[{I_2} = \frac{{({R_1} + {R_3}) \cdot {U_2} - {R_3} \cdot {U_1}}}{{{R_1}\,{R_2} + {R_1}\,{R_3} + {R_2}\,{R_3}}}\quad \quad {I_2} = - 2,353\,mA\] Der Strom I3 errechnet sich mithilfe der Knotengleichung: \[{I_3} = {I_1} + {I_2}\quad \quad {I_3} = 5,294\,mA - 2,353\,mA = 2,941\,mA\] Die Teilspannungen errechnen sich zu: \[\begin{array}{l} {U_{Rn}} = {I_n} \cdot {R_n}\\ {U_{R1}} = 5,294{\mkern 1mu} V\;\;\,{U_{R2}} = - 4,706{\mkern 1mu} V\;\;\,{U_{R3}} = 14,705{\mkern 1mu} V \end{array}\] Die oben beim Netzwerk eingetragenen Werte bestätigen die berechneten Ergebnisse.
Für umfangreichere Netzwerke nimmt der Rechenaufwand erheblich zu, selbst wenn nur einige wenige Teilgrößen berechnet werden sollen. Für das Zweigstromverfahren müssen alle Bestimmungsgleichungen aufgestellt und mathematisch genutzt werden.
Sind Matrizen und Determinanten mit ihren Rechengesetzen nicht ganz unbekannt, so kann das Gleichungssystem mit dem Aufstellen der Koeffizientenmatrix übersichtlicher gelöst werden. Viele wissenschaftliche Taschenrechner verfügen über die Algorithmen und geben die gewünschten Ergebnisse aus. Das Internet bietet kostenfrei nutzbare Onlinerechner, die nach Eingabe der Matrixwerte die Lösungswerte ausgeben. Das einfache Beispielnetzwerk soll mithilfe der Cramerschen Regel berechnet werden.
In den für das Netzwerk aufgestellten Knoten- und Maschengleichungen werden die Teilspannungen an den Widerständen nach dem Ohm'schen Gesetz ersetzt. Die drei Gleichungen werden nach den Indizes der Ströme sortiert. Die Koeffizienten werden in eine quadratische 3x3 Matrix geschrieben und mit dem Spaltenvektor der drei Ströme multipliziert. Gibt es keinen Koeffizienten, dann wird 0 in die Matrix eingetragen. Das Ergebnis nach dem Gleichheitszeichen ist der Ziel- oder Spaltenvektor mit den Spannungswerten. Mit den drei Ausgangsgleichungen entsteht die folgende Matrixdarstellung: \[\begin{array}{l} Gl.I\quad {I_1} + {I_2} - {I_3} = 0\\ Gl.II\quad {R_1} \cdot {I_1} + 0 + {R_3} \cdot {I_3} = {U_1}\\ Gl.III\quad 0 + {R_2} \cdot {I_2} + {R_3} \cdot {I_3} = {U_2}\\ \left( {\begin{array}{*{20}{c}} 1&1&{ - 1}\\ {{R_1}}&0&{{R_3}}\\ 0&{{R_2}}&{{R_3}} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {{I_1}}\\ {{I_2}}\\ {{I_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0\\ {{U_1}}\\ {{U_2}} \end{array}} \right) \end{array}\] Im Gegensatz zu rein mathematischen LGS haben hier die Bauteilwerte eigene Benennungen. Um den Überblick nicht zu verlieren werden sie mit in die Koeffizientenmatrix eingetragen. Die zugehörige Determinante D kann direkt nach der Regel von Sarrus berechnet werden: \[D = \left| {\begin{array}{*{20}{c}} 1&1&{ - 1}\\ {{R_1}}&0&{{R_3}}\\ 0&{{R_2}}&{{R_3}} \end{array}} \right| = - 17 \cdot {10^6}\,A \cdot {\Omega ^2}\] Mit den folgenden Hilfsdeterminanten werden später die Teilströme berechnet. In der Determinante D wird nacheinander die jeweilige Spalte durch den Spaltenvektor der Spannungswerte ersetzt. Die 3x3 Hilfsdeterminanten können wieder mithilfe der Regel von Sarrus berechnet werden: \[{D_{I1}} = \left| {\begin{array}{*{20}{c}} {0\,V}&{1\,A}&{ - 1\,A}\\ {20\,V}&0&{5000\,\Omega }\\ {10\,V}&{2000\,\Omega }&{5000\,\Omega } \end{array}} \right| = - 90 \cdot {10^3}\,A \cdot V \cdot \Omega \] \[{D_{I2}} = \left| {\begin{array}{*{20}{c}} {1\,A}&0&{ - 1\,A}\\ {1000\,\Omega }&{20\,V}&{5000\,\Omega }\\ 0&{10\,V}&{5000\,\Omega } \end{array}} \right| = 40 \cdot {10^3}\,A \cdot V \cdot \Omega \] \[{D_{I3}} = \left| {\begin{array}{*{20}{c}} {1\,A}&{1\,A}&0\\ {1000\,\Omega }&0&{20\,V}\\ 0&{2000\,\Omega }&{10\,V} \end{array}} \right| = - 50 \cdot {10^3}\,A \cdot V \cdot \Omega \] Die gesuchten Ströme sind das Ergebnis der jeweiligen Hilfsdeterminante durch die Koeffizientendeterminante: \[{I_1} = \frac{{{D_{I1}}}}{D} = \frac{{ - 90 \cdot {{10}^3}\,A \cdot V \cdot \Omega }}{{ - 17 \cdot {{10}^6}\,A \cdot {\Omega ^2}}} = 5,294\,mA\] \[{I_2} = \frac{{{D_{I2}}}}{D} = \frac{{40 \cdot {{10}^3}\,A \cdot V \cdot \Omega }}{{ - 17 \cdot {{10}^6}\,A \cdot {\Omega ^2}}} = - 2,353\,mA\] \[{I_3} = \frac{{{D_{I3}}}}{D} = \frac{{ - 50 \cdot {{10}^3}\,A \cdot V \cdot \Omega }}{{ - 17 \cdot {{10}^6}\,A \cdot {\Omega ^2}}} = 2,941\,mA\] Die errechneten Werte stimmen mit den Messergebnissen der Simulationsschaltung gut überein. Mit diesen Werten ergeben sich dann wie oben geschrieben die Teilspannungen an den Widerständen.
Maschenstromverfahren
Zur Berechnung werden nur die Maschengleichungen benötigt. Jeder linear unabhängigen Masche wird ein eigener Maschenstrom zugeordnet. Die Stromrichtung ist grundsätzlich frei wählbar. Die Maschenströme sind praktisch nicht messbar und werden auch virtuelle Ströme genannt. Die Pfeilrichtungen der Spannungsquellen werden festgelegt. Das Maschenstromverfahren soll am folgenden Netzwerk veranschaulicht werden. Es gibt zwei Möglichkeiten das LGS zu erstellen.
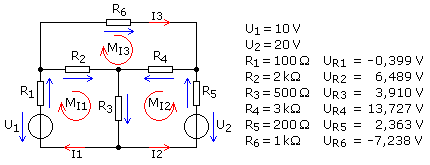
1. Variante
Für jede Masche wird die Maschengleichung aufgestellt. Die nicht bekannten Teilspannungen an den Widerständen der Masche werden nach dem Ohm'schen Gesetz durch das Produkt (R·I) ersetzt.
Da durch einige Widerstände auch zwei unterschiedliche Maschenströme fließen, muss deren Stromrichtung beachtet werden. Es ist also mit der Stromsumme oder Stromdifferenz zu multiplizieren. Befindet sich im Maschenumlauf eine Spannungsquelle mit entgegengesetzter Pfeilrichtung, dann wird ihr Wert subtrahiert und das Ergebnis des Maschenumlaufs ist null.
\[\begin{array}{l}
{M_{I1}}\quad {R_1}\,{I_1} + {R_2}\,({I_1} - {I_3}) + {R_3}\,({I_1} + {I_2}) - {U_1} = 0\\
{M_{I2}}\quad {R_5}\,{I_2} + {R_4}\,({I_2} + {I_3}) + {R_3}\,({I_2} + {I_1}) - {U_2} = 0\\
{M_{I3}}\quad {R_6}\,{I_3} + {R_4}\,({I_3} + {I_3}) + {R_2}\,({I_3} - {I_1}) = 0
\end{array}\]
Das Ergebnis ist ein LGS mit drei Gleichungen und den drei unbekannten Maschenströmen. Im nächsten Schritt werden die Klammern aufgelöst und die drei Ströme neu ausgeklammert:
\[\begin{array}{l}
{M_{I1}}\quad ({R_1} + {R_2} + {R_3})\,{I_1} + {R_3}\,{I_2} - {R_2}\,{I_3} = {U_1}\\
{M_{I2}}\quad {R_3}\,{I_1} + ({R_3} + {R_4} + {R_5})\,{I_2} + {R_4}\,{I_3} = {U_2}\\
{M_{I3}}\quad - {R_2}\,{I_1} + {R_4}\,{I_2} + ({R_2} + {R_4} + {R_6})\,{I_3} = 0
\end{array}\]
Für das LGS folgt die R-Koeffizientenmatrix mit dem Spalten-Zielvektor der Quellenspannungen:
\[\left( {\begin{array}{*{20}{c}}
{{R_1} + {R_2} + {R_3}}&{{R_3}}&{ - {R_2}}\\
{{R_3}}&{{R_3} + {R_4} + {R_5}}&{{R_4}}\\
{ - {R_2}}&{{R_4}}&{{R_2} + {R_4} + {R_6}}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{{U_1}}\\
{{U_2}}\\
0
\end{array}} \right)\]
2. Variante
Mit etwas Übung kann die zweite Möglichkeit etwas schneller zur Lösungsmatrix führen. Für jeden Maschenstrom wird die Summe der durchlaufenen Widerstände aufgeschrieben. In der Koeffizientenmatrix stehen sie auf der Hauptdiagonalen:
\[\begin{array}{l}
{M_{I1}}\quad {R_1} + {R_2} + {R_3}\\
{M_{I2}}\quad {R_3} + {R_4} + {R_5}\\
{M_{I3}}\quad {R_2} + {R_4} + {R_6}
\end{array}\]
Zwischen den einzelnen Maschen befinden sich die sogenannten Koppelwiderstände. Durch sie fließen zwei Maschenströme, deren Richtung zu beachten ist. Im gegebenen Beispiel ist
R2 der Koppelwiderstand zwischen der Masche MI1 und MI3 mit gegenläufigen Stromrichtungen. R3 ist der Koppelwiderstand zwischen MI1 und MI2 mit gleicher Stromrichtung. R4 ist der Koppelwiderstand zwischen
MI2 und MI3 mit gleicher Stromrichtung. Die Koppelwiderstände kommen in der R-Matrix zweimal vor und sind Elemente der Nebendiagonalen. Der Widerstandswert ist negativ einzutragen, wenn die Ströme im durchflossenen Widerstand gegenläufig sind. In die Zielmatrix werden die Quellenspannungen eingetragen. Der Wert ist negativ, wenn ihre Pfeilrichtung gleich dem des Maschenumlaufsinns ist. Mit diesen Angaben hat die R-Koeffizientenmatrix das folgende Aussehen:
\[\left( {\begin{array}{*{20}{c}}
{{R_1} + {R_2} + {R_3}}&{{R_3}}&{ - {R_2}}\\
{{R_3}}&{{R_3} + {R_4} + {R_5}}&{{R_4}}\\
{ - {R_2}}&{{R_4}}&{{R_2} + {R_4} + {R_6}}
\end{array}} \right)\]
Das Ergebnis ist identisch mit dem nach dem ersten Verfahren. Die Matrix ist richtig, wenn die Elementwerte zur Hauptdiagonalen symmetrisch sind. Die drei Maschenströme können per Hand mithilfe der Determinanten wie beim Zweigstromverfahren ausführlich gezeigt, mit einem passenden Taschenrechner oder einem online zur freien Verfügung gestellten Rechenverfahren berechnet werden.
Für dieses Beispiel sind die Ergebnisse: \({I_1} = - 3,993\,mA\quad {I_2} = 11,814\,mA\quad {I_3} = - 7,238\,mA\) Damit können die im Netzwerk tatsächlich messbar fließenden Ströme und die Spannungen für die einzelnen Widerständen berechnet werden. Die Teilspannungen an den Widerständen entsprechen den in Pfeilrichtung ermittelten Messwerten der Simulation.
| R in kΩ | R1=0,1 | R2=2 | R3=0,5 | R4=3 | R5=0,2 | R6=1 |
| I in mA | I1=−3,993 | I1−I3=3,245 | I1+I2=7,821 | I2+I3=4,576 | I2=11,814 | I3=−7,238 |
| U in V | −0,399 | 6,489 | 3,911 | 13,728 | 2,363 | −7,238 |
Knotenpotenzialverfahren
Dieses Verfahren eignet sich zur mathematischen Analyse aller Netzwerke und wird von der im Hintergrund ablaufenden programmierten Berechnung in Simulationsprogrammen eingesetzt. Diese Programme können keine Formelumstellungen vornehmen und es muss nicht überprüft werden, ob eine lineare Unabhängigkeit der Lösungsgleichungen besteht. Für ein zu analysierendes Netzwerk wird ein Bezugsknoten Ko gewählt, der eine Verbindung mit den meisten aller Widerstände hat. Alle anderen Knoten werden fortlaufend nummeriert. Der Bezugsknoten erhält das Potenzial \({\varphi _o} = 0\,V\). Alle anderen Knoten haben ihr eigenes unabhängiges Potenzial. Die Potenzialdifferenz zwischen zwei Knoten ist der messbare Spannungswert.
Die Spannung zwischen dem Knoten K1 und dem Bezugsknoten Ko ist die Spannung \({U_{10}} = {\varphi _{_1}} - {\varphi _0}\) und die Spannung zwischen dem Knoten K1 und K2 ist die Spannung \({U_{12}} = {\varphi _1} - \varphi _2\). Die Pfeilrichtung der Spannung geht vom Startpunkt, dem ersten Index zum Endpunkt, dem zweite Index und damit den Spannungswert an.
Im nächsten Schritt werden alle realen Spannungsquellen in reale Stromquellen umgewandelt. Der in Reihe liegende Innenwiderstand Ri der Spannungsquelle behält seinen Wert und liegt parallel zur Stromquelle. Sie liefert den maximalen Kurzschlussstrom: \({I_{\max }} = {U_{leer}}:{R_i}\). Danach werden alle Widerstände R in ihre Leitwerte G (Kehrwerte) umgerechnet. Nach diesen Vorbereitungen kann das LGS zur Netzwerkberechnung in Matrixform aufgestellt werden. Das folgende Netzwerk wird mithilfe des Knotenpotenzialverfahrens berechnet.
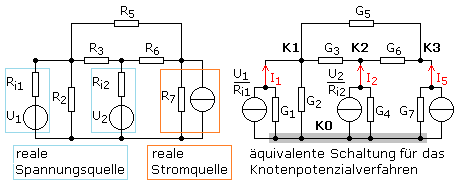
Auf der Hauptdiagonalen der 3x3-Matrix wird die Summe der Leitwerte eingetragen, die mit einem der Knoten K1 ... K3 verbunden sind. Der Knoten K1 ist mit G1, G2, G3 und G5 verbunden. Der Knoten K2 verbindet G3, G4 und G6. Der Knoten K3 verbindet G5, G6 und G7.
Auf den Nebendiagonalen stehen die Leitwerte, die zwischen den Knoten i und j liegen. Sie werden mit negativem Vorzeichen eingetragen und erscheinen in der Matrix zweimal. Zum Beispiel verbindet der Leitwert G3 die Knoten K1 mit K2 ebenso wie K2 mit K1. Die Matrixeinträge sind dann korrekt, wenn die Werte zur Hauptdiagonalen symmetrisch sind. Die Leitwertmatrix hat die folgenden Einträge: \[\left( {\begin{array}{*{20}{c}} {{G_1} + {G_2} + {G_3} + {G_5}}&{ - {G_3}}&{ - {G_5}}\\ { - {G_3}}&{{G_3} + {G_4} + {G_6}}&{ - {G_6}}\\ { - {G_5}}&{ - {G_6}}&{{G_5} + {G_6} + {G_7}} \end{array}} \right)\] Im Lösung- oder Zielvektor werden die Knotenspannungen als Potenzialdifferenz jedes Knotens bezogen auf den Bezugsknoten eingetragen. Im Ergebnisvektor stehen die Ströme. Fließen sie in den Knoten hinein, erhalten sie ein positives Vorzeichen. Aus dem Knoten herausfließende Ströme erhalten ein negatives Vorzeichen. Im gegebenen Beispiel fließen alle Ströme in die drei Knoten hinein. Für die beiden Spaltenvektoren gilt somit: \[Zielvektor\;\left( {\begin{array}{*{20}{c}} {{U_{10}}}\\ {{U_{20}}}\\ {{U_{30}}} \end{array}} \right)\quad Ergebnisvektor\;\left( {\begin{array}{*{20}{c}} {\frac{{{U_1}}}{{{R_1}}}}\\ {\frac{{{U_2}}}{{{R_2}}}}\\ {{I_5}} \end{array}} \right)\]
Das Netzwerk hat die folgenden Komponentenwerte: U1 = 1 V mit Ri1 = 1 Ω, U2 = 2 V mit Ri2 = 5 Ω, I5 = 0,5 A, R2 = 100 Ω, R3 = 200 Ω, R5 = 500 Ω, R6 = 400 Ω und R7 = 10 Ω. Die Leitwerte errechnen sich zu: G1 = 1 S, G2 = 0,01 S, G3 = 0,005 S, G4 = 0,2 S, G5 = 0,002 S, G6 = 0,0025 S und G7 = 0,1 S.
Zur Berechnung stehen in der Matrixform die folgenden Werte: \[\left( {\begin{array}{*{20}{c}} {1,017}&{ - 0,005}&{ - 0,002}\\ { - 0,005}&{0,2075}&{ - 0,0025}\\ { - 0,002}&{ - 0,0025}&{0,1045} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {{U_{10}}}\\ {{U_{20}}}\\ {{U_{30}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ {0,4}\\ {0,5} \end{array}} \right)\] Mit den auf drei Nachkommastellen gerundeten Ergebnissen: \[{U_{10}} = 1,003\,V\quad {U_{20}} = 2,010\,V\quad {U_{30}} = 4,852\,V\] Die Spannungswerte konnten in einer Schaltungssimulation bestätigt werden. Mit den berechneten Knotenpotenzialen können die Spannungen an allen Widerständen des Netzwerks und danach auch die Teilströme durch die Widerstände berechnet werden.
Überlagerungsverfahren nach Helmholtz
Wirken in einem linearen System mehrere Quellen gleichzeitig, dann können alle Teilgrößen berechnet werden, wenn nacheinander jede Quelle einzeln wirkt. Die additive Überlagerung der Einzelergebnisse liefert als Summe die gesuchten Teilgrößen mit allen aktivierten Quellen. Die Methode wird als Überlagerungsverfahren nach Helmholtz oder Superpositionsverfahren bezeichnet. Eine Netzwerkanalyse nach dem Überlagerungsverfahren ist für kleine Netzwerke mit wenigen Elementen sinnvoll und auch dann, wenn nicht alle Teilspannungen und/oder Ströme gesucht sind. Das Verfahren wird an der folgenden Schaltung mit je einer Spannungs- und Stromquelle mit ausschließlich linearen Wirkwiderständen erklärt.
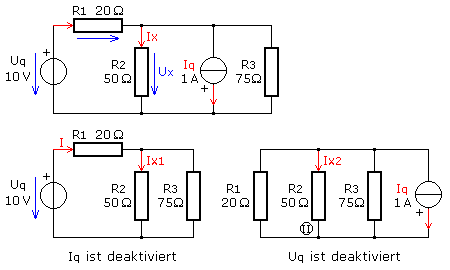
Das Erzeugerpfeilsystem für die Quellen ist von Plus nach Minus festgelegt. In der angegebenen Richtung soll der Strom Ix und der Spannungsfall Ux für den Widerstand R2 berechnet werden. Die Quellen werden nacheinander deaktiviert. Dabei wird die Spannungsquelle zu einem Kurzschluss und die Stromquelle zu einer Unterbrechung. Das gegebene Netzwerk kann in die vereinfachten Schaltungen umgezeichnet werden.
Bei nur aktiver Spannungsquelle fließt der Gesamtstrom I durch R1 und den Parallelwiderstand (R2||R3) und kann berechnet werden: \[\begin{array}{l} {R_{ges}} = {R_1} + \frac{{{R_2}\,{R_3}}}{{{R_2} + {R_3}}} = \left( {20 + \frac{{50 \cdot 75}}{{125}}} \right)\Omega = 50\,\Omega \\ I = \frac{{{U_q}}}{{{R_{ges}}}} = \frac{{10\,V}}{{50\,\Omega }} = 0,2\,A \end{array}\] Mit dem Gesamtstrom I kann die Teilspannung an der Parallelschaltung berechnet werden und damit der Teilstrom Ix1 durch R2: \[\begin{array}{l} {U_{par}} = \frac{{{R_2}\,{R_3}}}{{{R_2} + {R_3}}} \cdot I = 30\,\Omega \cdot 0,2\,A = 6\,V\\ {I_{x1}} = \frac{{{U_{par}}}}{{{R_2}}} = \frac{{6\,V}}{{50\,\Omega }} = 0,120\,A \end{array}\]
Im nächsten Schritt wird die Stromquelle aktiviert und die Spannungsquelle deaktiviert. Ihr Kurzschluss legt R1 parallel zu R2. Der Widerstand R3 liegt ebenfalls parallel an diesen beiden Widerständen. Da der Strom bekannt ist, kann mit dem Gesamtwiderstand die Spannung an der Parallelschaltung berechnet werden. \[\begin{array}{l} {G_{ges}} = {G_1} + {G_2} + {G_3}\\ {G_{ges}} = \frac{1}{{20}}S + \frac{1}{{50}}S + \frac{1}{{75}}S = 83,333\,mS\\ {R_{par}} = \frac{1}{{{G_{ges}}}} = 12\,\Omega \end{array}\] Da der Strom bekannt ist, kann mit dem Gesamtwiderstand die Spannung an der Parallelschaltung berechnet werden. \[U = {R_{par}} \cdot {I_q} = 12\,\Omega \cdot 1\,A = 12\,V\] Der von rechts kommende Strom fließt in den Knoten (II) hinein und würde nach oben aus dem Knoten als Teilstrom Ix2 herausfließen. Die vorgegebene Stromrichtung für Ix ist dazu entgegengesetzt. Der berechnete Teilstrom Ix2 erhält ein negatives Vorzeichen. \[{I_{x2}} = - \frac{U}{{{R_2}}} = - \frac{{12\,V}}{{50\,\Omega }} = - 0,240\,A\]
Mit allen aktivierten Quellen ist der gesuchte Teilstrom Ix für die vorgegebene Stromrichtung die Addition der beiden Teilströme: \[{I_x} = {I_{x1}} + ( - {I_{x2}}) = 120\,mA - 240\,mA = - 120\,mA\] Die Teilspannung Ux in der eingezeichneten Pfeilrichtung am Widerstand R2 beträgt: \[{U_x} = {R_2} \cdot {I_x} = - 50\,\Omega \cdot 120\,mA = - 6\,V\] Die Spannung parallel zum Widerstand R1 würde von links nach rechts gemessen dann +16 V betragen. Alle Ergebnisse können im Laborbetrieb oder mit einer Schaltungssimulation bestätigt werden.