Äquivalente Stern-Dreieck-Umrechnungen

Nicht jedes Widerstandsnetzwerk hat nur parallel oder in Reihe liegende Teilzweige und kann durch einfaches Umzeichnen aufgelöst werden. Ein Hilfsmittel bietet die Stern-Dreieck-Umwandlung. Beide Schaltungsvarianten gibt es in Generatorschaltungen der Stromnetze, in der Antriebstechnik mit leistungsstarken Elektromotoren und in Brückenschaltungen. Bilden drei Widerstände eine Dreieckschaltung, dann kann sie in eine dazu gleichwertige Sternschaltung umgewandelt werden. Die Umwandlung setzt voraus, dass die Verhältnisse zwischen den Klemmen in beiden Schaltungsvarianten gleich bleiben.

Dreieck-Stern-Umwandlung

Die drei Widerstände Rd1, Rd2 und Rd3 bilden eine Dreieckschaltung mit dem Klemmen 1, 2 und 3. Die dazu äquivalente Sternschaltung hat die gleichen Klemmen und die zu bestimmenden Widerstände Rs1, Rs2 und Rs3. Es muss zum Beispiel die Spannung der Dreieckschaltung zwischen den Anschlüssen 1 und 2 gleich der Spannung der Sternschaltung zwischen den Punkten 1 und 2 sein. Ebenso muss der Strom zwischen den betrachteten Anschlüssen in beiden Schaltungsvarianten identisch sein.

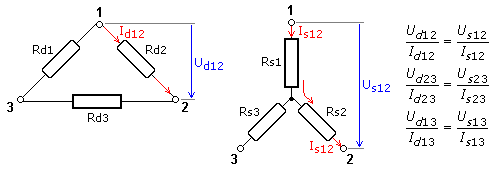
Für die Dreieckschaltung kann zwischen den Punkten 1 und 2 der Gesamtwiderstand Rd12 bestimmt werden. Er errechnet sich aus der Parallelschaltung von Rd2 und der Summe Rd1 + Rd3. In der Sternschaltung ist der gleichwertige Widerstand zwischen den Punkten 1 und 2 der Gesamtwiderstand Rs12 = Rs1 + Rs2. Die beiden Gesamtwiderstände müssen gleiche Werte haben. Für die beiden anderen Punktepaare gelten entsprechende Ansätze.

Man erhält drei Gleichungen und nach einigen Umformungen die Formeln zum Berechnen der drei Widerstandswerte der äquivalenten Sternschaltung. Die Umwandlungsgleichung für den Widerstand, der an einen Punkt der Sternschaltung angeschlossen ist, ergibt sich aus dem Produkt der an diesem Punkt der Dreieckschaltung anliegenden Widerstandswerte geteilt durch die Summe der Widerstandswerte für einen Umlauf im Dreieck.

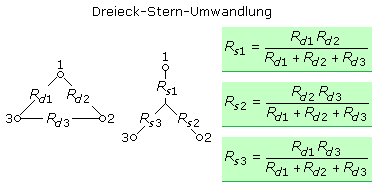
Stern-Dreieck-Umwandlung

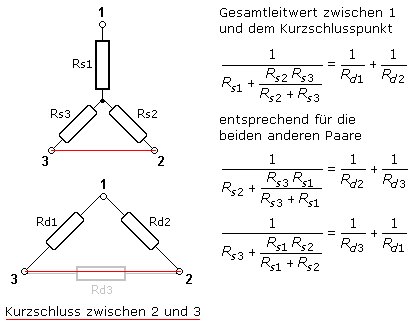
Die Transformation ist auch in umgekehrter Richtung möglich. Die Widerstände Rs1, Rs2 und Rs3 einer Sternschaltung werden in die dazu äquivalenten Widerstände Rd1, Rd2 und Rd3 der Dreieckschaltung umgerechnet. In der Sternschaltung erhält man den Gesamtwiderstand zwischen den Anschlusspunkten 1, 2(3) durch Kurzschluss der Punkte 2 und 3 aus der Summe von Rs1 und der Parallelschaltung aus Rs2 mit Rs3. Da in der äquivalenten Dreieckschaltung die gleichen Punkte kurzgeschlossen sind, ergibt sich dort der Gesamtwiderstand aus der Parallelschaltung der Widerstände Rd1 und Rd2. Für die beiden anderen Anschlusspaare gelten entsprechende Ansätze.

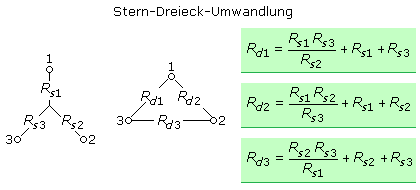
Auch hier gibt es drei Gleichungen mit den drei zu bestimmenden Widerständen der äquivalenten Dreieckschaltung, die nach einigen Umformungen zu den endgültigen Bestimmungsgleichungen führen. Der Widerstandswert zwischen zwei Anschlusspunkten in der Dreieckschaltung errechnet aus dem Produkt der in der Sternschaltung an den Punkten anliegenden Widerstände dividiert durch den verbleibenden Widerstand, dem die beiden Anliegerwiderstände hinzuaddiert werden.

Anwendungsbeispiel – Widerstandsbrücke

Die Gültigkeit der Stern-Dreieck-Umwandlung soll am folgenden Schaltungsnetz aus 5 Widerständen nachgewiesen werden. Es handelt sich um eine nicht abgeglichene Brückenschaltung mit ohmschen Widerständen, deren Gesamtwiderstandswert bestimmt werden soll. Der Brückenwiderstand bildet mit den links davon liegenden Widerständen eine Dreieckschaltung. Sie wird in eine äquivalente Sternschaltung umgerechnet. Das Ergebnis ist dann ein leicht zu überschauendes Widerstandsnetzwerk.

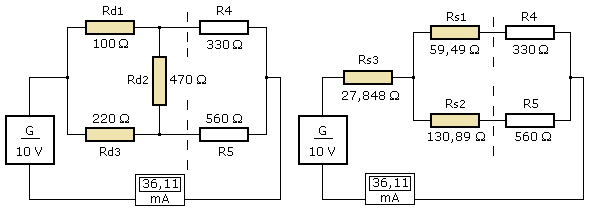
Nach der Umwandlung liegen die Widerstände Rs1 und R4 in Reihe und bilden mit der Reihenschaltung von Rs2 und R5 eine Parallelschaltung. Die beiden Ersatzwerte der Reihenschaltungen sind 389,49 Ω und 690,89 Ω. Der Parallelersatzwert errechnet sich zu 249,07 Ω. Mit dem Reihenwiderstand Rs3 folgen 276,9 Ω für den Gesamtwiderstandswert. Er entspricht dem in der Simulation nach dem ohmschen Gesetz ermittelten Messwert.