Gyratorschaltung mit NIC
Die elektrischen Eigenschaften einer Spule sind verglichen mit einem Kondensator weniger ideal und oft benötigt sie mehr Platz. Sie hat einen meistens nicht zu vernachlässigen ohmschen Drahtwiderstand und im Bereich hoher Frequenzen störende Windungskapazitäten. Eine Spule reagiert auf wechselnde Magnetfelder der Umgebung und generiert Induktionsspannungen, die in nicht speziell geschirmten Schaltungen als Störquellen wirken können. Spulen sind in der Herstellung aufwendig und passen nicht in integrierte Schaltungen. In vielen aktiven Elektronikschaltungen der Kleinsignaltechnik kann die reale Induktivität durch geeignete Hilfsschaltungen, die eine simulierte Induktivität bilden, ersetzt werden. In der Leistungselektronik ist man auf die magnetische Energiespeicherung in Transformatoren und Drosselspulen angewiesen.
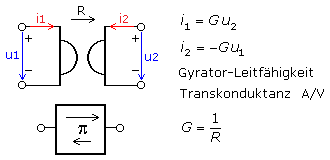
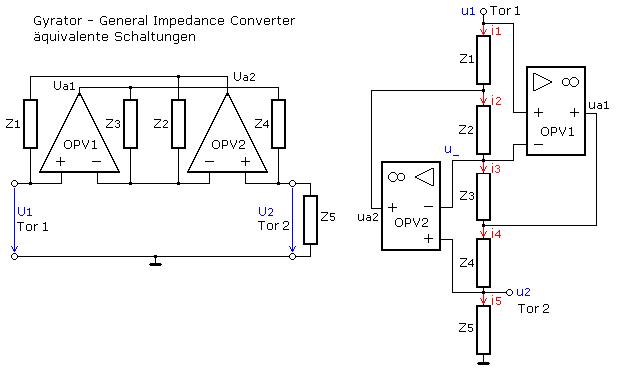
Ein idealer Gyrator ist eine linear arbeitende Übertragerschaltung, die allgemein als Zweitor, ehemals als Vierpol bezeichnet, dargestellt wird. Der gerichtete Übertrag wird als Gyratorwiderstand R, vielfach aber als Gyratorleitfähigkeit G oder Transkonduktanz bezeichnet. Mit ihr wird der am Tor eingespeiste Strom in Pfeilrichtung in eine Spannung am anderen Tor und umgekehrt gewandelt. Eine am Tor in Pfeilrichtung angelegte Spannung wird mit negativem Übertragungsfaktor in einen Strom am Gegentor gewandelt. Als verlustlose Schaltkomponente definiert, ist die unmittelbare Leistungsbilanz des Gyrators gleich null.
Der Gyrator kann als Zweitor-Schaltsymbol oder als lineares Zweipolblockelement dargestellt werden. Die Pfeilspitze zeigt auf das Spannungstor und beginnt am Stromtor. Der Gyrator ist eine duale Phasendrehschaltung, die nur in der längeren Pfeilrichtung eine Phasenumkehr von 180° bewirkt.
Mit integrierten Bauteilen kann die Gyratorschaltung aus zwei Negativ Impedanzkonvertern (NIC), den spannungsgesteuerten Stromquellen, in unterschiedlichen Schaltungsvarianten aufgebaut werden. Zur Herleitung der Übertragungs- oder Transfergleichungen wird ein ideales Verhalten der OPVs angenommen. Es fließen keine Eingangsströme in den OPV und die Differenzspannung zwischen den Eingängen direkt am OPV beträgt 0 Volt. Alle Widerstandswerte sollen gleich sein. Die Teilströme berechnen sich aus den Quotienten der Teilspannungen am jeweiligen Widerstand.
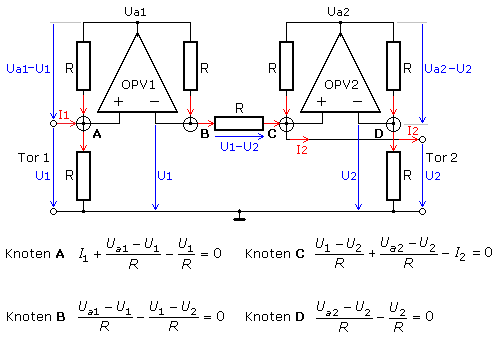
Die für den Gyrator geltende Transfergleichung errechnet sich durch Gleichsetzen der Knotengleichungen A mit B und C mit D wenn diese nach dem Ausdruck mit der OPV-Ausgangsspannung aufgelöst werden.
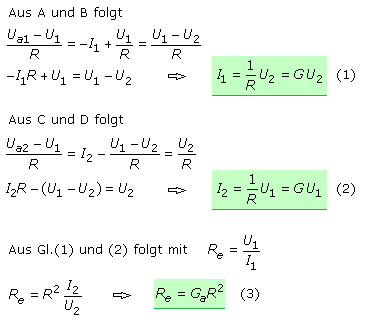
Bei den Herleitungen zum NIC wurde gezeigt, dass die Beziehungen für DC und AC gelten. Die Last kann somit eine Reaktanz, ein idealer Wechselstromwiderstand oder Impedanz, ein komplexer Wechselstromwiderstand sein. Ist in der Gl.(3) anstelle des Lastwiderstands Ra ein kapazitiver Blindwiderstand XC geschaltet, dann nimmt der Gyrator die Eigenschaften einer Induktivität an.
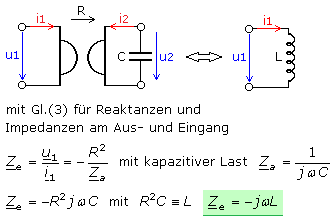
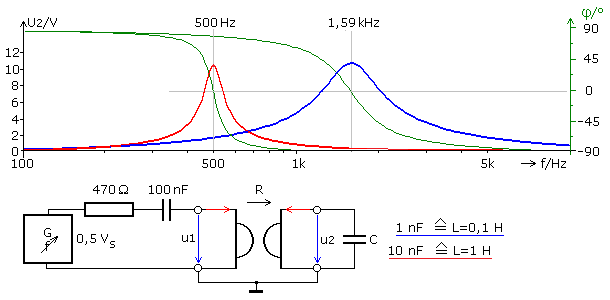
Sowohl im Labor als auch per Simulation konnten mit dieser Idee Schwingkreise mit nachgebildeten Induktivitäten aufgebaut werden. Alle Widerstände waren mit 10 kΩ gleich. Der Eingang wurde mit einem Vorwiderstand und einem Kondensator beschaltet. An den Ausgang wurden Kondensatoren unterschiedlicher Kapazitäten geschaltet. Sie bilden mit der OPV-Schaltung die jeweilige Induktivität, die aus der Transferfunktion errechnet werden kann.
Die folgende Schaltung stellt einen Reihenschwingkreis dar. Die aus den Resonanzfrequenzen ermittelbaren Induktivitätswerte stimmen mit den berechneten Werten überein. Der Vorwiderstand ist für die Bandbreite verantwortlich. Das Diagramm stellt die Ausgangsspannung u2 als Spannungsüberhöhung am Blindwiderstand von C in Abhängigkeit der Eingangsfrequenz dar. Der Kurvenverlauf zeigt den typischen Amplitudenfrequenzgang eines Schwingkreises. Gleiches gilt für den Phasengang (grüne Kurve), der an der Resonanzstelle 0° aufweist.
Allgemeine Gyratorschaltung
Der Gyrator kann in einer ähnlichen Schaltungsvariante vorliegen, die im englischen Sprachgebrauch als General Impedance Converter GIC benannt wird. Zur Herleitung der Transfergleichungen werden die Widerstände anfangs als Impedanzen angesehen. Die beiden OPVs sollen sich ideal verhalten und nehmen keine Eingangsströme auf. Die Spannungsdifferenzen an den OPV-Eingängen sollen den Wert null annehmen. Zur Herleitung der Eingangsimpedanz am Tor 1 ist die rechts dargestellte Schaltungsvariante gut geeignet.
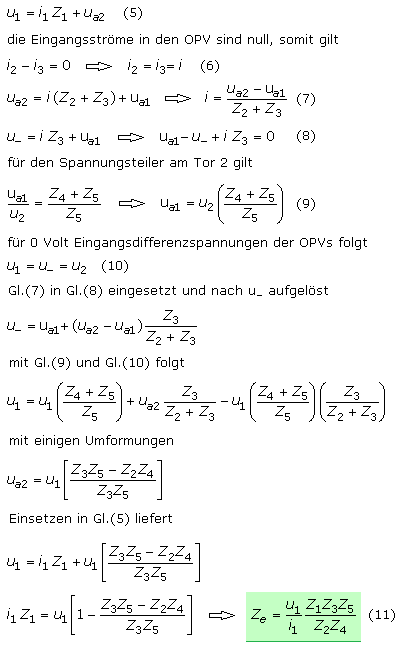
Wird Z2 oder Z4 durch einen kapazitiven Blindwiderstand ersetzt und alle anderen Impedanzen sind ohmsche Widerstände, dann entspricht die Schaltung am Tor 1 einer großen Induktivität.
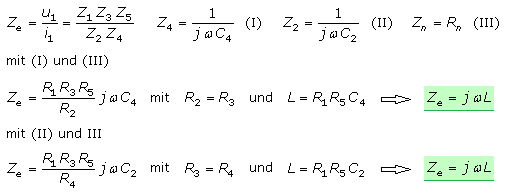
Schaltungssimulationen bestätigen das mathematisch hergeleitete Verhalten. Ein Kondensator mit 22 nF anstelle Z2 oder Z4 mit einem Vorwiderstand von 1 kΩ zeigt in der AC-Frequenzanalyse (Bodediagramm) einen Hochpass 1. Ordnung. Der aus der Grenzfrequenz errechenbare Induktivitätswert stimmt mit dem aus der Gyratortransfergleichung überein.
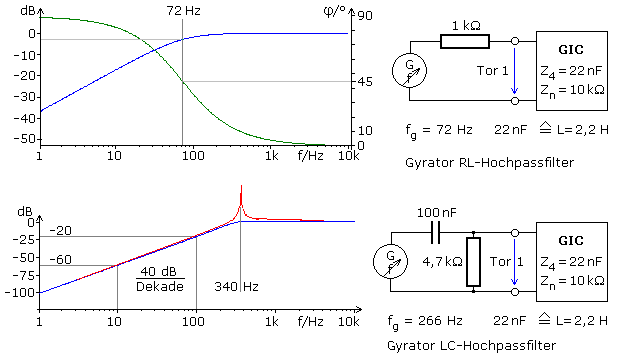
Mit einem zum Tor 1 in Reihe geschalteten Kondensator zeigt das Bodediagramm am Tor 1 den typischen Verlauf eines LC-Filters. Die Steilheit im Sperrbereich beträgt −40 dB/Dekade. Die unbelastete und somit nicht gedämpfte Schaltung zeigt eine Resonanzstelle, deren Resonanzfrequenz mit der aus der Thomsonschen Gleichung übereinstimmt. Der zum Tor 1 parallele Dämpfungswiderstand wurde solange variiert, bis kein Überschwingen mehr erkennbar war. Das Ergebnis ist ein optimaler LC-Hochpass 2. Ordnung ohne reale Spule.