Der Kondensator im Gleichstromkreis
An einer konstanten Gleichspannungsquelle wird über einen realen Vorwiderstand ein Kondensator aufgeladen. Während des Ladevorgangs werden gleichzeitig Strom und Spannung am Kondensator als Funktion der Zeit gemessen. Die Auswertung zeigt, dass innerhalb gleicher Zeitintervalle Strom und Spannung keinen linearen Verlauf haben. Nach der Beschreibung des Widerstandsverhaltens eines Kondensators im Gleichstromkreis folgen Hinweise zu Kondensatoren in Reihenschaltung und Kondensatoren in Parallelschaltung. Während der Ladezeit werden elektrische Ladungen transportiert. Die Ladungsänderung pro Zeitintervall ist gleich dem elektrischen Strom.
Im Zeitintervall (Δt) errechnet sich die durch den Vorwiderstand transportierte Ladungsmenge zu: \[\Delta Q = I(t) \cdot \Delta t\] Der Kondensator wird mit ΔQ etwas aufgeladen, wobei sich seine Spannung um ΔU verändert. \[\Delta Q = C \cdot \Delta U\] Die Ladungen ΔQ sind gleich, also sind auch die rechten Seiten beider Gleichungen gleich. \[I(t) \cdot \Delta t = C \cdot \Delta U\] Der Strom kann durch die Spannung und den Vorwiderstandswert ersetzt werden. \[\frac{{\Delta t \cdot U(t)}}{R} = C \cdot \Delta U\] Wird nach R·C aufgelöst, so hat das Produkt die Dimension der Zeit in s. \[\frac{{\Delta t \cdot U(t)}}{{\Delta U}} = R \cdot C\] R·C ist als Zeitkonstante definiert und erhält den griechischen Buchstaben τ (tau). \[\tau = R \cdot C\]
Die Zeitkonstante
Sie ist unabhängig von Strom und Spannung und sagt etwas über die Geschwindigkeit aus, mit der die Ladevorgänge eines Kondensators in der RC-Reihenschaltung erfolgen. Bei vorgegebener Kapazität dauert die Aufladung umso länger, je größer der Widerstandswert ist. Ebenso dauert der Ladevorgang bei einem größeren Kapazitätswert bei gleichem Vorwiderstand länger. Die Lade- und zugehörigen Entladevorgänge können im folgenden Videoclip für drei unterschiedliche R-C-Kombinationen betrachtet werden.
Der Vorwiderstand R begrenzt den Ladestrom. Wird zum Zeitpunkt t = 0 der Stromkreis geschlossen, so ist die anliegende Quellenspannung nur über dem Widerstand messbar. Bei t = 0 hat der Kondensator noch keine Ladung und mit 0 V keine Spannung. Je mehr Ladung transportiert wird, desto höher wird die Spannung am Kondensator. Da R und C eine Reihenschaltung bilden, muss nach dem Ohm'schen Gesetz die Spannung UR am Widerstand entsprechend kleiner werden. Da R konstant ist, wird bei abnehmender UR auch der Strom geringer. Hat die Spannung am Widerstand den halben Anfangswert, so ist der Ladestrom nur noch halb so groß. Während dieser Zeit t = t1 hat der Kondensator die Ladung \({Q_1} = C \cdot 0,5 \cdot U\) aufgenommen.
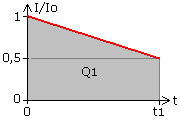
Im Strom-Zeit-Diagramm dargestellt entspricht die Fläche unter der Kurve der Kondensatorladung. Die graue Fläche ist ein Trapez mit dem Flächeninhalt: \[{Q_1} = (1 + 0,5) \cdot 0,5 \cdot {I_o} \cdot {t_1}\] Mit Io gegeben durch U und R kann t1 berechnet werden. Diese Zeit ist die Halbwertszeit th des RC-Glieds. \[{t_1} = 0,667 \cdot R \cdot C = 0,667 \cdot \tau \quad \Rightarrow {t_h} \approx 0,7 \cdot \tau \]
Erfolgt die Aufladung an einer Konstantspannungsquelle, so kann während der ersten Halbwertzeit der Stromverlauf als weitgehend linear angenommen werden. Genau genommen ist der Ladestrom in keinem Abschnitt linear. Der Rundungsfaktor 0,7 eine sehr gute Näherung zum tatsächlichen Stromverlauf. Das folgende Diagramm stellt den genauen Ladevorgang eines Kondensators dar. Nach rund sieben Halbwertzeiten kann für die anliegende Spannung der Kondensator als aufgeladen betrachtet werden. Die exakten Endwerte von 0 % für den Strom und 100 % für die Spannung am Kondensator werden nie erreicht. Beide Kurven nähern sich asymptotisch ihren Endwerten.
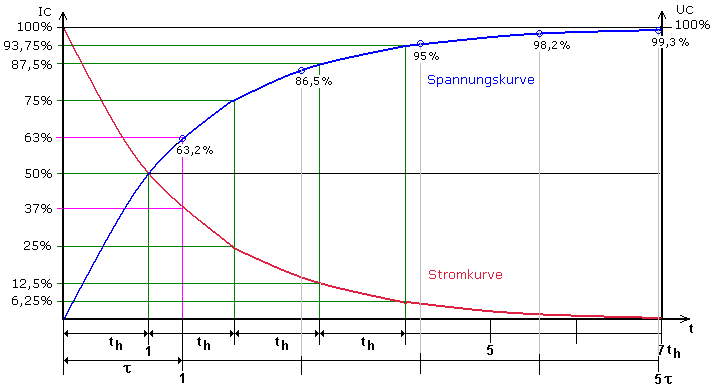
Nach Ablauf einer Halbwertzeit th hat der Ladestrom noch 50 % seines Anfangswerts. Die Spannung am Kondensator ist auf 50 % des Endwerts gestiegen. Nach Ablauf einer weiteren Halbwertzeit hat der Ladestrom auf 25 % abgenommen und die Kondensatorspannung hat 75 % ihres Endwerts erreicht. Die nach der ersten Halbwertzeit verbliebenen 50 % haben sich erneut halbiert. Für jede weitere Halbierung der verbleibenden Prozente vergeht stets eine Halbwertzeit. Nach sieben Halbwertzeiten ist der Ladestrom praktisch auf null gefallen und der Kondensator hat die maximale Spannung erreicht.
Kurvenzüge mit gleich großen Halbwertzeiten werden mathematisch durch natürliche Funktionen, den Exponentialfunktionen, abgekürzt e-Funktionen, beschrieben. Viele Naturvorgänge, wie z. B. der radioaktive Zerfall, Erwärmungs- und Abkühlungsprozesse und biologisches Zellwachstum folgen solchen e-Funktionen.
Auf der Zeitachse ist im Diagramm auch die Zeitkonstante τ des RC-Glieds eingetragen. Nach Ablauf einer Zeitkonstanten 1·τ ist der Ladestrom auf 36,8 % seines Anfangswertes gefallen und die Ladespannung auf 63,2 % ihres Endwertes gestiegen. Nach Ablauf von 5·τ entsprechend sieben Halbwertzeiten 7·th ist der Ladevorgang praktisch beendet. Diese Zeit wird als Einschaltzeit des RC-Glieds bezeichnet.
Für eine Quellenspannung Uo = 100 V soll im ganzzahligen Abstand von τ die jeweilige Ladespannung des Kondensators ermittelt werden. Die Ladekurve im Diagramm oben zeigt, dass nach dem Ablauf einer Zeitkonstante der Kondensator auf 63,2 % also 63,2 V aufgeladen wurde. Die Spannungsdifferenz zur Quellenspannung beträgt dann 36,8 V. Mit dieser Spannung kann der Kondensator innerhalb einer weiteren Zeitkonstanten weiter aufladen kann. Das passiert wieder mit 63,2 % von 36,8 V. Die Kondensatorspannung erreicht nach zwei tau 63,2 V + 23,26 V = 86,5 V. Die Spannungsdifferenz zu den 100 V beträgt noch 13,5 V. Während der dritten Zeitkonstanten lädt diese Restspannung den Kondensator um weitere 63,2 % oder 8,53 V auf und erreicht 95 V. Während der vierten Zeitkonstanten wird der Kondensator mit 63,2 % der Restspannung von 5 V um weitere 3,2 V geladen. Die Ladespannung erreicht den Wert 98,2 V. Zur Quellenspannung bleiben noch 1,8 V, die in der fünften Zeitkonstanten den Kondensator um weitere 63,2 % davon, also 1,14 V aufladen. Nach fünf tau ist der Kondensator auf 99,3 V aufgeladen. Damit ist praktisch die Quellenspannung von 100 V erreicht. Theoretisch mathematisch wird sie nie genau erreicht.
Bei der Entladung verläuft die Strom- und Spannungskurve ebenfalls nach einer e-Funktion. Nach 5·τ sind die Kurven auf unter 1 % ihres Anfangswertes gefallen. Diese Zeit wird Ausschaltzeit des RC-Glieds genannt. Beim Entladen fließt der Strom in entgegengesetzter Richtung durch den Widerstand, da der geladene Kondensator die Spannungsquelle ist und von der äußeren DC-Quelle getrennt ist.
Das Diagramm zeigt, dass beim noch ungeladenen Kondensator im Einschaltmoment der maximale Strom fließt und am Kondensator keine Spannung messbar ist. Nach dem Ohm'schen Gesetz verhält sich der Kondensator wie ein Kurzschluss oder Widerstand mit 0 Ω. Nach der Aufladezeit von 5 ·τ nimmt der Kondensator praktisch keine weitere Ladung auf und der Stromfluss geht gegen null. Im Gleichstromkreis verhält sich der vollständig geladene Kondensator wie ein Widerstand mit extrem hohem Wert vergleichbar mit einer Unterbrechung. Für den Wechselstromwiderstand eines Kondensators gibt es ein eigenes Kapitel.
Im Einschaltmoment verhalten sich ungeladene Kondensatoren wie ein Kurzschluss.
Im Gleichstromkreis verhalten sich auf die Endspannung geladene Kondensatoren wie eine Unterbrechung. Ihr Widerstandswert ist extrem groß.
Innerhalb der Zeitkonstante 1·τ eines RC-Glieds wird ein Kondensator auf 63 % seines Endwertes aufgeladen oder auf 37 % seines Anfangswertes entladen.
Nach 5·τ gilt ein Kondensator als praktisch vollständig auf- bzw. entladen. Diese Zeit wird auch als Einschalt- oder Ausschaltzeit des RC-Glieds bezeichnet.
Der Lade- und Entladevorgang wird durch e-Funktionen beschrieben. Die Halbwertzeit beträgt th = 0,7·τ
Die e-Funktionen des Lade- und Entladevorgangs
In Formelsammlungen zur Elektronik sind die Lade- und Entladefunktionen eines Kondensators an DC-Quellen angegeben. Die Berechnung der zeitlichen Momentanwerte erfolgt mit der Zeitkonstante \(\tau = R \cdot C\) der Schaltung. Der Kondensator wird ab t = 0 an der DC-Quellenspannung Uo geladen. Die Ladung eines Kondensator ist proportional zu seiner Spannung: \({Q_c} = C \cdot {U_c}\) Für den zeitlichen Verlauf der Ladekurven gelten die folgenden Formeln: \[{U_c}(t) = {U_o} \cdot \left( {1 - {e^{ - \frac{t}{{R\,C}}}}} \right)\] \[{I_c}(t) = \frac{{{U_o}}}{R} \cdot {e^{ - \frac{t}{{R\,C}}}}\] \[{Q_c}(t) = C \cdot {U_o} \cdot \left( {1 - {e^{ - \frac{t}{{R\,C}}}}} \right)\] Ist der Ladevorgang nach 5·τ mit praktisch Uo beendet und wird der Kondensator über den gleichen Widerstand entladen, so gelten mit dem Beginn der Entladung bei t = 0 die folgenden Formeln: \[{U_c}(t) = {U_o} \cdot {e^{ - \frac{t}{{R\,C}}}}\] Der Entladestrom fließt in die entgegengesetzte Richtung des Ladestroms. \[{I_c}(t) = - \frac{{{U_o}}}{R} \cdot {e^{ - \frac{t}{{R\,C}}}}\] \[{Q_c}(t) = C \cdot {U_o} \cdot {e^{ - \frac{t}{{R\,C}}}}\]
Mathematische Herleitungen
Aufladung eines Kondensators
Die Herleitungen der e-Funktionen gehen normalerweise über das berufliche duale Ausbildungsniveau hinaus. Es handelt sich um das Lösen von Differentialgleichungen, wobei das Verfahren hier noch gut nachvollziehbar ist. Der Ladestromkreis stellt eine Masche dar. Für einen geschlossenen Maschenumlauf gilt, dass die Summe aller auftretenden Spannungen immer null ist. Beim Ladevorgang fließt ein sich zeitlich ändernder Strom I(t), der mit R multipliziert anstelle UR geschrieben werden kann. Die Spannung am Kondensator ist proportional zur Ladung, somit kann auch UC geeignet ersetzt werden: \[{U_R} + {U_C} - {U_o} = 0\:\quad \Rightarrow {U_o} = R \cdot I(t) + \frac{{Q(t)}}{C}\] Ändert sich die Ladung linear mit der Zeit, dann ist die 1. Ableitung gleich dem sich zeitlich ändernden Strom: \[I(t) = \frac{{\Delta Q}}{{\Delta t}} = \frac{{dQ(t)}}{{dt}}\] Wird die oben nach Uo umgestellte Maschengleichung nach der Zeit t abgeleitet, dann ist das Ergebnis eine homogene lineare Differentialgleichung (DGL). Sie enthält neben der Funktion I(t) auch ihre 1. Ableitung. Die Konstante Uo abgeleitet nach der Zeit ergibt null: \[R\frac{{d(I(t)}}{{dt}} + \frac{1}{C} \cdot I(t) = 0\] Die Ableitung einer Exponentialfunktion ist gleich der Funktion, wenn notwendig multipliziert mit der inneren Ableitung. Der Strom Io ist ein konstanter Anfangswert. \[I(t) = {I_o} \cdot {e^{k\,t}}\quad mit\quad \frac{{d\,I(t)}}{{dt}} = {I_o} \cdot k \cdot {e^{k\,t}}\] Beide Formeln in die DGL eingesetzt ergeben: \[R \cdot {I_o} \cdot k \cdot {e^{k\,t}} + \frac{1}{C} \cdot {I_o} \cdot {e^{k\,t}} = 0\] Nach dem Ausklammern kann die Konstante k sehr leicht berechnet werden: \[{I_o} \cdot {e^{kt}}\left( {R \cdot k + \frac{1}{C}} \right) = 0\quad \Rightarrow k = - \frac{1}{{R\,C}} = - \frac{1}{\tau }\] In die oben gewählte allgemeine Exponentialfunktion eingesetzt und Io durch die Ladespannung Uo und den Vorwiderstand R ersetzt ist das Ergebnis die Formel für den Ladestromverlauf: \[I(t) = \frac{{{U_o}}}{R} \cdot {e^{ - {\textstyle{t \over \tau }}}}\] Die zeitliche Änderung der Spannung am Kondensator UC(t) kann mithilfe der Maschengleichung und des Ladestroms hergeleitet werden. In der Reihenschaltung fließt der gleiche Ladestrom durch den Widerstand R und verursacht dort die sich zeitlich ändernde Spannung. Nach kurzer Umformung folgt die Formel für den Spannungsverlauf am Kondensator. \[{U_C}(t) = {U_o} - {U_R}(t) = {U_o} - R \cdot \frac{{{U_o}}}{R} \cdot {e^{ - \frac{t}{\tau }}}\] \[{U_C}(t) = {U_o}\left( {1 - {e^{ - \frac{t}{\tau }}}} \right)\]
Entladung eines Kondensators
Die mathematischen Herleitungen der Entladeformeln verlaufen ähnlich. Der Kondensator ist auf die Spannung UC aufgeladen und wird über den Widerstand R entladen. Die Ladung Q ist proportional zur Spannung UC. Der Entladestrom I(t) ist die 1. Ableitung der Ladung Q nach der Zeit und erzeugt die proportionale Spannung UR. Im Maschensatz sind die Spannungswerte gleich und unterscheiden sich nur im Vorzeichen. \[{U_C}(t) = - {U_R}(t)\quad mit\quad {U_C}(t) = \frac{{Q(t)}}{C}\] \[\frac{{Q(t)}}{C} + R \cdot I(t) = 0\;\;\,mit\;\;\,I(t) = \frac{{dQ(t)}}{{dt}}\] \[\frac{{Q(t)}}{C} + R \cdot \frac{{dQ(t)}}{{dt}} = 0\quad \Rightarrow \frac{1}{{R\,C}} \cdot Q(t) + \frac{{dQ(t)}}{{dt}} = 0\] Das Ergebnis ist eine lineare homogene Differentialgleichung, mit der Funktion Q(t) und ihrer Ableitung. Ein Lösungsansatz gelingt mithilfe einer Exponentialfunktion: \[Q(t) = {Q_o} \cdot {e^{ - k\,t}}\quad \Rightarrow \frac{{dQ(t)}}{{dt}} = - k \cdot {Q_o} \cdot {e^{ - k\,t}}\] Durch Einsetzen in die DGL und Umformen kann k bestimmt werden: \[\frac{1}{{R\,C}} \cdot {Q_o} \cdot {e^{ - k\,t}} = - \left( { - k \cdot {Q_o} \cdot {e^{ - k\,t}}} \right)\quad \Rightarrow k = \frac{1}{{R\,C}}\] Einsetzen von k in die Funktion Q(t) ergibt mit den Proportionalitäten zur Spannung und der Zeitkonstante tau die Entladefunktion: \[Q(t) = {Q_o} \cdot {e^{ - \frac{t}{{R\,C}}}}\quad \Rightarrow {U_C}(t) = {U_o} \cdot {e^{ - \frac{t}{\tau }}}\] Zum Beginn der Entladung hat der Kondensator die Ladespannung Uo und stellt jetzt die Spannungsquelle dar. Beim Entladevorgang fließt der entgegengesetzte Ladestrom über den Widerstand: \[{I_C}(t) = - \frac{{{U_o}}}{R} \cdot {e^{ - \frac{t}{\tau }}}\] Der Exponentialausdruck hat für \(t = 5\,\tau \) den Wert 45,4 μs ist also praktisch null. Der Kondensator gilt als entladen und ohne Spannung fließt auch kein Strom.
△