Widerstände im Wechselstromkreis
Der Wirkwiderstand
Von den drei passiven Bauteilen Widerstand, Kondensator und Spule verhält sich nur der reale Widerstand im Wechselstromkreis ebenso wie im Gleichstromkreis. Abweichungen sind erst im sehr hohen Frequenzbereich zu beachten. Durch den Wirkwiderstand fließt zeitgleich ein zur Spannung proportionaler Strom. Der konstante Widerstandswert wird nach dem Ohmschen Gesetz errechnet. Unabhängig vom zeitlichen Verlauf der Spannung am Widerstand ist das Produkt aus Spannung und Strom immer positiv. Am Wirkwiderstand wird zu jedem Zeitpunkt die gleiche Leistung umgesetzt. Er wird warm und bei einer Glühlampe wird zusätzlich Lichtenergie erzeugt. Abweichendes Verhalten ist beim induktiven Blindwiderstand und beim kapazitiven Blindwiderstand zu beobachten, die nachfolgend näher beschrieben werden.
Am Wirkwiderstand gibt es zwischen Strom und Spannung keine Phasenverschiebung.
Am Wirkwiderstand wird kontinuierlich Leistung umgesetzt.
Wirkwiderstände verhalten sich im Gleich- und Wechselstromkreis identisch.
Blindwiderstände
Wird eine Spule, ein induktiver Widerstand im Gleichstromkreis betrieben, so fließt nach dem Schließen des Stromkreises erst nach einiger Zeit ein konstanter Strom. Bis sich dieser Fall, auch eingeschwungener Zustand genannt, eingestellt hat, nimmt der Strom nach einer e-Funktion zu. Im Kapitel: Die Spule im Gleichstromkreis wird dieser Vorgang ausführlich beschrieben. An Gleichspannung betrieben fließt erst nach einer bestimmten Zeit durch die Spule der maximale Gleichstrom, der vom Wirkwiderstand des Spulendrahts bestimmt wird. Bis zum Erreichen des Endzustands nimmt die Spannung parallel zur Spule ab und hat dann ihren vom Drahtwiderstand abhängigen kleinsten Endwert. An diesem Wirkwiderstand wird Verlustleistung umgesetzt. Ganz anders verhält sich die Spule an Wechselspannung.
Die Spule im Wechselstromkreis – Induktiver Blindwiderstand
Zur grundlegenden Betrachtung soll der Draht-(Verlust)-Widerstand der Spule vernachlässigbar klein sein. An diese ideale Spule mit der Induktivität L wird eine sinusförmige Wechselspannung gelegt. Die AC-Sinusquelle soll sich ebenfalls ideal verhalten und keinen Innenwiderstand haben. Es zeigt sich, dass durch die Spule ein sinusförmiger Wechselstrom fließt. Der sich periodisch ändernde Stromfluss erzeugt um die Spule herum ein sich ebenfalls periodisch wechselndes Magnetfeld. Das dynamische Magnetfeld generiert ein sich damit änderndes elektrisches Feld. An den Spulenanschlüssen entsteht eine Spannung, die der angelegten AC-Quellenspannung entgegengerichtet ist. Die parallel zur Spule messbare Spannung wird induktiver Spannungsfall genannt und ist proportional zur Änderungsgeschwindigkeit des Stroms im Stromkreis. Eine vom Strom durchflossene Spule reagiert nach der Lenzschen Regel so, dass sie der sich ändernden Ursache entgegenwirkt. Nur so ist der Energieerhaltungssatz erfüllt, da Energie weder erzeugt noch vernichtet, sondern nur in andere Energien umgewandelt werden kann.
Beim sinusförmigen Strom ist im Nulldurchgang die Steigung der Stromkurve und somit die Änderungsgeschwindigkeit am größten. Mathematisch ergibt sich die Spannungskurve aus der ersten Ableitung der Stromfunktion nach der Zeit. Das Ergebnis ist im Liniendiagramm dargestellt und zeigt, dass zwischen Strom und Spannung an der idealen Spule der Phasenwinkel φ = 90° beträgt. Wird die Spule nach dem Verbraucher-Zählpfeilsystem betrachtet, dann eilt die Spannung dem Strom um 90° voraus oder der Strom läuft um diesen Winkel nach. Merksatz: Bei Induktivitäten die Ströme sich verspäten.
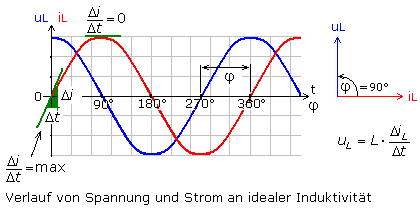
Das Ohmsche Gesetz ist allgemeingültig. Für die Spule kann daher mit Spannungs- und Strommesswerten ein Widerstandswert errechnet werden. Der Quotienten aus der Effektivspannung parallel zur Spule und dem durch sie fließenden Effektivstrom ergibt den Wert ihres Wechselstromwiderstands. Er ist größer als der reale Wirkwiderstand oder Gleichstromwiderstand der Spule. Mit einem Ohmmeter kann nur der Wert des Wirkwiderstands nicht aber der des Wechselstromwiderstands gemessen werden.
In einem Simulationsprogramm wurden drei ideale Spulen unterschiedlicher Induktivität L an einen Sinusgenerator angeschlossen. Die Spannung betrug konstant 10 Veff. Für verschiedene Frequenzen f wurde der sich einstellende Strom ieff gemessen. Die Tabelle zeigt die ermittelten Ergebnisse.
| Induktivität L | 50 mH | 100 mH | 200 mH | |||
| f / Hz | ieff / mA | ueff / ieff in Ω | ieff / mA | ueff / ieff in Ω | ieff / mA | ueff / ieff in Ω |
| 100 | 318,3 | 31,4 | 159,2 | 62,8 | 79,6 | 125,6 |
| 200 | 159,2 | 62,8 | 79,6 | 125,6 | 39,8 | 251,3 |
| 400 | 79,6 | 125,6 | 39,8 | 251,3 | 19,9 | 502,5 |
| 800 | 39,8 | 251,3 | 19,9 | 502,5 | 9,95 | 1005 |
| 1600 | 19,9 | 502,5 | 9,94 | 1006 | 4,97 | 2012 |
| 3200 | 9,91 | 1009 | 4,96 | 2016 | 2,48 | 4032 |
Reale Widerstände verhalten sich im Gleich- und Wechselstromkreis identisch und sind nicht von der Frequenz abhängig. Bei den Spulen zeigt die Auswertung, dass für jede Induktivität eine direkte Proportionalität zwischen der Frequenz und dem Widerstandswert besteht. Eine Spule hat bei doppelter Frequenz den doppelten Widerstandswert. Wird bei konstanter Frequenz der Induktivitätswert verdoppelt, so ist auch der Widerstandswert doppelt so groß. Zwischen Induktivität und Widerstandswert besteht die gleiche direkte Proportionalität. \[\frac{{{u_{eff}}}}{{{i_{eff}}}} \propto f\quad \quad \frac{{{u_{eff}}}}{{{i_{eff}}}} \propto L\quad \Rightarrow \quad \frac{{{u_{eff}}}}{{{i_{eff}}}} \propto f \cdot L\] Aus einer Proportionalität wird durch Multiplikation mit einem Proportionalitätsfaktor k eine Gleichung. Aus den Messwerten kann ein mittlerer Proportionalitätsfaktor errechnet werden: \[k = \frac{{{u_{eff}}}}{{{i_{eff}}}} \cdot \frac{1}{{f \cdot L}} \approx 6,283\] Der Widerstandswert wird induktiver Blindwiderstand genannt und erhält das Formelzeichen XL und die Benennung Ω für Ohm. Sein Kehrwert ist der induktive Blindleitwert mit dem Formelzeichen BL und der Benennung S für Siemens. \[\frac{{{u_{eff}}}}{{{i_{eff}}}} = {X_L} = 2\,\pi \,f\,L = \omega \,L\quad \quad \frac{1}{{{X_L}}} = {B_L} = \frac{1}{{2\,\pi \,f\,L}} = \frac{1}{{\omega \,L}}\] Der genaue Wert des aus der Tabelle ermittelten Proportionalitätsfaktors ist \(k = 2 \cdot \pi \approx 6,2832...\). Exakt gelten die Gleichungen nur für kernlose Spulen (Luftspulen) und für sinusförmige Spannungen und Ströme.
Induktive Blindleistung
Das Liniendiagramm zeigt, dass zwischen Strom und Spannung der Phasenwinkel φ = 90° beträgt. Wird zu jedem Zeitpunkt das Produkt aus Strom und Spannung gebildet, so ist das Ergebnis eine zu null symmetrische sinusförmige Leistungskurve. In jeder Periode pendelt die Energie zwischen der AC-Quelle und der Induktivität zweimal hin und her. Eine ideale Spule gibt im zeitlichen Mittel keine Leistung ab. Das Produkt aus Spannung und Strom wird induktive Blindleistung genannt und hat das Formelzeichen QL mit der Maßeinheit var = V·A. Das Var steht für Volt Ampère réactif und ist die in der Elektrotechnik gesetzliche Einheit der Blindleistung. Im Kapitel Wechselstromleistung gibt es dazu weitere Informationen.
Am idealen induktiven Blindwiderstand eilt bei einem sinusförmigen Strom die Spannung um 90° vor.
Der induktive Blindwiderstand ist direkt proportional zur Frequenz und zur Induktivität.
An einer idealen Spule entsteht keine Wirkleistung.
Die induktive Blindleistung pendelt verlustfrei zwischen Generator und Spule.
Der Kondensator im Gleichstromkreis
Wird ein Kondensator, ein kapazitiver Widerstand im Gleichstromkreis betrieben, so fließt nach dem Einschalten ein Strom, der nach einer e-Funktion abnimmt. Im eingeschwungenen Zustand ist der Kondensator auf die Gleichspannung aufgeladenen und praktisch ist kein Stromfluss mehr messbar. Ausführlichere Informationen liefert das Kapitel: Der Kondensator im Gleichstromkreis. An Gleichspannung betrieben verhält sich ein Kondensator wie eine Unterbrechung mit extrem hohem Widerstandswert. Im Wechselstromkreis verhält sich der Kondensator anders.
Der Kondensator im Wechselstromkreis – Kapazitiver Blindwiderstand
Bei einem theoretisch idealen Kondensator hat das Dielektrikum zwischen den Elektroden einen unendlich großen Isolationswiderstand und die Verbindungen zu den Außenanschlüssen haben keinen Drahtwiderstand. Ist dieser Kondensator mit einem Sinusgenerator einstellbarer Frequenz verbunden, dann ist im Stromkreis ein dauerhafter Wechselstrom messbar, obwohl es keine elektrisch leitende Verbindung über oder durch das Dielektrikum gibt. Die Elektronen fließen auch nicht durch den Kondensator. Sie pendeln zwischen der AC-Quelle und den Elektroden des Kondensators hin und her. Zwischen den Elektroden gibt es einen sogenannten Verschiebestrom, sodass der Kondensator periodisch geladen und entladen oder stetig umgeladen werden kann.
Die Lade- oder Entladestromstärke ist proportional zur Änderungsgeschwindigkeit der sinusförmigen Spannung. Im Liniendiagramm ist zu erkennen, dass sie im Nulldurchgang die größte Steilheit und somit größte Änderungsgeschwindigkeit hat. Zu diesem Zeitpunkt hat die Stromkurve ihren Maximalwert. Die Spannungskurve hat im Maximum den Steigungswinkel null, folglich hat die Stromkurve im Liniendiagramm dort den Wert null. Mathematisch betrachtet ist die Stromkurve das Ergebnis der ersten Ableitung der Spannungsfunktion nach der Zeit. Der ideale Kondensator hat zwischen Strom und Spannung einen Phasenwinkel von 90°, wobei der Strom der Spannung vorauseilt oder die Spannung um diesen Winkelbetrag nachläuft. Merksatz: Beim Kondensator, der Strom eilt vor.
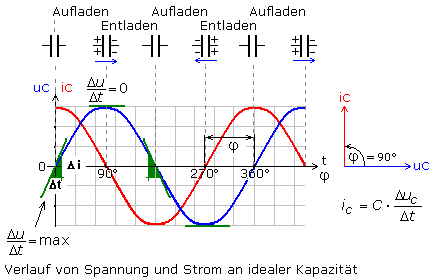
In einem Simulationsprogramm wurden drei ideale Kondensatoren unterschiedlicher Kapazität C an einen Sinusgenerator angeschlossen. Die Spannung betrug konstant 10 Veff. Für verschiedene Frequenzen f wurde der sich einstellende Strom ieff gemessen. Aus den Effektivwerten kann nach dem Ohmschen Gesetz der kapazitive Blindwiderstand berechnet werden. Auch er ist mit einem Ohmmeter nicht messbar. Die Tabelle zeigt die ermittelten Ergebnisse.
| Kapazität C | 50 nF | 100 nF | 200 nF | |||
| f / Hz | ieff / mA | ueff / ieff in kΩ | ieff / mA | ueff / ieff in kΩ | ieff / mA | ueff / ieff in kΩ |
| 100 | 0,314 | 31,85 | 0,628 | 15,92 | 1,257 | 7,96 |
| 200 | 0,628 | 15,92 | 1,257 | 7,96 | 2,513 | 3,98 |
| 400 | 1,257 | 7,96 | 2,513 | 3,98 | 5,027 | 1,99 |
| 800 | 2,514 | 3,98 | 5,028 | 1,99 | 10,055 | 0,99 |
| 1600 | 5,031 | 1,99 | 10,062 | 0,99 | 20,123 | 0,49 |
| 3200 | 10,09 | 0,99 | 20,174 | 0,49 | 40,348 | 0,25 |
Die Auswertung der Tabelle zeigt, dass sich bei einer Frequenzverdopplung der Widerstandswert halbiert. Wird bei konstanter Frequenz der Kapazitätswert verdoppelt, so halbiert sich auch hier der Widerstandswert. Beides entspricht einer umgekehrten Proportionalität. \[\frac{{{u_{eff}}}}{{{i_{eff}}}} \propto \frac{1}{f}\quad \quad \frac{{{u_{eff}}}}{{{i_{eff}}}} \propto \frac{1}{C}\quad \Rightarrow \quad \frac{{{u_{eff}}}}{{{i_{eff}}}} \propto \frac{1}{f} \cdot \frac{1}{C}\] Aus den Messwerten kann ein mittlerer Proportionalitätsfaktor errechnet werden: \[k = \frac{{{u_{eff}}}}{{{i_{eff}}}} \cdot f \cdot L \approx 0,159\] Der Widerstandswert ist der kapazitive Blindwiderstand mit dem Formelzeichen XC und der Benennung Ω für Ohm. Sein Kehrwert ist der kapazitive Blindleitwert mit dem Formelzeichen BC und der Benennung S für Siemens. \[\frac{{{u_{eff}}}}{{{i_{eff}}}} = {X_C} = \frac{1}{{2\,\pi \,f\,C}} = \frac{1}{{\omega \,C}}\quad \quad \frac{1}{{{X_C}}} = {B_C} = 2\,\pi \,f\,C = \omega \,C\] Der genaue Wert des aus der Tabelle ermittelten Proportionalitätsfaktors ist: \(k = 1/2 \cdot \pi \approx 0,1592...\). Die Gleichungen für XC und BC gelten nur bei sinusförmigen Signalgrößen.
Kapazitive Blindleistung
Das Liniendiagramm zeigt, dass zwischen Strom und Spannung der Phasenwinkel φ = 90° beträgt. Wird zu jedem Zeitpunkt das Produkt aus Strom und Spannung gebildet, so ist das Ergebnis eine zu null symmetrische sinusförmige Leistungskurve. In jeder Periode pendelt die Energie zwischen der AC-Quelle und dem Kondensator zweimal hin und her. Im zeitlichen Mittel gibt der ideale Kondensator keine Leistung ab. Die kapazitive Blindleistung hat das Formelzeichen QC und die Maßeinheit var = V·A reaktiv. Var ist die in der Elektrotechnik gesetzliche Einheit der Blindleistung. Im Kapitel Wechselstromleistung gibt es dazu weitere Informationen.
Am idealen kapazitiven Blindwiderstand eilt bei sinusförmiger Spannung der Strom um 90° vor.
Der kapazitive Blindwiderstand ist umgekehrt proportional zur Frequenz und zur Kapazität.
Am idealen Kondensator entsteht keine Wirkleistung.
Die kapazitive Blindleistung pendelt verlustfrei zwischen Generator und Kondensator.