Ersatzspannungsquelle – Thévenin-Äquivalent

Betrachtet werden nur lineare Netzwerke mit unabhängigen Quellen und konstanten Betriebswerten. Oft ist das Verhalten eines Netzwerks für unterschiedliche Belastungen an den Anschlussklemmen von Interesse. Ein lineares Netzwerk mit mehreren Quellen kann in eine äquivalente Spannungsquelle mit ihrem Innenwiderstand umgewandelt werden. Der deutsche Physiker H. von Helmholtz erkannte diese Möglichkeit in der Mitte des 19. Jahrhunderts, die viele Jahre danach vom französischen Telegrafeningenieur L. C. Thévenin neu erkannt wurde.

Die gesuchte Ersatzschaltung wird im deutschen Sprachbereich Ersatzspannungsquelle und international Thévenin-Äquivalent genannt. Sie kann ein Werkzeug zur Analyse und Vereinfachung eines komplizierteren Netzwerks sein. Bei der Umwandlung bleiben die Innenwiderstände der verschiedenen Quellen unverändert. Die äquivalente Spannungsquelle hat einen davon abhängigen anderen Wert für ihren Innenwiderstand. An den Anschlussklemmen ist das Verhalten des Thévenin-Äquivalents identisch mit dem des ursprünglichen Netzwerks.

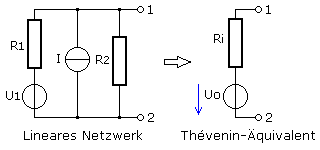
Die Grafik zeigt ein lineares Netzwerk mit einer realen Spannungsquelle und einer realen Stromquelle und den beiden Anschlussklemmen. Die Schaltung rechts stellt die gesuchte Ersatzspannungsquelle mit Innenwiderstand dar, die sich an den Klemmen elektrisch ebenso verhalten soll. Wenig später werden die Leerlaufspannung und der Wert des Innenwiderstands des Thévenin-Äquivalents berechnet.

Videoclip zur belasteten realen Spannungsquelle

Ist der Ausgang einer Spannungsquelle im Leerlauf unbelastet so fließt kein Strom und an ihrem Innenwiderstand entsteht keine Spannung. Die Leerlauf-Klemmenspannung entspricht der idealen Spannungsquelle U0, früher als elektromotorische Kraft (EMK) bezeichnet. Sie kann praktisch durch stromfreies Messen mit einem sehr hochohmigen Spannungsmessgerät (»1 MΩ) zwischen den Klemmen 1 und 2 bestimmt werden.

Der Innenwiderstand könnte theoretisch durch eine Strommessung mit einem geeigneten Amperemeter erfolgen. Es schließt die Spannungsquelle mit seinem sehr kleinen Messwiderstand kurz. Die Klemmenspannung beträgt dann 0 V und die als konstant definierte U0 wäre am Innenwiderstand messbar. Aus der Leerlaufspannung und dem Kurzschlussstrom könnte mithilfe des ohmschen Gesetzes der Wert des Innenwiderstands berechnet werden. Diese Praxis verbietet sich, denn sie kann der Quelle und dem Netzwerk dauerhaften Schaden zufügen.

Eine sichere und bessere Methode ist es, die Klemmen so zu belasten, dass die Ausgangsspannung einen gut messbaren kleineren Wert annimmt. Der Lastwiderstand bildet mit dem zu bestimmenden Innenwiderstand eine Reihenschaltung. Die Leerlaufspannung Spannung U0 teilt sich proportional zu den Widerstandswerten der Reihenschaltung auf. Der Innenwiderstand ist durch einfache Rechnung bestimmbar. Mit den Messwerten aus dem Videoclip kann dieses Verfahren nachvollzogen werden.

Bestimmung des Innenwiderstands bei Leistungsanpassung

Eine Spannungsquelle mit nicht zu kleinem Innenwiderstandswert wird an den Klemmen mit ohmschen Widerständen so lange belastet, bis die Klemmenspannung den halben Wert der Leerlaufspannung hat. Der Wert des Innenwiderstands entspricht ohne Rechnung dem Wert des Lastwiderstands, da sich die Spannung an beiden Widerständen zu gleichen Teilen aufteilt. Dieser Betriebsfall entspricht der Leistungsanpassung, bei der die Quelle ihre maximale Leistung abgibt.

Berechnung der Betriebswerte der Ersatzspannungsquelle

Die Quellenspannung U1 ist konstant. Zur Berechnung des Thévenin-Äquivalents werden im Netzwerk vorhandene Spannungsquellen durch einen Kurzschluss ersetzt. Ihre zugehörigen Innenwiderstände bleiben bestehen. Jeder Quellenstrom Uo ist konstant. Der realen Stromquelle ist ein parallel liegender Innenwiderstand zugeordnet. Zur Berechnung der Ersatzspannungsquelle werden die im Netzwerk vorhandenen Quellen deaktiviert. Die Quellenspannungen werden kurzgeschlossen, die Stromquellen entfernt (Unterbrochen). Ihre Innenwiderstände bleiben unverändert in der Schaltung bestehen. Im Beispielnetzwerk liegen die Innenwiderstände in Blickrichtung auf die Ausgangsklemmen parallel.

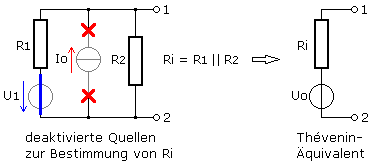
Der Wert des Parallelwiderstands entspricht dem Innenwiderstand des Thévenin-Äquivalents: \[{R_i} = \frac{{{R_1}\,{R_2}}}{{{R_1} + {R_2}}}\quad (1)\] Die Quellen werden aktiviert und die Ausgangsklemmen werden kurzgeschlossen. Zur Berechnung des Kurzschlussstroms zwischen den Klemmen 1 und 2 sind die Erzeugerpfeilrichtungen zu beachten. Der Innenwiderstand der realen Stromquelle R2 ist durch den Kurzschluss unwirksam: \[{I_k} = \frac{{{U_1}}}{{{R_1}}} + {I_o}\quad (2)\] Mit den berechneten Werten für Ri und Ik wird die Quellenspannung Uo des gesuchten Thévenin-Äquivalents berechnet: \[{U_o} = {R_i} \cdot {I_k}\]

In der Beispielschaltung soll die Quellenspannung den Wert U1 = 10 V und den Innenwiderstand R1 = 10 Ω haben. Die Stromquelle soll den Innenwiderstand R2 = 50 Ω haben und Io = 0,5 A abgeben. Nach Gl.(1) errechnet sich der Innenwiderstand der Ersatzspannungsquelle zu Ri = 8,333 Ω. Der Kurzschlussstrom nach Gl.(2) beträgt Ik = 1,5 A. Das ursprüngliche Netzwerk hat am Ausgang die unveränderten Eigenschaften, wenn es durch ein Thévenin-Äquivalent der Quellenspannung Uo = 12,5 V und den Innenwiderstand Ri = 8,333 Ω ersetzt wird. Eine Schaltungssimulation bestätigt alle errechneten Werte.