Realer Einphasentransformator

Im Gegensatz zum idealen Transformator gibt es beim realen Trafo bei der Energieübertragung verschiedene Verluste. Ein Teil der magnetischen Feldlinien wird nicht vollständig im ferromagnetischen Kern konzentriert durch beide Trafowicklungen geführt, sondern streut in den Außenbereich. Für Transformatoren der Energietechnik ist der Koppelfaktor nur nahe eins und kleiner 100%. Das gilt auch für Übertrager mit Magnetkern ohne Luftspalt die in der Nachrichtentechnik verwendet werden.

In der Elektronik werden auch in- oder zueinander verstellbare Luftspulen oder Spulensätze mit einem Ferritkern verwendet, der mehr oder weniger weit in den Spulensatz hineinreicht. Der gewünschte Koppelfaktor wird mithilfe der Justierung erreicht. Bei bekanntem Windungsverhältnis kann durch Division der an den Spulen gemessenen Spannungen der aktuelle Koppelfaktor einfach berechnet werden.

Transformator als Zweitor

Das Ersatzschaltbild eines realen Transformators wird als vereinfachter Zweitor (Vierpol) dargestellt. Links liegt die Eingangsspannung an generiert rechts die Ausgangsspannung. Beide Trafospulen sollen den gleichen Wickelsinn haben und sich auf dem gleichen Kernschenkel befinden. Die angelegte primäre Wechselspannung lässt Strom durch die Primärspule fließen. Sie hat einen ohmschen Drahtwiderstand RCu1. Die Spule erzeugt ein Magnetfeld, das aber nicht vollständig im ferromagnetischen Eisenkern konzentriert wird. Ein geringer Teil der magnetischen Feldlinien verläuft außerhalb des Kerns. Dieser Streufluss wird einer Streuinduktivität XS1 zugeordnet. Er wird von der zweiten Spule nicht erfasst und trägt nichts zur Energieübertragung bei. Das magnetische Hauptfeld wird von der Hauptinduktivität XH erzeugt und ist für die Energieübertragung verantwortlich.

Der Kernwerkstoff ist elektrisch leitend und der wechselnde magnetische Fluss generiert im Kern Wirbelströme. Durch das periodische Ummagnetisieren treten zusätzlich Hysterese-Verluste auf. Beide werden einem ohmschen Widerstand RFe zugeordnet, dessen Leistung als Wärmeenergie freisetzt den Kern erwärmt. Der Drahtwiderstand und die Streuinduktivität liegen in Reihe mit der Parallelschaltung aus Hauptinduktivität und dem definierten ohmschen Kernwiderstand. Mit diesen Komponenten ist der Primärstromkreis geschlossen.

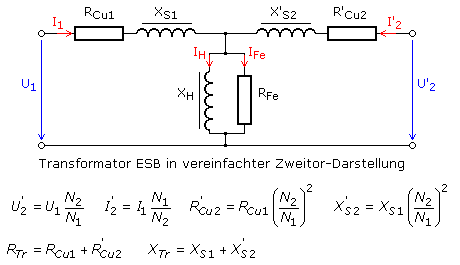
Für die Sekundärseite können die entsprechenden Betrachtungen durchgeführt werden. Im vereinfachten Ersatzschaltbild (ESB) folgt direkt verbunden die Reihenschaltung aus sekundärer Streuinduktivität X'S2 und dem ohmschen Drahtwiderstand R'Cu2 der Sekundärwicklung. Im Normalfall besteht keine galvanische Verbindung zwischen der Primär- und Sekundärseite. Die Größen der Sekundärseite müssen daher auf die Primärseite umgerechnet werden und erscheinen im ESB als gestrichene Größen. Die Umrechnung erfolgt mithilfe des Windungsverhältnisses, dem Übertragungsfaktor des idealen Trafos. Mit dieser Vereinfachung werden primäre und sekundäre Verluste gleich gesetzt und zu einem Gesamtverlust RTr und XTr addiert.

Belastungsabhängiges Verhalten

Leerlaufverhalten

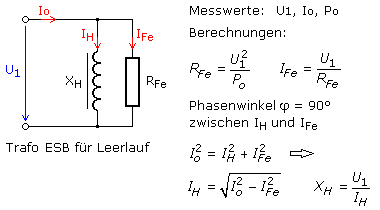
Beim Leerlauf ist der Trafo sekundär nicht belastet und es fließt kein Strom I'2. Der Spulendrahtwiderstand R'Cu2 und die sekundäre Streuinduktivität X'S2 sind unwirksam und kommen im neuen ESB für den Leerlauf nicht vor. Die Hauptinduktivität ist sehr viel größer als die primäre Streuinduktivität, die folglich innerhalb der Messgenauigkeiten vernachlässigt werden kann. Der Kernwiderstand RFe ist im Vergleich zum Spulendrahtwiderstand sehr viel größer. Der primäre Leerlaufstrom wird sich beim Vernachlässigen des Drahtwiderstands innerhalb der Messgenauigkeit nicht ändern. Die Messgröße Po ist eine Wirkleistung, die entweder mit einem passenden Wirkleistungsmessgerät ermittelt wird oder rechnerisch aus der aufgenommenen Scheinleistung und der Phasenverschiebung zwischen Strom und Spannung bestimmt werden muss. Das folgende Bild zeigt das vereinfachte ESB des Trafos im Leerlauf.

Kurzschlussverhalten

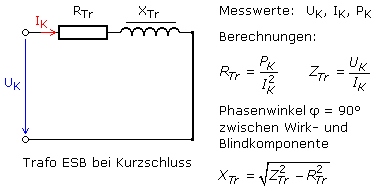
Zur experimentellen Bestimmung der Messwerte darf die Sekundärseite nicht kurzgeschlossen werden, wenn primär die Nennspannung anliegt. Der Primärstrom wird solange erhöht, bis im Sekundärkreis der Nennstrom fließt, der gleich dem Wert des primären Kurzschlussstroms ist. Die Messwerte sind dann die anliegende primäre Kurzschlussspannung UK, der in den Trafo fließende Kurzschlussstrom IK und der Kurzschlussverlust PK als Wirkleistungskomponente.

Beide Wirkwiderstände und beide Streuverluste der Spulen sind wirksam. In diesem Modell werden sie vereinfacht in den gemeinsamen Ersatzgrößen RTr und XTr additiv zusammengefasst. Der primäre Strom I1 und der auf die Primärseite bezogene Strom I'2 sind im Vergleich zum Magnetisierungsstrom IH sehr viel größer. Da die beim Kurzschlussversuch anliegende Primärspannung sehr klein ist, ist der Einfluss von XH und RFe vernachlässigbar gering. Der Querzweig kann im ESB für den Kurzschlussversuch wegfallen. Das folgende Bild zeigt das vereinfachte ESB mit Mess- und Rechenwerten.

Ausführlicheres ESB des realen Transformators

Fließt ein sich zeitlich ändernder elektrischer Strom durch magnetisch gekoppelte Spulen, so wird in der Erreger- oder Primärspule eine Selbstinduktionsspannung und in der Gegen- oder Sekundärspule eine entsprechende Fremdinduktionsspannung erzeugt. Beide Spulen beeinflussen sich gegenseitig. Wird die Sekundärspule kurzgeschlossen, dann sollten sich beim idealen Übertrager die Magnetflüsse im Kern gegeneinander aufheben. Im Realfall verbleiben Kurzschluss-Induktivitäten, die im Zusammenhang mit dem jeweiligen Streufluss stehen. Zur mathematischen Berechnung wird für jede Seite eine Gegeninduktivität M definiert, mit der vom einen auf den anderen Stromkreis umgerechnet werden kann. Der magnetische Fluss Φ wird vom Erregerstrom I, der Windungszahl N und dem magnetischen Widerstand des Kernwerkstoffs Rm bestimmt.

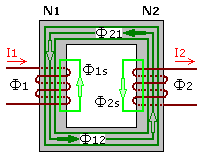
Die folgenden Beschreibungen gelten gleichermaßen für die Primär- und Sekundärseite der durch den magnetischen Fluss gekoppelten Spulen. Die Formeln unterscheiden sich nur in der Indizierung. Im ersten Ansatz ist der Sekundärstromkreis offen und nur die Primärspule wird vom Strom durchflossen. Sie erzeugt den magnetischen Fluss Φ1. Die Sekundärspule erfasst nur einen Teil davon, der als primärer Hauptfluss Φ12 bezeichnet wird. Der geringere primäre Streufluss Φ1s hat sekundärseitig keinen Einfluss. Für die Magnetflüsse wird ein Koppelfaktor k mit 0 ≤ k < 1 definiert. Der magnetische Fluss und die Induktivität stehen in einer mathematischen Beziehung. Die Leerlaufinduktivität kann als Summe einer Hauptinduktivität L1h und Streuinduktivität L1s geschrieben werden.

Die magnetischen Hauptflüsse Φ12 und Φ21 stellen mit dem Koppelfaktor k einen Teil des Gesamtmagnetflusses dar. Gleiches gilt für die Streuflüsse Φ1s und Φ2s, die mit Streufaktoren als Teil des Gesamtflusses geschrieben werden. Für den Streufaktor σ gilt 0 ≤ σ ≤ 1. Die von der Gegenseite nicht erfassten Feldlinien bilden die magnetische Streuung. Sie verringert die Energieübertragung, sodass beispielsweise die induzierte Spannung kleiner bleibt. Es ist ersichtlich, dass die Summe von Koppelfaktor und Streufaktor 1 ergibt. Bei maximaler Kopplung ist die Streuung null und bei maximaler Streuung wird keine Energie übertragen und die Kopplung ist null.

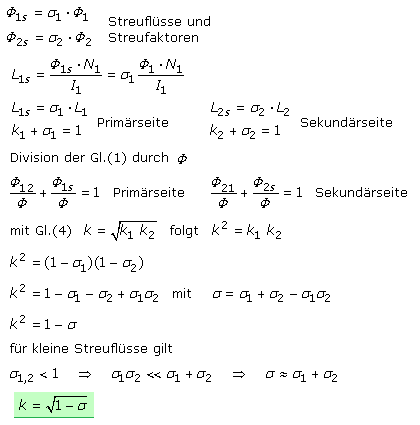
Um vom idealen Transformator (im Bild rechts) zum realen Modell zu kommen, wird gedanklich jede Wicklung um eine in Reihe geschaltete Spule erweitert. Sie wird als Streuinduktivität bezeichnet und die Verluste werden ihrem Blindwiderstand zugerechnet. Die parallel zum Eingang liegende Hauptinduktivität L1h verursacht den Magnetisierungsstrom im Leerlauf und ist im Lastfall gleich der Gegeninduktivität M. Weitere Verluste des realen Transformators ergeben sich aus den ohmschen Widerständen der Wicklungen. Sie werden als Kupferverluste bezeichnet und liegen unter 5%. Wirbelströme im Kernmaterial sind ebenfalls nicht völlig vermeidbar. Durch das periodische Ummagnetisieren des Kerns entsteht Wärme. Diese Verluste werden als sogenannte Eisenverluste bezeichnet, die zwischen (5 ... 10) % liegen. In einer Ersatzschaltung werden sie durch einen linearen ohmschen Wirkwiderstand dargestellt.

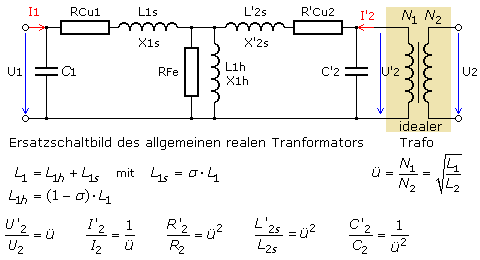
Bei höheren Frequenzen machen sich Wicklungskapazitäten bemerkbar. Bei jedem Trafo lassen sich daher Resonanzfrequenzen messen. Das Übertragungsverhältnis ist von der Frequenz abhängig und verringert sich mit zunehmender Frequenz. Das Ersatzschaltbild des realen Trafos wird den wahren Verhältnissen eines Trafos mit seiner galvanischen Trennung nicht ganz gerecht. Die elektrischen Werte der Sekundärseite sind daher mit ihrem Übersetzungsverhältnis auf die Primärseite umgerechnet (transformiert) worden. Die Trafospulen rechts stehen für den idealen Übertrager mit dem Windungsverhältnis und der galvanischen Trennung.

Die folgende Darstellung zeigt, dass im Leerlauf das reale Übersetzungsverhältnis der Spannungen vom Windungsverhältnis abweicht und etwas größer ist. Das Übersetzungsverhältnis für den Strom ist null, da kein Laststrom fließt. Nimmt die Belastung auf der Sekundärseite zu, dann nehmen die Kupferverluste und die Verluste an den Streuinduktivitäten zu. Das verringert die sekundäre Ausgangsspannung und vergrößert den Übertragungsfaktor der Spannungen.

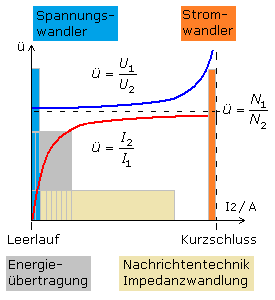
Beim sekundären Kurzschluss mit U2 = 0 V ist der Übertragungsfaktor der Spannung nicht mehr definiert und strebt gegen unendlich. Der Übertragungsfaktor für den Strom erreicht fast den Kehrwert des Windungsverhältnisses. Die unterschiedlichen Arbeitsbereiche, in denen Transformatoren normalerweise eingesetzt werden, sind farbig hinterlegt.

Der Wirkungsgrad η (eta) ist das Verhältnis der abgegebenen Sekundärleistung zur zugeführten Primärleistung. Er wird als prozentualer Wert angegeben, ist bei Nennlast maximal und im Leerlauf geht er gegen null. In Abhängigkeit von der sekundären Belastung bleiben die Eisenverluste in weiten Grenzen konstant.

Die Ausgangsspannung ist von der Art der Belastung abhängig. Die Beispielrechnung zeigt, dass die Spannung am ohmschen, induktiven oder kapazitiven Lastwiderstand mit annähernd gleichem Wert unterschiedlich hoch ist. Der Drahtwiderstandswert der Wicklung soll 10 Ω, der Blindwiderstandswert der Streuinduktivität konstante 50 Ω betragen. Die als ideal angenommene Quellenspannung U20 sei 100 V. Der Lastwiderstandswert soll um 200 Ω liegen. Die Teilwiderstände des Innenwiderstands bilden mit dem äußeren Lastwiderstand eine Reihenschaltung. Der Strom als Bezugsgröße ist in allen Teilwiderständen gleich groß. Mit der Gesamtimpedanz Z ist der Strom errechenbar.

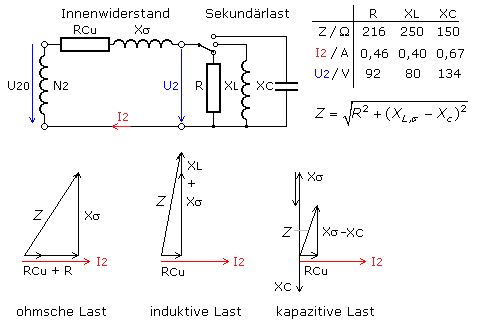
Das Ergebnis zeigt bei induktiver Last eine kleinere Ausgangsspannung U2. Bei kapazitiver Last ist die Spannung größer und kann auch über der Leerlaufspannung liegen. Dieser Fall tritt ein, wenn die Widerstandswerte von XC und Xσ ähnlich sind. Die kapazitive Last bildet mit der Sekundärspule einen Reihenschwingkreis, der im Bereich seiner Resonanz zur Spannungsüberhöhung an diesen Bauteilen führt. Sind die Isolierungen der Wicklungen und des Kondensators dafür nicht ausgelegt, treten Spannungsdurchschläge auf. Bei Resonanzfall erreicht der Strom einen Maximalwert, da er nur noch vom kleinen Drahtwiderstand der Sekundärspule begrenzt wird. Die Wicklung überhitzt sich, die Isolierung kann verbrennen und zum Kurzschluss von Windungen führen.