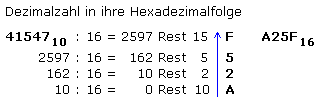Zahlensysteme und Rechnen im Binärsystem
Zahlensysteme haben einen bestimmten Vorrat an Nennwerten aus denen sich alle Zahlen bilden lassen. Zu jedem Nennwert einer einzelnen Ziffer gehört noch ein Stellenwert. Unsere heutigen Zahlensysteme sind Stellenwertsysteme. Das römische Zahlensystem zählt nicht dazu.
Dieses Kapitel befasst sich mit dem Übergang vom Dezimal- zum Dualsystem. Es beschreibt die Addition im Dualsystem und dort auch die Möglichkeit mit negativen Zahlen durch Komplemente zu arbeiten. Für das Dualsystem werden noch Möglichkeiten zur Subtraktion, Multiplikation und Division gezeigt. Zum Ende gibt es einen kurzen Einblick in das Hexadezimalsystem sowie die gegenseitige Umwandlung in das Dezimal- und Dualsystem.
Dezimalsystem
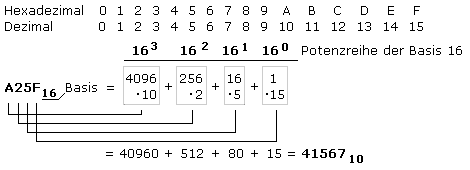
Die Ziffern 0 ... 9 bilden den Nennwertevorrat des Dezimalsystems. Der Nennwert 3 an der ersten oder Einerstelle einer Dezimalzahl steht für den Zahlenwert 3. An der zweiten oder Zehnerstelle steht dieser Nennwert für den Zahlenwert 30. Im Dezimalsystem errechnen sich die Stellenwerte aus der Basis 10 mit dem Stellenwert als Exponenten. Der Zahlenwert errechnet sich aus der Summe aller Teilnennwerte, die mit ihrem jeweiligen Stellenwert zu multiplizieren sind.
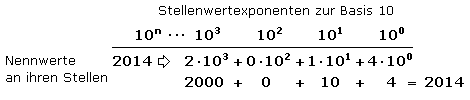
Dualsystem
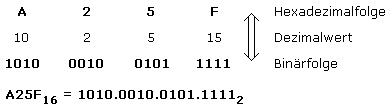
Die elektronische Datenverarbeitung arbeitet fast immer mit digitalen Schaltungen mit den beiden Zuständen EIN oder AUS. Im Binär- oder Dualzahlsystem kommen daher nur die Nennwerte 0 und 1 vor. Die Stellenwerte ergeben sich aus der Basis 2 mit dem Stellenwert als Exponent geschrieben. An jeder Stelle kann der Nennwert 0 oder 1 stehen. Jede Binärzahl lässt sich in ihre Dezimalzahl umrechnen. Dazu wird der binäre Nennwert mit seinem Stellenwert multipliziert und die Summe aller Teilwerte gebildet.

Mit der Indexziffer wird die eindeutige Zuordnung einer Zahl zum verwendeten Zahlensystem angegeben. Im dargestellten Beispiel wird die Dualzahl mit dem Index 2 in ihre Dezimalzahl mit dem Index 10 umgerechnet.
Umwandeln von Ganzzahlen
Die Umrechnung des Dezimalsystems ins Dualsystem ist in der Datenverarbeitung mit elektronischen Binärschaltkreisen von Bedeutung. Als Anwender und Programmierer sind wir eher mit dem Dezimalsystem vertraut. An der Schnittstelle Mensch – Digitalprozessor besorgen automatisch ablaufende Hintergrundprogramme diese Anpassung.
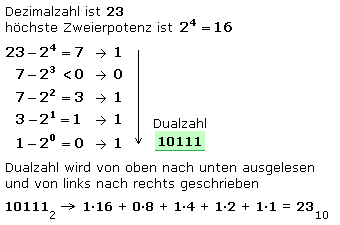
Das Umwandlungsprogramm nach der Subtraktionsmethode zieht von der zu wandelnden Dezimalzahl nacheinander die Zweierpotenzen ab und beginnt mit der größtmöglichen Zweierpotenz. Ist die folgende Zweierpotenz größer als die Differenz der vorherigen Subtraktion, dann wird diesem Stellenwert eine 0 zugewiesen, und die folgende Zweierpotenz abgezogen. Kann die Differenz gebildet werden, so wird diesem Stellenwert eine 1 zugeordnet. Der Vorgang wiederholt sich bis zur niedrigsten Zweierpotenz.
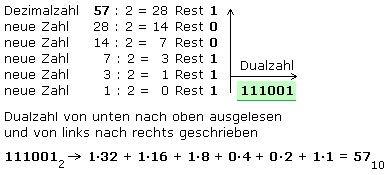
Ein anderes Umwandlungsverfahren entspricht einer wiederholten Ganzzahldivision durch die Basiszahl 2. Mit dem Modulo-2-Verfahren wird die Restzahl, die nur 0 oder 1 sein kann, notiert. Das ganzzahlige Divisionsergebnis ist die neue Zahl. Für die gesuchte Dualzahl werden die Restziffern von unten nach oben ausgelesenen und von links nach rechts notiert.
Umwandeln von Nachkommastellen bei Dezimalzahlen
Die Zweierpotenzreihe der Dualzahlen setzt sich nach dem Komma mit negativen zunehmenden Exponenten fort. Wenn man sie ausrechnet und die letzte Bitstelle der Nachkommareihe als Hauptnenner nimmt, erscheinen im Zähler von links nach rechts abnehmend die gleichen Zweierexponenten wie vor dem Komma.

Dezimale Fließkommazahlen lassen sich ins Dualsystem umrechnen. Die Ganzzahl vor dem Komma wird zum Beispiel mit fortwährender Division durch die Basis 2 und Notieren der Reste gewandelt. Die Nachkommazahl wird mit der Basis 2 multipliziert. Vom Ergebnis wird die Vorkommastelle als Übertrag notiert und die neue Nachkommazahl wieder mit der Basis 2 multipliziert. Beim Schreiben der Dualzahl werden nach der Kommastelle die Überträge von oben nach unten gelesen und von links nach rechts geschrieben. Die Bit-Tiefe der Dualzahl bestimmt das späteste Ende der Umwandlung.
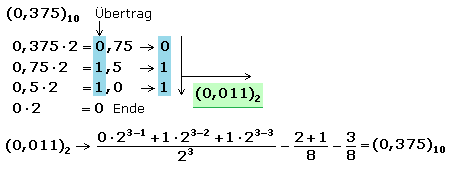
Die Umwandlung dezimaler Nachkommazahlen in die Dualzahl kann auch mithilfe der Subtraktionsmethode erfolgen. Es wird durch die erste negative Zweierpotenz (Divisor) dividiert. Ist die Division bei zu kleinem Dividenden nicht möglich, wird eine 0 notiert und die Division mit der folgenden negativen Zweierpotenz fortgesetzt. Bei erfolgreicher Division wird eine 1 notiert und ein verbleibender Rest vom Dividenden subtrahiert. Die Division wird mit der folgenden niedrigeren Zweierpotenz fortgesetzt. Das Divisionsverfahren endet spätestens beim Erreichen der festgelegten Bit-Tiefe.
 △
△
Rechenregeln für das Dualsystem
Addition im Dualsystem
Dualzahlen werden nach der gleichen Methode wie im Dezimalsystem addiert. Die Zahlen werden untereinander geschrieben und spaltenweise addiert. Im Dualsystem gilt 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1 und 1 + 1 = 0 mit dem Übertrag 1, der an die nächsthöhere Stelle weitergegeben wird.

Überschreitet das Additionsergebnis bei einer festgelegten Bit-Tiefe den Wertebereich der darstellbaren Dualzahlen, so kann der Übertrag an der höchsten Stelle nicht gespeichert werden. Es wird ein falsches Ergebnis angezeigt.
Negative Zahlen im Dualsystem
Eine 4-Bit Dualzahl codiert positive ganze Dezimalzahlen zwischen 0 ... 15. Ist der Darstellbereich auf 4 Bit begrenzt und man addiert 1, gelangt man zu binär 0000, da das 5. Bit als Übertrag nicht angezeigt werden kann. Die 4-Bit Datenworte lassen sich im Zahlenkreis darstellen.
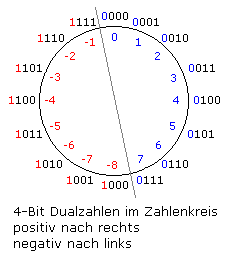
Halbiert man den Kreis so, dass an der höchsten Bitstelle immer eine 0 oder eine 1 steht, dann kann das MSB als Vorzeichenbit definiert werden. In der Menge der ganzen Zahlen ist der Vorgänger von 0 die −1. Die Binärzahl 1111 stellt somit die negative Dezimalzahl −1 dar.
Im Zahlenkreis gibt es ein scheinbares Problem bei dual 1000 für dezimal +8 und −8, da vom MSB per Definition eine negative Zahl gefordert wird. Im 4-Bit Zahlenkreis sind die Dezimalzahlen −8 ... 0 ... +7 binär codiert.
Die dezimale 0 ist der Menge der positiven ganzen Zahlen zugeordnet, sodass der Zahlenkreis 8 positive und 8 negative ganze Zahlen umfasst.
Addiert man zu einer positiven ganzen Zahl ihren negativen Wert, dann ist das Ergebnis 0. Das sollte auch in der Binärdarstellung so sein. Um vom positiven Bitmuster einer Zahl zum negativen Bitmuster der gleichen Zahl zu gelangen, muss man alle Bits invertieren und 1 Bit addieren. Dezimal +5 gleich dual 0101 wird invertiert zu 1010, addiert mit 0001 ergibt dual 1011 und entspricht damit dezimal −5.
Einerkomplement
Das erste Bit eines n-Bit langen Datenworts wird most significant bit, MSB genannt und steht für das Vorzeichenbit. Die folgenden n−1 Stellen codieren den Zahlenwert. Im Einerkomplement sind diese Bitstellen invertiert. Positive Zahlen haben im MSB eine 0, negative Zahlen eine 1. Ist das Datenwort länger als zur Codierung notwendig, werden in der Einerkomplementschreibweise nicht genutzte Stellen bei positiven Zahlen mit vorangestellten Nullen aufgefüllt. Bei negativen Zahlen werden die nicht genutzten Stellen mit führenden Einsen aufgefüllt.
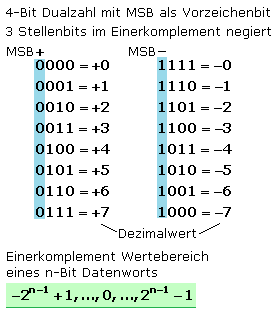
Der Wertebereich einer n-Bit langen Zahl im Dualsystem ist in Anwendung der Einerkomplementdarstellung symmetrisch. Die dezimale 0 hat einen positiven und negativen Binärwert und ist so für einen mathematischen Vergleich oder dem Prüfen auf 0 nicht geeignet. Bei der Addition muss das Ergebnis ≤7 sein, sonst wird vom MSB ein negatives Ergebnis angezeigt. Die Subtraktion im Dualsystem durch Addition der Einerkomplemente liefert nur dann ein korrektes Ergebnis, solange der Übertrag nicht über die höchste Bit-Zahl hinausgeht.
Zweierkomplement
Bei der Codierung negativer Dezimalzahlen wird der absolute Zahlenwert codiert. Alle Bitstellen werden negiert (invertiert) und zum Ergebnis der Wert 1 addiert. Die Inversion ergibt das Einerkomplement, das durch die Addition von binär 1 dann zum Zweierkomplement wird. Das MSB zeigt das Vorzeichen an.

Bei positiven Zahlen steht im MSB eine 0, bei negativen Zahlen eine 1. Der Wert null ist einer positiven Zahl zugeordnet und hat im Zweierkomplement keine Doppeldarstellung mehr. Durch die Addition von binär 1 zum Einerkomplement 1111 entsteht 10000, wobei der Übertrag mit einem 4-Bit Datenwort nicht angezeigt werden kann. Der Wertebereich einer n-Bit langen Zahl im Zweierkomplement ist daher nicht mehr symmetrisch. Der positive Bereich schließt die 0 mit ein und ist um einen Absolutwert kleiner.
Weitere Informationen zum Begriff Komplement kann man mit Beispielen im Bereich der Fachmathematik nachlesen.
Subtraktion im Dualsystem
Im Dualsystem scheinen alle durch 0 und 1 darstellbaren Zahlen immer positiv zu sein. Wird das MSB als Vorzeichenbit definiert, verkleinert sich der codierbare Zahlenbereich eines n-Bit langen Datenworts und man kann positive und negative Zahlen darstellen. Im Dualsystem stellen die Einerkomplemente das gegenteilige Bitmuster einer gegebenen Dualzahl dar. Jedes Bit der Dualzahl ist in seinem Komplement invertiert. Mit der Addition von binär 1 zum Einerkomplement erhält man das Zweierkomplement, mit dem dann die Subtraktion als Addition ausgeführt werden kann.
Wird die Subtraktion auf eine Addition zurückgeführt, ist von der abzuziehenden Zahl, dem Subtrahenden das Komplement zu bilden. Das Komplement einer n-stelligen Zahl ist der Ergänzungswert zur Basis. Im Dezimalsystem ist das Zehnerkomplement von 7 die 3, da 10 − 7 = 3 ist. Soll von dezimal 7 die 7 subtrahiert werden, kann durch Addition des Zehnerkomplements das gleiche Ergebnis wie bei der direkten Subtraktion erhalten werden, da bei einstelliger Darstellung der entstehende Übertrag nicht angezeigt werden kann.
Im Dualsystem ist 2 die Basis, folglich wird anstelle der Subtraktion das Zweierkomplement des Subtrahenden addiert. Ein über die festgelegte Bit-Breite hinausgehender Übertrag wird verworfen und nicht gespeichert. Das Zweierkomplement einer negativen Dualzahl ergibt den Absolutwert der Zahl.

Ist die zu subtrahierende Dualzahl größer als die Zahl, von der sie abgezogen wird, so steht im Ergebnis eine 1 im MSB und es gibt keinen Übertrag an die folgende Exponentialstelle. Das Ergebnis und die entsprechende Dezimalzahl sind negativ. Der Absolutwert kann erst ermittelt werden, wenn von der Dualzahl nochmals das Zweierkomplement gebildet wird.

Multiplikation im Dualsystem
Die Multiplikation ist eine zusammengesetzte Operation aus einer Bit-Verschiebung nach links und der Addition der verschobenen Datenworte. Die Bitbreite bestimmte dabei den darstellbaren Wertebereich muss beachtet werden, da ein Stellenübertrag an der höchsten Stelle nicht ausgewertet werden kann.
In einer einfachen Multiplikation mit Zweierpotenzen ist das Linksshift-Verfahren gut erkennbar. Die zu multiplizierende Dualzahl wird um die Anzahl der Stellen nach links verschoben, an der eine 1 im Multiplikator steht.
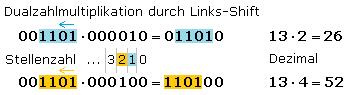
Ist der Multiplikator eine beliebige Dualzahl, muss das Linksshift-Verfahren nacheinander mit jedem Stellenwert, wo eine 1 steht erfolgen. Die Addition der geschobenen Dualzahlen ergibt anschließend das gesuchte Ergebnis der Multiplikation.

Division im Dualsystem
Bei der Division im Dezimalsystem ist das Ergebnis oft eine Zahl mit endlichen oder unendlichen Nachkommastellen und unterscheidet sich so von den anderen Grundrechenarten. Im Dualsystem ist die Division durch Zweierpotenzen als Umkehrung der Multiplikation durch die Rechtsverschiebung der Bitfolge durchführbar. Dieses Rechtsshift-Verfahren ist auf Zweierpotenzen beschränkt. Eine Rundung findet nicht statt. Nach rechts aus dem Bitmuster fallende Stellen werden verworfen.

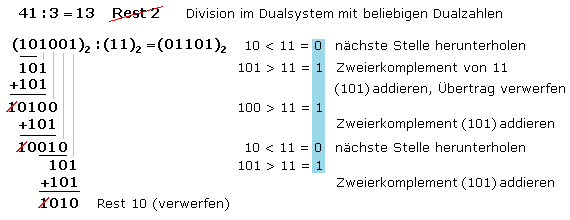
Das Verfahren zur Division durch eine beliebige Dualzahl ist vergleichbar mit der schriftlichen Division im Dezimalsystem. Die Subtraktion der Zwischenergebnisse erfolgt nach dem weiter oben beschriebenen Verfahren mit Zweierkomplementen. Ein bleibender Divisionsrest wird nicht berücksichtigt und wie oben abgeschnitten.
 △
△