Rauschen in der Elektronik
Mit Rauschen verbindet man ein akustisches Signal, dem keine entschlüsselbare Information entnommen werden kann. Treten Informations- und Rauschsignale gemeinsam auf, wird das Rauschen bei zu großer Amplitude als störend empfunden. Die Amplitude eines Rauschsignals bestimmt die Genauigkeit an der unteren Messwertgrenze. Rauschen ist ein stochastisches Signal und entsteht durch statistische Änderungen physikalischer Größen, die deterministisch nicht beschreibbar sind.
Es wird zwischen äußeren und inneren Rauschquellen unterscheiden. Ein im Rundfunkempfang typisches Beispiel äußerer Rauschquellen sind elektrische Störungen durch die veränderliche Luftelektrizität bei gewittriger Wetterlage. Die Störungen liegen im Frequenzbereich bis 10 MHz und sind besonders auf Lang-, Mittel- und Kurzwelle beim Empfang schwacher Sender als Rauschen unterschiedlicher Intensität hörbar. In der Radioastronomie stören die Radiostrahlung ferner Sterne und die diffuse Weltraumstrahlung im Frequenzbereich oberhalb 50 MHz die ohnehin schon sehr schwachen Nutzsignale.
Weißes Rauschen
Eine ständige innere Rauschquelle wird vom thermischen Rauschen bestimmt, das nur am absoluten Nullpunkt der Temperatur bei 0 Kelvin nicht mehr besteht, da sich dann alle Teilchen in Ruhelage befinden. Oberhalb von 0 Kelvin sind im Werkstoff alle Atombausteine und damit auch die Elektronen in einer stetigen unregelmäßigen Bewegung, die mit steigender Temperatur zunimmt. Im Werkstoff entstehen dadurch statistisch verteilt kleinste Ladungsverschiebungen. An den Anschlüssen eines ohmschen Widerstand erzeugen sie in der Summe eine außen messbare thermische Rauschspannung.
Jeder gerichtete Stromfluss im Widerstand oder einem anderen elektronischen Bauteil wird von statistisch unregelmäßigen Bewegungen der Ladungsträger überlagert. Werden mit einem Oszillograph kleine Nutzsignale in hoher Verstärkung gemessen, so ist das Signalbild oftmals nicht optimal scharf darstellbar. Eine Ursache dieser Unschärfe ist das thermische Rauschen der Signalquelle und wird auch vom Messverstärker selbst verursacht. Bei weiterer Verstärkung kann es als akustisches Rauschsignal hörbar gemacht werden.
Thermisches Rauschen
Das thermische oder Widerstandsrauschen, auch als Johnson- oder Nyquist-Rauschen bezeichnet, ist proportional zur Temperatur und zum Widerstandswert. Die Proportionalitätskonstante ist die Boltzmann-Konstante k. Sie gibt an, wie viel mittlere thermische Energie pro Kelvin einem Ladungsträger zugeführt wird. Das thermische Rauschen ist unabhängig von der Frequenz, nimmt aber mit zunehmender Bandbreite zu. Das Rauschen wird oft durch die Leistungsspektraldichte PSD (power spectral density) oder Rauschleistung in der Einheit W / Hz beschrieben. Für alle Berechnungen sind die Effektivwerte zu verwenden.
Stellt man innerhalb eines ausreichend langen Zeitraums die Häufigkeit der Amplitudenwerte der thermischen Rauschspannung grafisch dar, entsteht eine Gaußsche Normalverteilung mit null als Mittelwert. Zum Messen bestimmt man den quadratischen Mittelwert und daraus den Effektivwert. Eine animierte Gaußsche Verteilung und der mathematische Hintergrund sind beim Galtonbrett dargestellt. Das folgende Bild zeigt einen sehr kurzen Ausschnitt eines per Audiosoftware generierten weißen Rauschsignals. Die rechts als Balkendiagramm aufgetragenen Häufigkeiten gleicher Amplitudenwerte entlang der Horizontalen entsprechen einer Gaußschen Verteilung. Der errechnete Mittelwert von −0,3 bei nur 970 Momentanwerten kommt dem Idealwert 0 der mittleren Rauschspannung recht nahe.
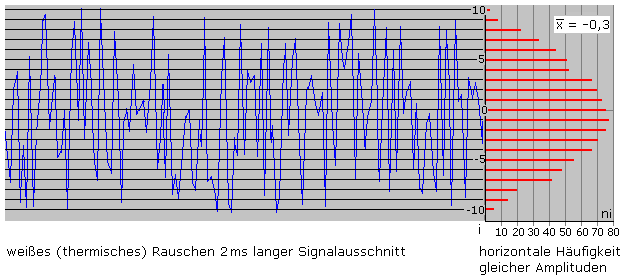
Die mittlere Rauschspannung über einen unendlichen Zeitraum ist der Grenzwert aus der Summe aller Momentanwerte und hat den Wert null als Ergebnis. Gemessen wird der quadratische Mittelwert nach der von Nyquist erstellten Gleichung oder der daraus folgende Effektivwert. Mit dem Effektivwert kann eine vom Widerstandswert unabhängige thermische Rauschleistung berechnet werden.

Die Effektivwerte der Rauschspannung ohmscher Widerstände sind proportional zur Temperatur und Bandbreite. Die Werte sind nicht sehr hoch. So errechnet sich das Eigenrauschen eines 1 MΩ Widerstands bei 25 °C = 298 K und einer Bandbreite von 10 MHz zu Ur = 406 μV.
Das thermische Rauschen oder Johnson-Rauschen wird allgemein als weißes gaußsches Rauschen bezeichnet, da sein Leistungsdichtespektrum in jedem Frequenzbereich konstant ist. Sein Amplituden-Frequenzspektrum zeigt sich in allen Frequenzabschnitten als Band gleicher Intensität. Unserem Hörempfinden nach beurteilen wir weißes Rauschen eher höhenbetont, da unser Gehör mit zunehmender Frequenz logarithmisch empfindlicher reagiert.
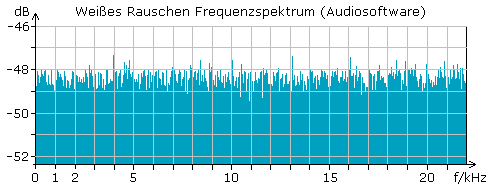
Weißes Rauschen 5 s Tonbeispiel
Schrotrauschen – Schottky-Rauschen
Dem weißen Rauschen wird das Schrotrauschen (englisch: shot noise) zugeordnet. Es wird auch als Schottky- oder Stromrauschen bezeichnet, denn es entsteht zusätzlich zum thermischen Rauschen, wenn Ladungsträger voneinander unabhängig Potenzialbarrieren durchlaufen. Eine am Bauteil angelegte Spannung generiert einen Stromfluss, der aber infolge zu weniger Ladungsträger noch nicht korreliert fließt. Diese Bedingungen sind besonders an den pn-Übergängen der Halbleiter und geheizten Vakuumröhren gegeben. In der Natur ist Schrotrauschen im fallenden Regen hörbar, da sich jeder Tropfen unabhängig von allen anderen bewegt.
In den Sperrschichten der Halbleiter setzt sich der Gesamtstrom aus einem Elektronen- und Defektelektronen- (Löcher)-Strom zusammen und es kommt zu Rekombinationen zwischen Elektronen und Defektelektronen. Das Schrotrauschen wird daher besonders von Dioden- und Sperrströmen bei Transistoren und dem Lawinenstrom (avalanche noise) von Z-Dioden oberhalb 5 V generiert. Ein optimales Schrotrauschen entsteht bei Z-Dioden, wenn Ladungsträger die Energiebarriere vom Valenz- ins Leitungsband durchtunneln. Dieser Effekt tritt oberhalb der 5 V Sperrspannung auf.
Im linearen Kennlinienbereich der Halbleiter errechnet sich das Quadrat des mittleren Rauschstroms aus dem aktuellen Gleichstrom I, den Elementarladungen qe (Elektron und Defektelektron) und der betrachteten Bandbreite. Der Wert ist von der Temperatur und der Frequenz unabhängig, wenn die Messzeiten lang im Vergleich zur Rekombinationszeit der Ladungsträger sind. Werden die Halbleiter im gekrümmten Kennlinienbereich außerhalb der Sättigung betrieben, kommt ein Reduktionsfaktor zwischen 0,2 ... 0,3 hinzu.
Weißes Rauschen wird in der Elektronik und Audiotechnik als Referenzsignal eingesetzt und durch Rauschgeneratoren erzeugt. Besonders hochwertige Generatoren nutzen rein thermische Rauschquellen mit geheizten speziellen Widerständen. Die erreichbaren Signalamplituden liegen im Nano- und Mikrovoltbereich, wobei ein komplexer apparativer Aufwand notwendig ist. Normalerweise werden die pn-Strecken von Dioden, Z-Dioden und Transistoren als Rauschquelle verwendet. Das Signal wird danach auf die Nutzamplitude verstärkt und der Frequenzbereich ausgefiltert. Diese Generatoren erzeugen eine Überlagerung aus thermischen gaußschen Rauschen, dem Schottky-Rauschen und dem Eigenrauschen der Verstärkerstufen.
Rosa-(1/f)-Rauschen
Auch hierbei gibt es weitere Bezeichnungen wie Funkelrauschen, Flickerrauschen und Stromverteilungsrauschen. Das Rauschen verhält sich umgekehrt proportional zur Frequenz und ist bei tiefen Frequenzen bis 10 kHz besonders störend. Im Amplituden-Frequenzspektrum nimmt die Leistungsdichte pro Oktave um 3 dB ab. Das 1/f-Rauschen setzt Stromfluss voraus und tritt beim Anodenstrom von Vakuumelektronenröhren und in Halbleitern auf. Verantwortlich für das 1/f-Rauschen sollen Schwankungen in der Zahl der freien Ladungsträger im Leitungsband von Halbleitern sein.
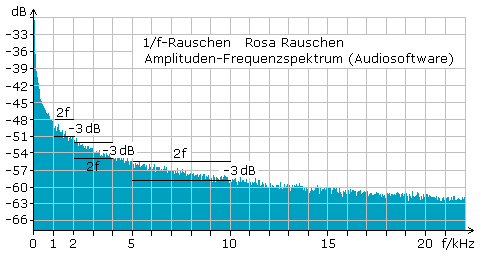
Rosa-Rauschen 5 s Tonbeispiel
Besonders bei MOSFET-Halbleitern werden Haftstellen und Kristallgitterstörungen zwischen dem SiO2-Isolator und dem Si-Kanal verantwortlich gemacht. Dort können Ladungsträger kurzzeitig anhaften und wieder freigegeben werden. Der Effekt ist bei n-Kanal Transistoren größer als bei p-Kanal Transistoren, da die Energiebarriere der Letzteren höher ist. In NF-Verstärkern sollten daher Bipolartransistoren oder JFET verwendet werden. Die im Arbeitspunkt stets vorhandene Raumladungszone verhindert zu hohe Amplituden des 1/f-Rauschens.
Praktisch tritt bei allen elektronischen Bauelementen 1/f-Rauschen auf. Besonders stark ist es bei gepressten Kohlekorn- und Kohleschichtwiderständen, wo es an den Korngrenzen zu statistisch variierenden Leitfähigkeiten mit partiellen Temperaturänderungen kommt. Bei den Bariumoxid-Elektronenemittern indirekt geheizter Elektronenröhren sind es ebenfalls kleine Widerstandsunterschiede im Material. Bei direkt geheizten Wolframkathoden verdampfen immer einige Metallatome und werden ionisiert. Selbst bei metallischen Leitern und besonders an den Kontaktstellen zum Halbleiterkristall verursachen die vorhandenen Gitterstörungen im Werkstoff das Rauschen.
Beim 1/f²-Rauschen, auch rotes oder Brown(sches)-Rauschen genannt, fällt die Leistungsdichte pro Oktave um 6 dB ab. Die mathematische Beschreibung der Brownschen Molekularbewegung liefert ein derartiges Ergebnis. Im Gegensatz zu den Ladungsträgern mit extrem kleiner Masse haben die Modellpartikel, an denen die ungeordneten Bewegungen von Robert Brown beobachtet und beschrieben wurden große Massen. Je schneller sie sich bei zunehmender Frequenz bewegen, desto mehr behindert sie sich gegenseitig und ihr Verhalten ist nicht so ideal unkorreliert wie gefordert.
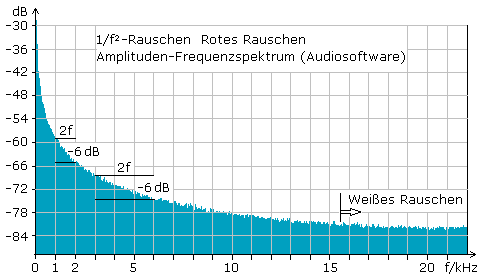
Brown-Rauschen 5 s Tonbeispiel
Ein von J. B. Johnson 1925 im Experiment ermitteltes und 1926 von W. Schottky aus den Messreihen mathematisch beschriebenes und nach der optischen Erscheinung benanntes Funkelrauschen der Elektronenemission aus Glühkathoden zeigte ein 1/f²-Leistungsdichtespektrum. Bei direkt oder indirekt geheizten Elektronenröhren sind es die aus der Kathode unregelmäßig freikommenden Elektronen. Durch Abstoßung untereinander und thermische Unterschiede in der Röhre legen sie unterschiedlich lange Wege zur Anode zurück und bilden so mit statistischen Stromschwankungen den Anodenstrom. Beim Glühen ließ sich auf der Kathodenoberfläche ein geringes Funkeln beobachten.
Das 1/f²-Rauschen geht oberhalb von 15 kHz in das Leistungsdichtespektrum des weißen Rauschens über. Gleiches wird auch beim 1/f-Rauschen ab rund 25 kHz beobachtet. Das Rauschen elektronischer Schaltungen setzt sich stets aus mehreren sich überlagernden Komponenten zusammen, die nur in bestimmten Bandbreiten besonders störend wirksam sind.
Blaues Rauschen
Im Gegensatz zum bisher beschriebenen farbigen Rauschen nimmt beim Blauen Rauschen die Rauschenergie mit 3 dB / Oktave zu und verhält sich umgekehrt zum Rosa Rauschen. Die Energiedichte nimmt proportional zur Frequenz zu und ist auf eine Oktave bezogen konstant.
Phasenrauschen
Das Phasenrauschen entsteht durch unregelmäßige und nicht periodische Änderungen der Phasenlage eines Signals. Eine Oszillatorfrequenz wird durch eine instabile Versorgungsspannung und besonders durch Änderungen der Umgebungstemperatur beeinflusst. Sie wirkt auf die Güte der Bauteile und damit auf die Rückkoppelfaktoren ein. Angegeben wird das Phasenrauschen als Dezibelwert dBC bezogen auf (Carrier) die Träger- oder Oszillatorfrequenz für einen bestimmten Abstand von der Oszillatorfrequenz. Das Phasenrauschen ändert sich mit der gewählten Bandbreite und wird mit größerem Abstand von der Oszillatorfrequenz kleiner.
Rauschgrößen
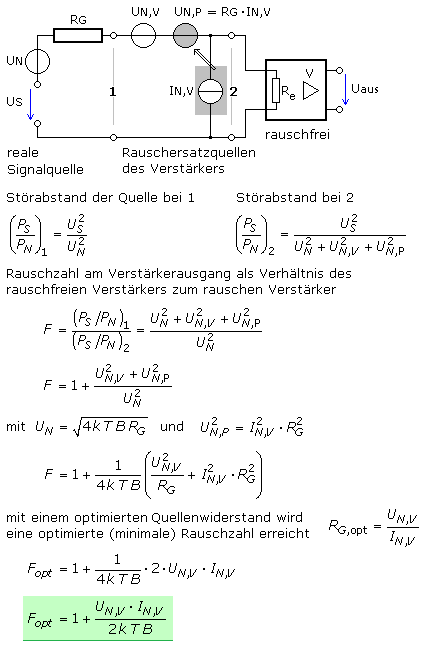
Jede Signalquelle und somit auch jede Verstärkerschaltung hat eine Impedanz, deren ohmscher Komponente das Rauschsignal zugeordnet werden kann. Reine Blindwiderstände tragen nicht zum Rauschen bei. Zur Vereinfachung definiert man den ohmschen Innenwiderstand der Quelle als rauschfrei und erweitert sie um eine Rauschspannungsquelle. Jede Spannungsquelle kann in ihre äquivalente Stromquelle mit parallel geschaltetem rauschfreien ohmschen Widerstand umgerechnet werden.
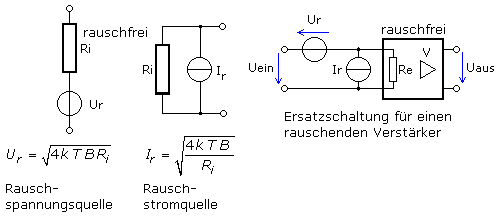
Die Ersatzschaltung eines rauschenden Verstärkers wird mit einer vorgeschalteten Rauschspannungsquelle und einer parallel zum Eingang liegenden Rauschstromquelle selbst zu einem idealen rauschfreien Verstärker mit seiner Eingangsimpedanz. Das Verhalten der beiden Rauschquellen soll vereinfacht gesehen statistisch und voneinander unabhängig (unkorreliert) sein. Bei einem idealisierten Zweitor sind beide Rauschquellen am Eingang notwendig. Bei Leerlauf am Eingang liefert die Rauschstromquelle das Rauschsignal. Fehlt die Rauschspannungsquelle, dann wäre bei Kurzschluss am Eingang auch das Rauschen kurzgeschlossen.
Eine rauschende Signalquelle erzeugt Rauschleistung und überträgt sie an einen angeschlossenen Lastwiderstand. Beide Widerstände werden als rauschfrei definiert. Ist der Quellenwiderstand gleich dem Lastwiderstand, dann wird die maximale Leistung übertragen und für die Rauschleistung PN (N für noise) ergibt sich die folgende einfache Beziehung.

Rauschtemperatur
Mit dieser für Leistungsanpassung hergeleiteten Gleichung kann die Rauschtemperatur angegeben werden, die ein realer ohmscher Widerstand haben müsste, um die Rauschleistung PN zu generieren. Darin ist k·T die spektrale Rauschleistungsdichte. Der Bezugs- oder Vergleichswert wird mit der Temperatur 290 K oder 17°C berechnet.

Störabstand – Signal-Rausch-Verhältnis
Jede elektronische Schaltung kann auf unterschiedliche Weise ein Eigenrauschen generieren. Das Verhältnis von Nutzsignalleistung und Störsignalleistung wird als Störabstand S oder Signal-Rausch-Verhältnis, signal to noise ratio (SNR) bezeichnet. Der Wert wird meistens in dB angegeben, wobei zur Umrechnung ins logarithmische Maß bei Leistungen der Faktor 10 zu verwenden ist. Die Dynamik eines Signals ist maximal so groß wie ihr SNR-Verhältnis, da darüber hinaus der Verstärker mit dem Signal auch das Rauschen verstärkt. Für ein gerade noch verständliches Signal muss das Signalrauschverhältnis ≥2 sein. Ein relativ rauscharmes Signal weist ein Verhältnis von mindestens 20 ... 50 auf. Die Rundfunk Empfangstechnik fordert mit 26 dB ein Störabstand von rund 400.
Durch eine Expandertechnik kann das SNR verbessert werden. Das Nutzsignal wird beispielsweise vor der Übertragung in seinem hohen Frequenzbereich mehr verstärkt. Das durch die Übertragungsstrecke hinzugekommene Rauschen macht sich im hohen Frequenzbereich störender bemerkbar. Die zum Sender gegenläufige Amplitudensenkung stellt den linearen Signalfrequenzgang wieder her und verringert dabei die Rauschamplituden.

Rauschzahl
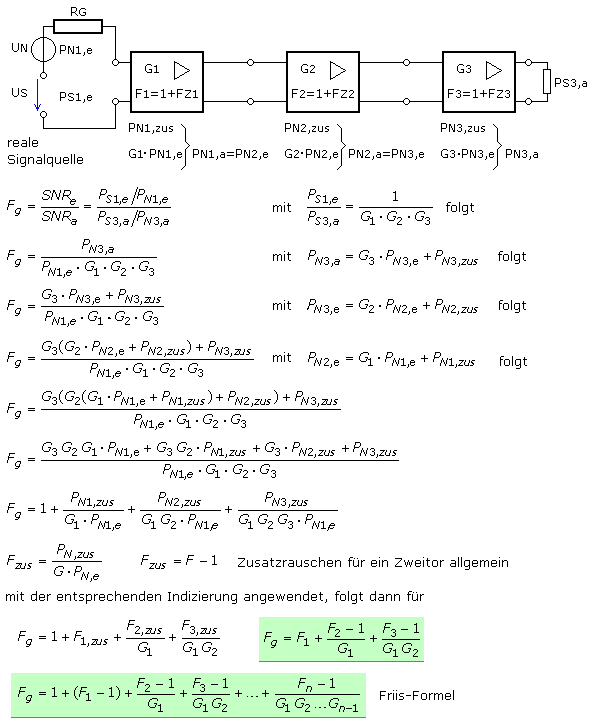
Eine Schaltung verstärkt ein Eingangssignal linear mit dem Faktor G, dem Verhältnis vom Ausgangs- zum Eingangssignal. Jedes Signal ist mit einem Rauschsignal überlagert, das vom Zweitor verstärkt wird und sein eigenes Rauschsignal hinzufügt. Die Rauschzahl F ist das Verhältnis des Störabstands am Eingang eines Zweitors zum Störabstand am Ausgang. Das Rauschmaß ist der dekadische Logarithmus der Rauschzahl in dB.
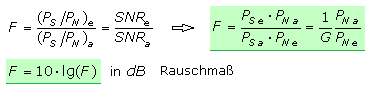
Für die folgenden Betrachtungen soll das Eigenrauschen eines Verstärkers unabhängig (unkorreliert) zum Rauschen des Eingangssignals sein. Zwischen Signalquelle und Zweipol besteht Leistungsanpassung. Die Rauschleistung der Quelle PN,e wird mit G verstärkt und bildet mit dem Eigenrauschen PN,V die Ausgangsrauschleistung PN,a des Zweipols. Definiert man den Zweipol als rauschfrei, so kann sein Eigenrauschen als eine am Eingang wirkende Rauschquelle angenommen werden. Ihre Rauschleistung ist proportional zur effektiven Rauschtemperatur Teff und gelangt mit G verstärkt als PN,V an den Ausgang.
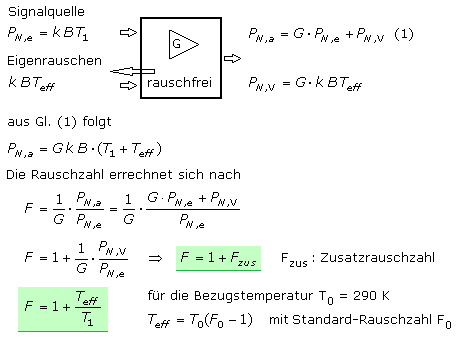
Die Rauschzahl F ist das Verhältnis der Ausgangsrauschleistung eines realen rauschenden Verstärkers zur Ausgangsrauschleistung des idealen Verstärkers. Es ist zu erkennen, dass sich das Eigenrauschen besonders negativ bemerkbar macht, wenn der Nenner G · PN,e klein ist. Das Rauschen der Signalquelle oder ihre entsprechende Rauschtemperatur beeinflussen in jedem Fall die Rauschzahl eines Verstärkers. Je niedriger die Rauschtemperatur der Quelle ist, desto größer ist die Rauschzahl beim gleichen Verstärker. Die Rauschzahl eines idealen Verstärkers ist F = 1, das entsprechende Rauschmaß kann somit nicht kleiner als F = 0 dB sein. Oft wird mit der proportionalen Rauschtemperatur gerechnet. Der Bezugswert ist auf 290 K festgelegt, zu dem F0 die Standard-Rauschzahl ist.