Das Galtonbrett – Normalverteilung nach Gauß
Traue keiner Statistik, die Du nicht selber erstellt hast.
Ein sehr bekannter physikalischer Versuch ist das Galtonbrett. Von oben einfallende Kugeln treffen auf ihren Weg nach unten auf regelmäßig angeordnete Hindernisse, meistens gleichartige Stifte. Dort werden sie entweder nach rechts oder links abgelenkt, um nach kurzer Fallstrecke erneut auf einen Stift zu treffen. Unten angekommen fallen sie in Sammelbehälter, wo ihre Verteilung notiert wird. Abhängig vom idealen Aufbau der Hindernisse und von der Homogenität der Kugeln zeigt sich in vielen Versuchen eine symmetrische, glockenförmige Verteilung.
Der Versuch ist vom Zufall gesteuert. Es ist nicht vorhersagbar, ob die Kugel vom Hindernis nach rechts oder links abgelenkt wird. Jede Programmiersprache verfügt über eine mathematische Random-, Zufallsfunktion. Von einem Startwert ausgehend erzeugt das Programm eine Dezimalzahl 0 < z < 1. Bei jedem Random-Funktionsaufruf wird normalerweise mit einem ebenfalls zufälligen Startwert die Zufallszahl generiert. Das Galtonbrett in der programmierten Animation kann als eine von vielen Methoden zeigen, wie zufällig gut die verwendete Random-Funktion arbeitet. Bildet sich als Ergebnis nach einiger Zeit eine symmetrische, glockenförmige Verteilung, dann ist der Zufall nicht manipuliert und optimal statistisch verteilt.
Der Videoclip zeigt eine Simulation des Galtonbretts. Für die ersten 10 Kugeln läuft das Video kontinuierlich. Danach werden die Ergebnisse bis zur 400. Kugel schrittweise im Abstand von 10 Kugeln angezeigt. Bis zur 1000. Kugel werden die Ergebnisse im Abstand von 50 Kugeln gezeigt. Mit der Controlleiste ist eine individuelle Steuerung möglich.
Es ist wieder mal nicht bei der spielerischen Programmierung geblieben. Irgendwie interessiert es doch zu verstehen, wie es zu dieser Verteilung kommt. Durch die 'Mathematische Formelsammlung von Lothar Papula' (10. Auflage, 2009, Verlag Vieweg+Teubner) und Dank meines engagierten Kollegen Frank Tetzlaff aus der Mathematik gibt es einen Einblick in die mathematischen Zusammenhänge der Wahrscheinlichkeiten.
Die Bernoulli-Verteilung
Das Bernoulli-Experiment beschreibt einfache Zufallsversuche, die entweder die eine oder die andere Möglichkeit als Ergebnis haben. Es handelt sich um eine Eins-Null-Verteilung, die sich zum Beispiel beim Werfen einer idealen Münze einstellt. Die Wahrscheinlichkeit, dass Zahl als Erfolg angezeigt wird, ist mit 50% ebenso groß wie der Misserfolg Wappen zu zeigen.
- Die Wahrscheinlichkeit p des Erfolgs ist p = 1/2.
- Die Wahrscheinlichkeit q des Misserfolgs ist q = 1/2.
- Die Summe beider ist p + q = 1 oder anders ausgedrückt q = 1 − p.
Das Bernoulli-Experiment kann auch auf einen idealen Würfel mit 6 Ziffern angewendet werden. Der Erfolg p eine 6 zu erhalten ist p = 1/6 und der Misserfolg q = 5/6. Die Summe ist wieder p + q = 1.
Die aktuelle Zufallsgröße X folgt einer Eins-Null-Bernoulli-Verteilung mit dem Parameter P(X=1) = p und P(X=0) = q = 1−p. Beim Galtonbrett findet eine vielfache Wiederholung mit der Bernoulli-Verteilung statt, da die Kugel nur nach rechts als Erfolg oder links als Misserfolg abgelenkt wird.
Die Binomialverteilung
Mit dem Bernoulli-Experiment steht die Binomialverteilung in enger Verbindung. Sie beschreibt eine Serie gleichartiger, sich nicht gegenseitig beeinflussender Versuche mit einer Eins-Null-Verteilung. Die Erfolgswahrscheinlichkeit sei p und n die Anzahl der Versuche. In der Binomialverteilung ist die Wahrscheinlichkeit k einen Erfolg zu erhalten definiert als:
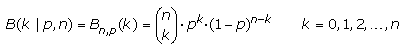
Die Wahrscheinlichkeit des Misserfolgs (1 − p) wird auch in der Binomialverteilung mit q bezeichnet mit der Summe p + q = 1. Mathematisch kann das durch die folgende Gleichung beschrieben.
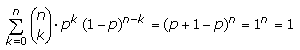
In der Gleichung erscheint die nicht so geläufige Darstellung (n über k) gelesen. Es handelt sich um eine Kurzschreibweise mit folgender Definition.
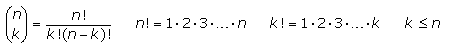
Das Pascalsche Dreieck und die Binomialkoeffizienten
Bekannter sind die beiden binomischen Formeln (a ± b)n. Errechnet man für den zunehmenden Exponenten n die Koeffizienten, die sich beim Auflösen des binomischen Ausdrucks ergeben, und schreibt sie in Dreieckform untereinander, so bildet sich das Pascalsche Dreieck. Man erkennt sehr schnell, dass sich die Koeffizienten der Folgezeile, sie beginnt und endet immer mit 1, aus der Summe der beiden darüber stehenden Ziffern errechnet.
Mit (n über k) lassen sich diese Binomialkoeffizienten ebenso errechnen. Für (4 über 2) erhält man den Binomialkoeffizienten 6, der in der (4 + 1)-ten Zeile an der (2 + 1)-ten Stelle steht.

Das Galtonbrett und die Binomialverteilung
Es besteht ein Zusammenhang zwischen dem Galtonbrett und der Binomialverteilung. In der Animation hat das Galtonbrett N = 10 Stiftreihen. Die Kugel fällt somit N-Mal zufällig entweder nach rechts oder links und endet in einem der N + 1 Fächer. Sie sind unten auf der Horizontalen als −5 ... 0 ... 5 bezeichnet. In den folgenden Betrachtungen werden sie F0 bis F10 genannt. Eine Ablenkung nach rechts wird mit 1, nach links mit 0 notiert. Der Weg w einer Kugel kann jetzt durch eine binäre Zahlenfolge beschrieben werden. Mit w = 1011000111 und w = 1010110101 landet die Kugel im Fach F6. Die Nummer des Faches entspricht der Anzahl der Einsen in der Binärzahl. Insgesamt sind bei diesem Galtonbrett 2N = 210 = 1024 unterschiedliche Wege möglich.
Soll die Kugel in das Fach Fn fallen, muss sie n-Mal nach rechts und (N-n) Mal nach links abgelenkt werden. Die Binärzahl w des Wegs enthält n-Mal die 1. Die Anzahl der Möglichkeiten in das Fach Fn zu gelangen errechnet sich durch den Binomialkoeffizienten (N über n). Er soll für das mittlere Fach F5 berechnet werden.
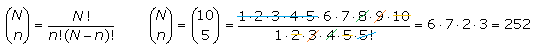
Die idealisierte Wahrscheinlichkeit nach rechts abgelenkt zu werden, soll als Erfolg mit p = 1/2 und nach links als Misserfolg mit q = 1/2 = (1 − p) gewertet werden. Die Summe ist dann p + q = 1. Zur Berechnung der Wahrscheinlichkeit sw einen der 1024 möglichen Wege zu nehmen, soll eine statistische Unabhängigkeit der zufälligen Ablenkungen definiert sein. Für einen bestimmten Weg gilt der folgende mathematische Zusammenhang:
s1010110101 = (1−p)4 · p6
Weiter oben wurde festgestellt, dass die Zahl der Einsen in der Binärzahl die Fachnummer angibt, in das die Kugel fällt. Mit der definierten Unabhängigkeit der Ablenkungen ist die Wahrscheinlichkeit der Wege sw in ein bestimmtes Fach zu gelangen immer gleich.
sw = (1−p)(N−n) · pn wobei n die Zahl der Einerzustände im Weg s ist.
Werden alle Wahrscheinlichkeiten der einzelnen Wege in ein bestimmtes Fach Fn zu gelangen addiert, dann kennt man die Wahrscheinlichkeit, mit der die Kugel dorthin gelangt. Mathematisch bestimmbar durch die folgende Gleichung. Sie gibt die Binominalverteilung der Kugeln über alle Fächer Fn an.
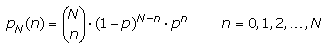
Die Summe über alle Wahrscheinlichkeiten nennt sich Binominalentwicklung und hat das Ergebnis 1.
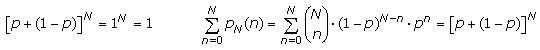
In der Statistik und hier für die Binomialverteilung ist der Erwartungs- oder Mittelwert µ und die Streuung oder Varianz σ2 definiert. Die Quadratwurzel aus der Varianz wird als Standardabweichung σ bezeichnet. Werte, die auch in der Fehler- und Ausgleichsrechnung bedeutsam sind.
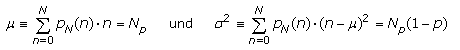
Die Binomialverteilung des idealen Galtonbretts mit p = 1/2 ergibt einen symmetrischen Spezialfall. Es gelten die folgenden Aussagen:
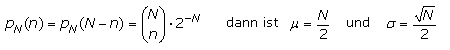
Für das oben verwendete Galtonbrett mit N + 1 = 11 Fächern kann für die Wahrscheinlichkeit 1 bei idealer Verteilung die zu erwartete Kugelzahl M · pN(n) in den einzelnen Fächern bestimmt werden. Dabei soll die Anzahl der insgesamt fallenden Kugeln M = 1024 sein.
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| pN(n) | 1 1024 |
10 1024 |
45 1024 |
120 1024 |
210 1024 |
252 1024 |
210 1024 |
120 1024 |
45 1024 |
10 1024 |
1 1024 |
| M·pN(n) | 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 |
Das sah mathematisch nicht ganz einfach aus, und vielleicht ist der folgende Weg anschaulicher. Es wird die ideale mögliche Verteilung der Kugeln beim Einlauf in das Galtonbrett und nach jeder Reihe betrachtet. Auf den Einlaufstift trifft immer genau eine Kugel. In der Folgereihe kann jeder Stift zu 50%, also mit der Wahrscheinlichkeit 1/2 getroffen werden. In der nächsten Reihe teilt sich der Wert zu je 50% auf mit der Wahrscheinlichkeit von 1/4 auf. Dabei zeigt sich, dass die mittlere Kugel zwei Mal 1/4 Anteile hat. Dieser Wert teilt sich in der nächsten Reihe wieder an jedem Stift mit 50% auf. Das ist eine Wahrscheinlichkeit von 1/8 mit der jeder Stift getroffen wird. Damit entstehen für die ersten Stiftreihen bildlich dargestellt die folgenden Wahrscheinlichkeiten.
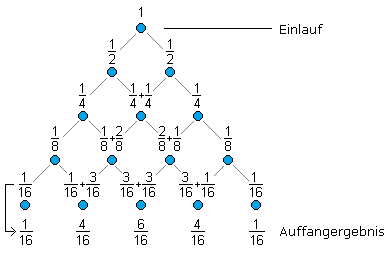
Im zusammengefassten Auffangergebnis entsprechen die Zähler den Binomialkoeffizienten nach dem Pascalschen Dreieck. Die Nenner sind Potenzen von 2, die sich aus den Wahrscheinlichkeiten mit p = q = 1/2 nach jeweils einer Seite zu fallen ergeben. Es bestätigt sich die oben angewendete Gleichung für pN(n). Die allgemeine Gleichung zur Berechnung der Binomialkoeffizienten wird beispielhaft für die 4. Stiftreihe (n = 4) und der Spaltenzählung von links mit k = 0 ... 4 gezeigt.
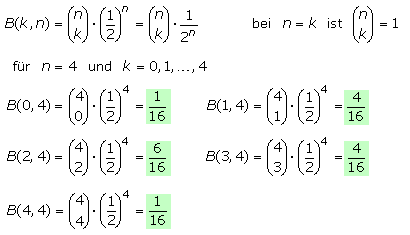
Mittelwert und Varianz für das Experiment Galtonbrett
In der Zwischenzeit, die man vielleicht oder hoffentlich mit dem Lesen und Verstehen der mathematischen Zusammenhänge verbracht hat, sind bestimmt viele Kugeln im oben laufenden Galton-Experiment gefallen. Das Experiment zählt sowohl die Anzahl der gefallenen Kugeln als auch die Verteilung in den einzelnen Fächern. Die Darstellung erfolgt zum mittleren Fach symmetrisch, daher hat es die Fachnummer 0. Nach links und rechts bleiben jeweils 5 Fächer. Die Zählung von links nach rechts lautet folglich −5 ... 0 ... 5
Berechnung des Mittelwerts
Gesucht ist der Erwartungswert E(X) einer diskreten Zufallsvariablen X. Die Auswertung erfolgt, indem man die Kugelzahl in jedem Fach mit der Fachnummer multipliziert. Alle Ergebnisse werden addiert und die Summe durch die Gesamtzahl der Kugeln dividiert. Es handelt sich hierbei um einen bewerteten Mittelwert, wie er auch zur Bestimmung einer Durchschnittszensur bei Klausuren angewendet wird.
Die folgende Tabelle zeigt die Ergebniswerte für einen Galtonversuch mit N=256 gefallenen Kugeln und −5 ≤ i ≥ 5. Zum Vergleich zeigen die beiden letzten Tabellenzeilen die Berechnung für 0 ≤ i ≤ 10, der nach rechts in nur positive Fachzahlen verschobenen Verteilung. Beide Ergebnisse zeigen, dass sich zur Mitte hin die meisten Kugeln angesammelt haben. Bei ideal symmetrischer Verteilung wäre der Mittelwert 0 oder 5.
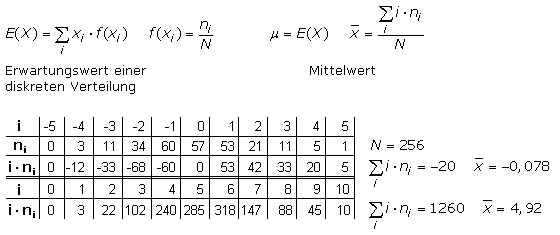
Berechnung der Varianz und Standardabweichung
Man ermittelt für jedes Fach i die Abweichung vom Mittelwert und multipliziert mit der Anzahl ni der Kugeln im Fach. Diese Einzelergebnisse dividiert man durch die Gesamtzahl aller Kugeln und erhält die Streuung s2 oder Varianz σ2. Die Quadratwurzel aus der Varianz ergibt die Standardabweichung.
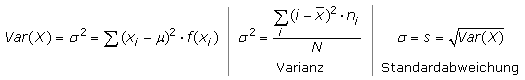
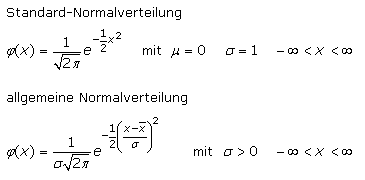
Die Dichtefunktionen der Normalverteilungen
In der Animation werden nach jeder Kugel die Werte für den Mittelwert und der Standardabweichung angezeigt. Im Hintergrund wird die standardisierte Normalverteilung (grün) der Gaußschen Normalverteilung mit den Werten µ = 0 und σ = 1 dargestellt. Die aus dem laufenden Versuch folgende allgemeine Normalverteilung (orange) gleicht sich mit zunehmender Kugelzahl der Glockenkurve an. Die Standardabweichung ist auch bei einigen Tausend Kugeln größer 1 und liegt zwischen 1,6 > s > 1,5. Bei beiden Kurven handelt es sich um Dichtefunktionen der Normalverteilungen mit einer stetigen Zufallsvariablen X.