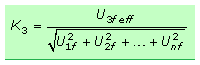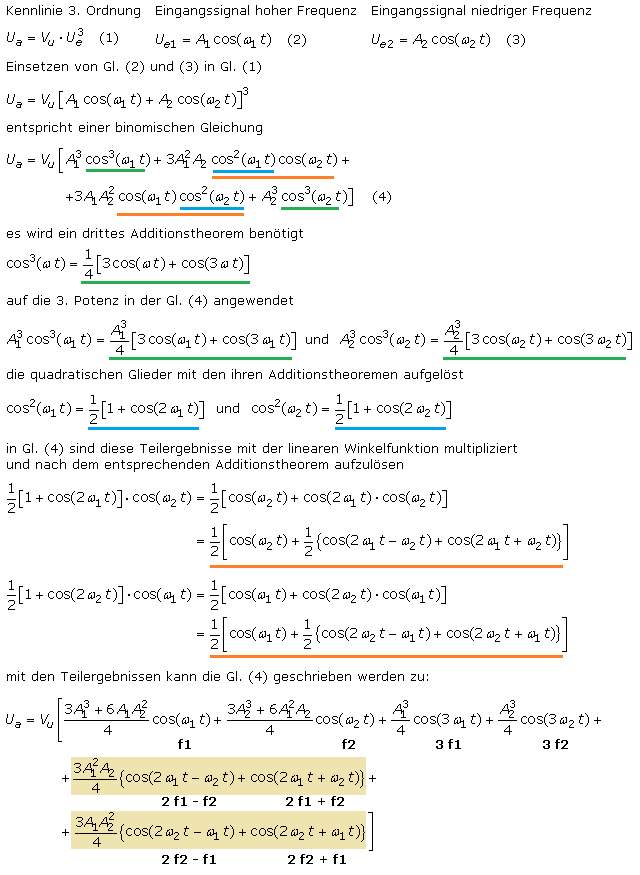Signalverzerrungen und der Klirrfaktor

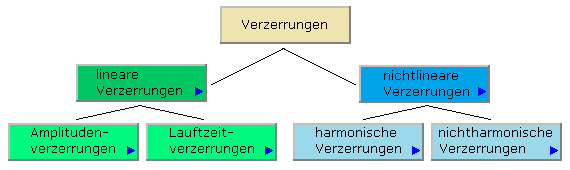
Ist nach dem Durchlaufen einer elektronischen Baugruppe das Ausgangssignal bis auf einen linearen Verstärkungsfaktor identisch mit dem Eingangssignal, so liegt eine verzerrungsfreie Signalverarbeitung vor. Ein Idealfall, der fast nie zu erreichen ist, da in der Übertragungskette das Signal von kapazitiven, induktiven und nicht linear arbeitenden Schaltelementen beeinflusst wird. Signalverzerrungen werden in lineare und nichtlineare Verzerrungen unterschieden und lassen sich, wie in der verweissensitiven Skizze dargestellt, weiter aufteilen.

Lineare Verzerrungen

Elektronische Baugruppen und Schaltungen, die für jede Frequenz eine linear verlaufende Spannungs- oder Stromkennlinie aufweisen, verursachen lineare Verzerrungen. Sie werden in der englisch sprachigen Literatur als linear distortion oder frequency response bezeichnet. Lineares Verhalten haben ohmsche Widerstände, Kondensatoren und Spulen und die Zusammenschaltungen gleichartiger Bauteile. Bei höheren Frequenzen können lineare Verzerrungen durch den Schaltungsaufbau, dem Platinenlayout sowie internen Schaltkapazitäten der Transistoren und integrierten Schaltkreisen verursacht werden. Letztere werden oft als parasitäre Kapazitäten bezeichnet und verursachen frequenzabhängige Rückkopplungen.

Bei linearen Verzerrungen sind im Ausgangssignal nur die Amplituden der im Eingangssignal auftretenden Frequenzen verändert. Verschiedene Frequenzbereiche können mit unterschiedlichen Laufzeiten am Ausgang erscheinen. Die Ein- und Ausgangssignale sind dann zueinander in ihrer Phasenlage verschoben. Im Ausgangssignal treten keine neuen Frequenzen auf. Der Nachweis erfolgt mit Frequenzanalysatoren durch eine Signalanalyse nach Fourier.

Jedes periodische Signal lässt sich nach Fourier aus der Grundschwingung und falls notwendig aus den ganzzahligen Vielfachen, den Oberschwingungen darstellen. Die Grundschwingung, auch 1. Harmonische genannt, besitzt die höchste Amplitude. Die Amplituden der Oberschwingungen nehmen zu höheren Frequenzen hin kontinuierlich ab. In der Zählweise ist die 2. Harmonische somit die 1. Oberschwingung usw. Das Ausgangssignal weist lineare Verzerrungen auf, wenn einzelne Harmonische oder ganze Frequenzbereiche des Eingangssignals durch linear arbeitende Schaltelemente unterschiedlich beeinflusst werden.

Amplitudenverzerrungen

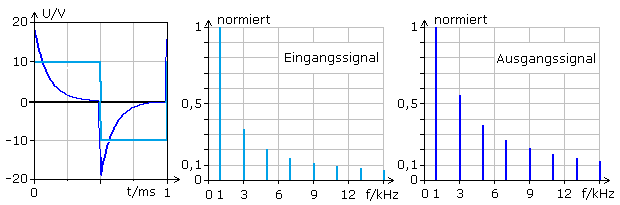
Das Ausgangssignal des zu untersuchenden Zweitors (Vierpols) zeigt einen frequenzabhängigen Amplitudengang. Es treten Amplituden- oder Dämpfungsverzerrungen (engl. attenuation distortion) auf. Die folgenden Diagramme zeigen Beispiele linearer Verzerrungen für eine Tiefpass- und gleichartig dimensionierte Hochpassschaltung. Das Eingangssignal ist ein symmetrisches Rechtecksignal. Die gewählte Grundfrequenz beträgt 1 kHz. Im Eingangssignal sind nach Fourier alle ungeraden Harmonischen mit abnehmender Amplitude enthalten.

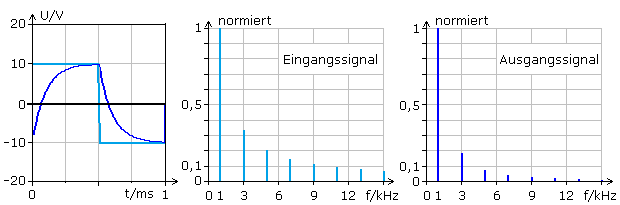
Im Zeitdiagramm ist das Ausgangssignal (dunkelblau) eindeutig verzerrt. Die Spektralanalyse zeigt, dass die Amplituden aller höheren Harmonischen im Vergleich zum Eingangssignal (hellblau) deutlich niedriger sind. Der Frequenzbereich oberhalb der 5. Harmonischen ist schon vernachlässigbar. Neue Frequenzen treten im Spektrum nicht auf. Das Eingangssignal wurde vom Tiefpass linear verzerrt.

Das Ausgangssignal nach einem Hochpass zeigt deutlich höhere Amplituden für die im Eingangssignal enthaltenen Oberfrequenzen. Das Zeitdiagramm des Ausgangssignals ist völlig anders verzerrt. Da im Frequenzspektrum keine neuen Frequenzen auftreten, handelt es sich auch hier um lineare Verzerrungen.

Beide Beispiele zeigen Amplitudenverzerrungen, die je nach Anwendungsbereich gewünscht und gezielt herbeigeführt oder unerwünscht und somit störend sind. Die Klangbeeinflussung in der Audiotechnik durch Equalizer oder die einfachere Tiefen- und Höhenverstellung mittels Shelvingfilter verwendet Tiefpass-, Hochpass- und Bandpassschaltungen und erzeugt gewünscht lineare Verzerrungen. Audioverstärker mit zu geringer Bandbreite klingen weich, es fehlt die Brillanz, die von den hohen Frequenzbereichen ausgeht. Auch die Harmonischen oberhalb des Hörbereichs von 20 kHz tragen zur hörbaren Klangqualität bei.

Werden hochfrequente oder digitale Datensignale leitungsgebunden über lange Strecken gesendet werden, so entstehen durch den Tiefpasscharakter der Leitung lineare Verzerrungen. Diese Bandbreitenbegrenzung ist hier störend, da durch sie eine eindeutige Signalerkennung am Ausgang erschwert oder verhindert wird.

Laufzeitverzerrungen

Jedes Eingangssignal benötigt bis zum Ausgang einer elektronischen Baugruppe eine bestimmte, wenn auch sehr kurze Zeit. Diese Laufzeiten sind von der Frequenz abhängig und bei der gleichzeitigen oszillografischen Darstellung des Eingangs- und Ausgangssignals erkennt man sie als Phasenverschiebung. Die Laufzeitverzerrungen können daher auch als Phasenfehler oder Phasenverzerrungen (engl. phase distortion) bezeichnet werden.

Phasenfehler treten insbesondere bei aktiven Baugruppen wie Verstärkern auf. Verstärker mit einer kurzen Signalanstiegzeit (slew rate), verursachen innerhalb ihrer Arbeitsbandbreite nur geringe Laufzeitverzerrungen. Unabhängig davon gilt für jeden Verstärker das Bandbreite-Verstärkungsprodukt, das einen konstanten Wert darstellt. Aus diesem Grund lassen sich bei linearen Verzerrungen die Amplituden- und Phasenverzerrungen nicht völlig voneinander trennen. Mit zunehmender Verstärkung verringert sich die nutzbare Bandbreite, sodass die hohen Frequenzanteile des Eingangssignals im Ausgangssignal mit geringerer Amplitude auftreten.

Fast alle Filterschaltungen erzeugen Phasenverschiebungen. In der Audiotechnik lassen sich Frequenzgänge durch Equalizer normalisieren und vorhandene Amplitudenfehler im Hörbereich ausgleichen. Fast immer wird dabei der Phasenfehler zunehmen. Bei der Dimensionierung von Lautsprecherweichen spielt die Kenntnis der Frequenzlaufzeiten zum Hoch-, Mittel- und Tieftonchassis eine bedeutende Rolle für den endgültig abgestrahlten Klang.

Nichtlineare Verzerrungen

Elektronische Baugruppen mit gekrümmten, nicht linearen Kennlinien verursachen nichtlineare Verzerrungen. Im Ausgangssignal lassen sich immer Frequenzen nachweisen, die im Eingangssignal nicht vorhanden sind. Dieser Effekt kann sehr wohl beabsichtigt sein, denn alle Modulationsvorgänge finden an gekrümmten Kennlinien statt und lassen sich somit als nichtlineare Verzerrung (engl. nonlinear distortion) erklären.

Von harmonischen Verzerrungen spricht man, wenn die neuen Frequenzen als ganzzahlige Vielfache der Grundfrequenz auftreten. Die Amplituden der höheren Harmonischen oder Oberwellen nehmen normalerweise mit zunehmender Frequenz stetig ab. In der Audiotechnik werden nichtlineare Verzerrungen aus überwiegend geradzahligen Harmonischen angenehmer empfunden. Ihre Frequenzen bilden vom Grundton ausgehend einen Oktavabstand. Die erste höhere Oktave einer Grundtonfrequenz hat die doppelte Frequenz. Frequenzmuster mit ganzzahligen Vielfachen im Oktavabstand klingen für menschliche Ohren angenehmer. Man ist daher bestrebt, die Amplituden der ungeradzahligen höheren Harmonischen möglichst gering zu halten.

Verstärkerbaugruppen wie bipolare Transistoren, Feldeffekttransistoren und Elektronenröhren haben unterschiedlich gekrümmte Steuerkennlinien. Eingangssignale mit größeren Amplituden werden dann auch bei einem optimal berechneten Arbeitspunkt nicht mehr symmetrisch verstärkt. Das Ausgangssignal ist nach einer Halbwelle hin stärker verzerrt. Ein zu großes Eingangssignal übersteuert den Verstärker, wobei das Ausgangssignal zu beiden Halbwellen abgeflacht und begrenzt wird. Im verzerrten Signal lassen sich durch die Frequenzanalyse nach Fourier neue Harmonische der Grundfrequenz nachweisen.

Auch andere Baugruppen mit gekrümmten Kennlinien wie Übertragertransformatoren, Tonköpfe und Magnetspeicher, Dioden und VDR-Widerstände bewirken eine Signalverzerrung. Alle diese Verzerrungen werden als nichtlineare Verzerrung bezeichnet. Das Bild zeigt die Oberwellenanteile eines Verstärkers mit nicht optimal eingestelltem Arbeitspunkt.

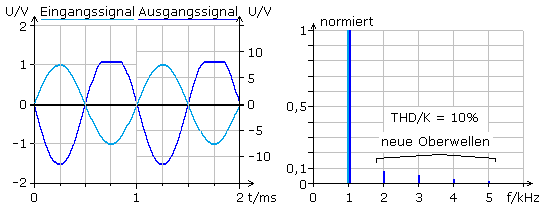
Das 1 kHz Audioreferenzsignal (hellblau) ist praktisch frei von Oberwellen und besteht aus der Grundfrequenz oder 1. Harmonischen. Das einseitig verzerrte Ausgangssignal (dunkelblau) zeigt im Spektrum rechts die neu hinzugekommenen ganzzahligen höheren Harmonischen. Das Ausgangssignal weist nichtlineare Verzerrungen mit einem Gesamtamplitudenanteil von 10% auf.

Der Verzerrungsfaktor oder Klirrfaktor

Durch nichtlineare Verzerrungen und dem Auftreten höherfrequenter Harmonischer klingt ein Signal schrill oder klirrend. Traditionell werden nichtlineare Verzerrungen mit dem Klirrfaktor k (engl. distortion factor) angegeben. Eine ähnliche Kenngröße wurde später als THD (total harmonic distortion) eingeführt. Beide Verzerrungsfaktoren stellen ein Spannungsverhältnis dar.

Der Verzerrungsfaktor ist immer kleiner als eins. Die Angabe erfolgt meistens in Prozent. Für THD-Werte bis 5% genügt die oben vorgestellte verkürzte Gleichung. Die Verzerrung kann auch als Klirrdämpfung (engl. distortion attenuation) oder als Klirrdämpfungsmaß in dB angeben werden, wobei der Wert stets negativ ist.

Ein gutes Übertragungsverhältnis ist noch bei einem Klirrfaktor von 5% gegeben. Hi-Fi-Verstärker dürfen nach DIN 45500 höchstens 1% aufweisen, wobei selbst einfache Geräte mit Faktoren <0,1% besser sind. Das ungeschulte Gehör erkennt am reinen Ton einen Klirrfaktor ab 3%, mit etwas Übung ab 1%, während bei einer Musik- oder Sprachdarbietung das sichere Erkennen erst ab 7% gegeben ist.

Die harmonischen Verzerrungen sind von der Größe der Eingangsspannung und von der Frequenz abhängig. Geeignete Gegenkopplungsmaßnahmen in der Verstärkerschaltung minimieren den Verzerrungsfaktor. In der Magnetaufzeichnungstechnik ist die dritte Oberwelle besonders ausgeprägt. Die Magnetisierungskurve entspricht einer Kennlinie in der mathematisch 3. Potenz, einer kubischen Kennlinie. Durch sie ist die dritte Oberfrequenz und somit die 4. Harmonischen bevorzugt. In diesen Fällen wird die Güte des Ausgangssignals nicht durch den Klirrfaktor, sondern einen Klirrkoeffizienten beurteilt. Der kubische Klirrkoeffizient oder K3-Faktor der Magnettonaufzeichnung errechnet sich mit der nachstehenden Gleichung:

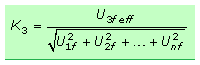
Entsteht der Klirrfaktor nur durch geradzahlige Harmonische, so hört sich das Signal bei gleichem Klirrfaktor weniger verzerrt an, als für ungeradzahlige Harmonische. Tonfolgen im Oktavabstand, also bei doppelter Frequenz oder dem ganzzahligen Vielfachen einer Oktavfrequenz, werden vom Ohr als harmonisch klingender empfunden.

Mit einer Klirrfaktormessbrücke sind harmonische Verzerrungen direkt bestimmbar. Dieses Gerät besitzt einen oder mehrere umschaltbare Sinusgeneratoren fester Messfrequenzen mit vernachlässigbar kleinen Eigenklirrfaktoren. Das Sinussignal wird dem zu untersuchenden Messobjekt, beispielsweise einem Audioverstärker, als Eingangssignal zugeführt. Dessen Ausgangssignal wird von der Klirrfaktormessbrücke analysiert. Im Messverfahren wird aus dem Verstärkersignal die Frequenz des Eingangssignals ausgefiltert. Der Effektivwert des Restsignals ist dann die Summe aller im Verstärker neu entstandener Oberfrequenzen. Das Verhältnis des Restsignals zum Gesamtsignal ergibt den Klirrfaktor. Die Messungen berücksichtigen meisten nur die ersten drei bis fünf Oberfrequenzen entsprechend der 4. bis 6. Harmonischen.

Für eine sehr genaue Bestimmung muss ein Frequenzspektrenanalysator verwendet werden. Dieses Messgerät hat eine Reihe durchstimmbarer schmalbandiger Schwingkreise sehr hoher Güte, die im ganzzahligen Frequenzverhältnis stehen. Die Resonanzspannungen werden gemessen und zum Gesamtklirrfaktor THD/K ausgewertet.

Nichtharmonische Verzerrungen

Die meisten zu verarbeitenden Signale sind ein Gemisch vieler verschiedener Frequenzen. Beim Durchlaufen von Verstärkern oder anderen elektronischen Baugruppen kann es an deren nichtlinearen Kennlinien zwischen einzelnen Signalfrequenzen zur Amplitudenmodulation kommen. Im Ausgangssignal erscheinen dadurch neue Frequenzen, die im Eingangssignal fehlen. Sie stehen zueinander in keinem harmonischen Verhältnis und werden in Audiosignalen vom Ohr als Disharmonien wahrgenommen und als besonders störend empfunden. Bezogen auf die zu untersuchende Schaltung und die Messmethode, werden nichtharmonische Verzerrungen als Differenztonverzerrungen oder Intermodulationsverzerrungen bezeichnet.

Differenztonverzerrungen

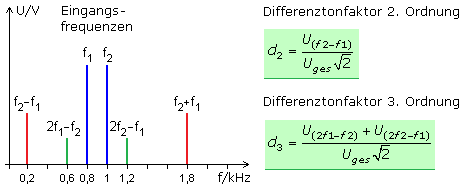
Die Nichtlinearität eines schmalbandigen Zweitors führt zu einem hohen Differenztonfaktor. Als Eingangssignal werden zwei gegeneinander entkoppelte, unterschiedliche Sinusfrequenzen gleicher Amplitude benutzt. Am Ausgang werden die Effektivspannungen der Differenzsignale gemessen und ins Verhältnis zum Effektivwert des gesamten Frequenzgemisches gesetzt. Von Interesse ist der Differenztonfaktor zweiter Ordnung d2. Er wird an Bauteilen mit unsymmetrischer parabelförmiger Kennlinie verursacht. Eine symmetrische Kennlinie liefert Werte für den Differenztonfaktor dritter Ordnung d3. Je geringer der Frequenzabstand der Eingangssignale ist, desto weiter sind die Differenzsignale zu niedrigen Frequenzen verschoben und die ebenfalls entstehenden Summenfrequenzen liegen außerhalb der Bandbreite des Zweitors.

Intermodulationsverzerrungen

Im Bereich der Elektroakustik kommt ein spezielles Zweitonmessverfahren zur Anwendung. Nach der DIN 45500 Hi-Fi-Norm werden an den Eingang des Messobjekts die beiden Sinusfrequenzen 250 Hz und 8000 Hz im Amplitudenverhältnis 4:1 gelegt. Zur Auswertung wird die Summe der am Ausgang neu auftretenden Effektivwerte der Summen- und Differenzfrequenzen als Modulationsprodukte in Bezug zum Effektivwert der höheren Signalfrequenz gesetzt. Berücksichtigt werden auch hier meistens nur Intermodulationsfaktoren der zweiten und dritten Ordnung. Eine allgemeingültige Gleichung zur Berechnung des Intermodulationsfaktors kann durch das Einfügen eines Abstandsfaktors q aufgestellt werden. Der Abstandsfaktor steht für den ganzzahligen Abstand der Seitenfrequenzen bezogen auf die höhere Messfrequenz f2, die moduliert wird.

Die Berechnung kann wahlweise mit den Effektiv- oder Spitzenwerten erfolgen. Für die beiden einfachen Gleichungen oben ist die geometrische Addition nicht notwendig, da alle Signale untereinander eine feste Phasenlage aufweisen. Das Ergebnis wird in Prozent oder Dezibel ausgegeben. Bei guten Audioverstärkern ist der Intermodulationsfaktor kleiner 0,5%.

Mathematischer Hintergrund zur IM

Im Kapitel zur Amplitudenmodulation an der Diodenkennlinie wird gezeigt, dass die Nichtlinearität mathematisch durch eine Potenzreihe beschrieben werden kann. Sie enthält neben dem quadratischen Glied auch Glieder höherer Ordnung, durch die weitere Mischprodukte entstehen können. In der Potenzreihe nehmen die Amplituden mit zunehmender Ordnung schnell ab. Zur Bestimmung der Intermodulationsverzerrungen (IM) genügt es daher, die Intermodulationsprodukte der zweiten IM2, maximal dritten Ordnung IM3 zu berücksichtigen.

Intermodulation 2. Ordnung

Vor der Modulation überlagern sich beide Eingangssignale additiv. Mit dem Summensignal entstehen an der nichtlinearen Übertragungsfunktion neue Frequenzen, darunter wie bei der Amplitudenmodulation die Differenz- und Summenfrequenzen. Die Intermodulation entspricht mathematisch einer Multiplikation der Frequenzen.

Mit einem Schaltungsaufbau im Labor oder einfacher durch ein Simulationsprogramm am PC kann die Intermodulation untersucht und mit dem mathematischen Ergebnis verglichen werden. Als Eingangsfrequenzen werden 1 kHz und 10 kHz mit gleicher Amplitude an einem Widerstandsnetzwerk linear addiert. Das Summensignal geht an beide Eingänge eines Vollmultiplizierers mit der Verstärkung 1. Dargestellt werden die Oszillogramme und Fourieranalysen der Signale.

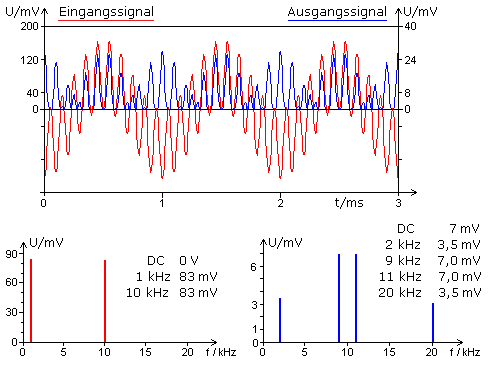
Das Oszillogramm des Eingangssignals (rot) hat keinen Gleichspannungsanteil und verläuft symmetrisch zur Nulllinie, während das Ausgangssignal (blau) mit seinem DC-Anteil oberhalb der Nullachse liegt. Die ermittelten Werte der Fourieranalyse des Ausgangssignals entsprechen der oben hergeleiteten Gleichung. Der neue Gleichspannungsanteil kann den Arbeitspunkt der Schaltung verschieben und dadurch den Intermodulationsfaktor vergrößern.

Intermodulation 3. Ordnung

Die beiden additiv überlagerten Eingangssignale werden durch einen Kennlinienverlauf 3. Grades verzerrt. Mathematisch ist die dritte Potenz zu berechnen, ein Vorgang mit viel schriftlichem Rechenaufwand.

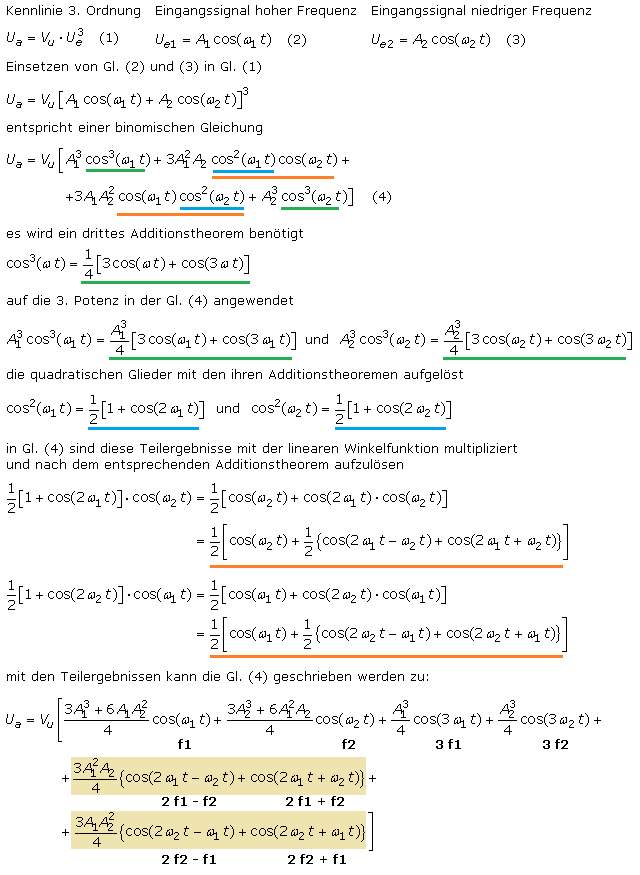
Die beiden farbig hinterlegten Ausdrücke der endgültigen Gleichung stehen für Intermodulationsprodukte. Der Cosinus ist eine symmetrische Funktion und es gilt cos(x) = cos(−x). Angewendet auf cos(2·f2 − f1) erhält man cos(f1 − 2·f2). Dieser bildet mit cos(f1 + 2·f2) das Wertepaar im Zähler der Bestimmungsgleichung des Intermodulationsfaktors.

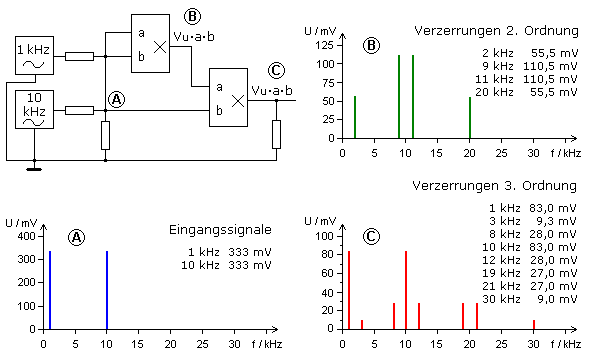
Die Eingangsfrequenzen 1 kHz und 10 kHz erzeugen an einer Kennlinie 3. Ordnung (kubisch) weitere Frequenzen mit 3 kHz, 30 kHz, 8 kHz, 12 kHz, 19 kHz und 21 kHz. Mit einer Simulationssoftware konnte die Spektralverteilung mit deren Amplitudenwerten nachgewiesen werden. Zwei Sinussignale mit 1 kHz und 10 kHz wurden linear addiert und als Eingangssignal auf einen Multiplizierer gegeben. Das Ausgangssignal bildet mit dem Additionssignal die Eingangssignale des zweiten Multiplizierers. Sein Ausgangssignal entspricht der dritten Potenz des Eingangssignals. Das Bild zeigt die Fourieranalyse mit den gemessenen Amplitudenwerten. Sie stimmen mit den Verstärkungsfaktoren der oben hergeleiteten Gleichung überein.