Determinanten in der Mathematik

Eine Determinante ist immer eine quadratische Anordnung mit einer reellen oder komplexen Zahl als Lösungswert. Der Ausdruck kommt aus dem Lateinischen mit der Bedeutung: abgrenzend, bestimmend. Mathematisch ist die Determinante eine Rechenoperation, um den Wert einer zugeordneten quadratischen Matrix zu bestimmen. Das Ergebnis ist eine skalare Größe. Determinanten sind ein geeignetes Mittel zur programmierten Lösung linearer Gleichungssysteme. Rechenprogramme können Gleichungen und Formeln nicht so wie wir zum Auffinden von Lösungen umstellen. Das rekursive Anwenden einfacher Rechenregeln auf zweidimensionale Arrays, den Determinanten, ist für Computerprogramme und Menschen leicht durchführbar.

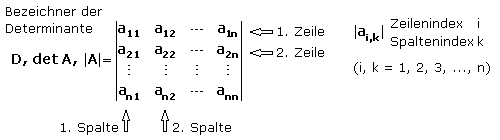
Die Determinante erhält einen Großbuchstaben als Bezeichner. Steht sie mit einer Matrix A in Verbindung, so kann sie auch als det A oder |A| bezeichnet werden. Die Elemente der Determinante sind in Zeilen, hier Reihen genannt und Spalten zwischen senkrechten Strichen angeordnet. Die Indizierung der Elemente entspricht der einer Matrix.

Zweireihige Determinante

Eine mathematische Funktion, die als Ergebnis einen reellen Zahlenwert hat, kann als zweireihige Determinante geschrieben werden. Sie enthält 4 Elemente, angeordnet zu zwei Reihen und zwei Spalten. Wie bei der quadratischen Matrix beschrieben, hat die Determinante eine Haupt- und Nebendiagonale. Der Wert der Determinante errechnet sich aus dem Produkt der Elemente auf der Hauptdiagonalen, von dem das Produkt der Elemente der Nebendiagonalen abgezogen wird. Mit zweireihigen Determinanten lassen sich lineare Gleichungen mit zwei Unbekannten lösen, solange nicht alle Koeffizienten der Unbekannten den Wert null haben.

Dreireihige Determinante und die Sarrus-Regel

Die Elemente einer dreireihigen Determinanten sind in drei Reihen (Zeilen) zu drei Spalten angeordnet. Das Ergebnis ist eine reelle Zahl, die nach der Regel von Sarrus sehr übersichtlich berechnet werden kann. Die Determinante wird um ihre ersten zwei Spalten erweitert, sodass man drei Haupt- und Nebendiagonalen einzeichnen kann. Der Wert der Determinante errechnet sich aus der Summe der Produkte mit den Elementen der Hauptdiagonalen, von der die Summe der Produkte mit den Elementen auf den Nebendiagonalen subtrahiert wird. Die Sarrus-Regel kann nicht auf Determinanten höherer Ordnung angewendet werden. Aus diesen sind so lange Unterdeterminanten zu entwickeln, bis sie in zwei- oder dreireihige Determinanten überführt sind, die dann berechnet werden.

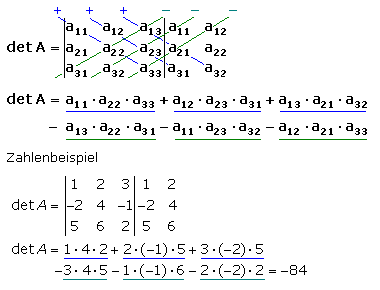
Unterdeterminante

Aus Determinanten ab der 3. Ordnung lassen sich Unterdeterminanten erstellen. Man streicht in der Determinante eine beliebige Zeile und Reihe. Die verbleibenden Elemente bilden eine Unterdeterminante, die eine Ordnung niedriger ist. Das folgende Bild zeigt die Vorgehensweise an einer dreireihigen Determinante durch Streichen der 1. Zeile und 2. Spalte.

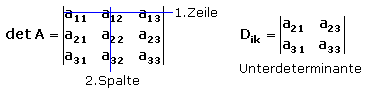
Es ist ersichtlich, dass sich aus der gezeigten Determinante 3. Ordnung insgesamt 9 Unterdeterminanten erstellen lassen. Mithilfe von Unterdeterminanten kann der Wert der Determinante ermittelt werden. Dazu ist ein Faktor notwendig, der für das Element am Schnittpunkt der weggestrichenen Zeile und Spalte steht.

Algebraisches Komplement – Adjunkte

Ein algebraisches Komplement ist eine rechnerische Ergänzung. Für das aus der Determinante D ausgewählte Element aik ist die Adjunkte Aik, die mit einem Vorzeichenfaktor multiplizierte Unterdeterminante Dik. Der Faktor errechnet sich aus (−1)^i+k, den Parametern der i-ten Zeile und k-ten Spalte, wo das Element aik steht. Der Vorzeichenfaktor kann recht einfach einem Schachbrettmuster entnommen werden.

Entwicklungssatz nach Laplace

Einer Matrix vom Typ (1,1) kann eine 1-reihige Determinante zugewiesen werden. Nach den Ausführungen weiter oben ist sie die Funktion, die den Wert der Matrix berechnet. Das Ergebnis ist, wie bei den Matrizen beschrieben, als skalare Größe definiert.

Matrix: A = ( a₁₁ ) ihre Determinante D = det A = | a₁₁ | = a₁₁ ein Skalar

Mit einer n-reihigen Determinante wird der Wert einer quadratischen Matrix berechnet. Die Determinante wird rekursiv nach einer Entwicklungsformel berechnet. Mit gleichartig sich wiederholenden Verfahren lassen sich mathematische Probleme sehr gut mit programmierten automatischen Auswertungen lösen. Nach Laplace kann die Entwicklung nach jeder beliebigen Zeile oder Reihe der Determinante durchgeführt werden. Das folgende Beispiel zeigt die Entwicklung allgemein nach den Elementen der i-ten Zeile oder den Elementen der k-ten Spalte. Es folgt ausführlich die Entwicklung nach der 1. Zeile am Beispiel einer dreireihigen Determinante.

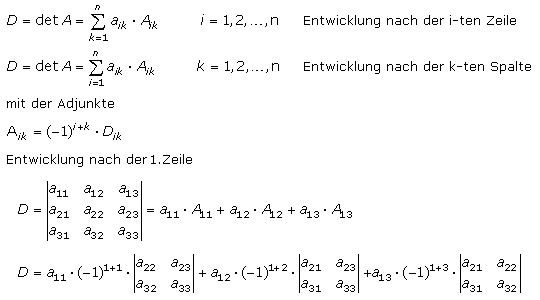
Wendet man die Regel nach Sarrus auf eine dreireihige Determinante an und vergleicht das Ergebnis mit dem aus einer beliebigen Entwicklung für diese Determinante, so sind die Ergebnisse identisch. Jede n-reihige Determinante kann so auf (n−1)-reihige Unterdeterminanten entwickelt werden, um letztlich 3-reihige Unterdeterminanten zu erhalten, die nach der Sarrus-Regel berechnet werden. Damit die Anzahl der Unterdeterminanten klein bleibt, versucht man die Entwicklung nach einer Zeile oder Spalte mit möglichst vielen Nullen durchzuführen.

Eigenschaften n-reihiger Determinanten

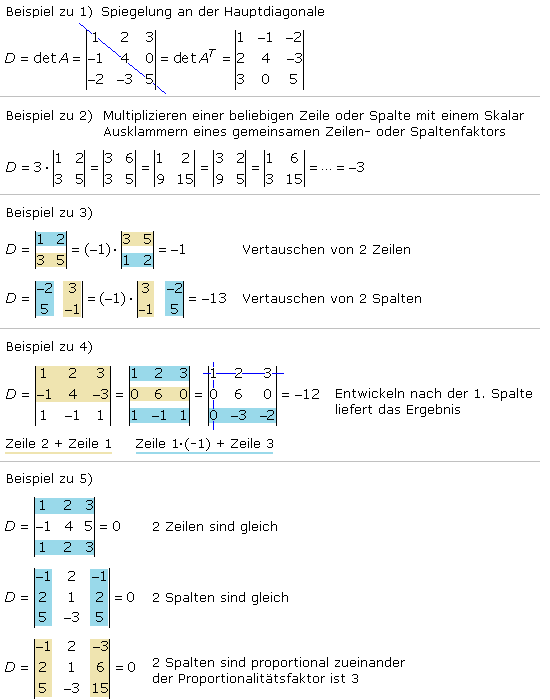
1. Der Wert einer Determinante bleibt gleich, wenn ihre Zeilen als Spalten und Spalten als Zeilen geschrieben werden. Das entspricht der Spiegelung an der Hauptdiagonalen mit dem Ergebnis der transponierten Determinante.
2. Haben alle Elemente einer Zeile oder Spalte einen gemeinsamen Faktor, so kann er ausgeklammert als Skalar vor die Determinante gesetzt werden. Ebenso kann ein skalarer Faktor vor einer Determinante mit allen Elementen einer beliebigen Zeile oder Spalte multipliziert werden.
3. Vertauscht man in einer Determinante zwei Zeilen oder Spalten, dann ändert sich das Vorzeichen der Determinante.
4. Der Wert einer Determinante bleibt gleich, wenn man zu den Elementen einer Zeile oder Spalte die Elemente oder deren Vielfaches einer anderen Zeile oder Spalte addiert.
5. Der Wert einer Determinante ist null, wenn
   • alle Elemente einer Zeile oder Spalte den Wert null haben;
   • zwei Zeilen oder Spalten gleich sind;
   • zwei Zeilen oder Spalten zueinander proportional sind.

Vor der Berechnung einer n-reihigen Determinante wird man versuchen, durch das Anwenden der Rechenregeln aus den oben beschriebenen Eigenschaften, dass möglichst viele Elemente einer Zeile oder Reihe den Wert null erhalten. Die Entwicklung nach Laplace erfolgt dann nach dieser Zeile oder Spalte, da weniger Unterdeterminanten entstehen. Mithilfe von Determinanten kann das Lösen linearer Gleichungssysteme programmiert erfolgen, ohne Gleichungssysteme umzustellen und neu zu schreiben.