Fourier-Transformation
Mit der Fourier-Transformation (FT), hier speziell als Fourier-Analyse, kann ein von der Zeit abhängiges, normalerweise periodisches Signal als Überlagerung der vorkommenden periodischen Einzelfrequenzen dargestellt werden. Das Ausgangssignal in seiner Amplituden-Zeitabhängigkeit wird in ein Amplituden-Frequenzspektrum überführt. Oft ist es von Interesse ein periodisches Signal hinsichtlich der darin vorkommenden Frequenzen und ihrer Amplituden zu untersuchen. Sollen beispielweise Rechteckpulse oder Sägezahnsignale von elektronischen Schaltungen möglichst unverzerrt verarbeitet werden, so muss die Elektronik eine bestimmte Bandbreite haben. Es genügt nicht, nur die aus dem Amplituden-Zeitdiagramm ablesbare Grundfrequenz eines zusammengesetzten Signals zu kennen. Erst das zugehörige Amplituden-Frequenzdiagramm zeigt die anderen im Signal vorhandenen Frequenzen mit ihren Amplitudenanteilen.
Der Mathematiker Fourier hat herausgefunden, dass jedes periodische Signal durch eine Summe unendlich vieler Sinus- und Cosinusschwingungen und falls notwendig einem zusätzlichen Gleichanteil dargestellt werden kann. Eine Funktion f(x) ist periodisch, wenn sich ihre Funktionswerte nach einer Verschiebung um 2π (2Pi) für alle x-Werte im Definitionsbereich nicht ändern. Für 2Pi-periodische Funktionen gilt f(x) = f(x + 2π). Ist f(x) eine stetige monotone Funktion und im Intervall −π ≤ x ≤ π gleich 0 ≤ x ≤ 2·π integrierbar, so kann die Funktion als unendliche trigonometrische Funktionsreihe geschrieben werden.
In Formelsammlungen sind für eine periodische Funktion f(t) zwei unterschiedliche Schreibweisen zur allgemeinen Darstellung der reellen Fourierreihe zu finden. Sie werden als Summe von Kosinus- und Sinusfunktionen mit ihren konstanten Koeffizienten und der ganzzahligen Laufzahl n geschrieben. Wird das Zeitdiagramm eines periodischen Signals mithilfe der Fourier-Transformation in das Frequenzspektrum überführt, dürfen im Spektrum nur ganzzahlige Vielfache der Grundfrequenz auftreten. Wäre das nicht erfüllt, dann stimmt die Periodizität des Summensignals nicht mehr mit dem ursprünglichen Signal überein. Die niedrigste Frequenz, die als 1. Harmonische in der Originalfunktion vorkommt, ist durch ihre Periodendauer bestimmbar.
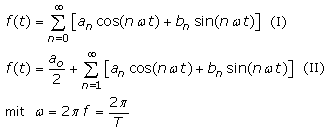
Bei bekannter Periodizität einer Funktion f(t) werden mit der Fourieranalyse die Fourier-Koeffizienten ao, an und bn bestimmt. Je mehr Koeffizienten bekannt sind, desto genauer kann die Funktion f(t) durch eine additive Überlagerung der dann bekannten harmonischen Teilschwingungen rekonstruiert werden. Dieser umgekehrte Vorgang ist die Fouriersynthese. Es ist wichtig, zwischen Sinus- und Cosinusgliedern zu unterscheiden. Ausschlaggebend ist der Startpunkt auf der Zeitachse. Wird sie auch ins Negative verlängert, dann ist zu erkennen, dass eine Cosinusfunktion achsensymmetrisch zur y-Achse verläuft und somit die Eigenschaft einer geraden Funktion hat. Die Sinusfunktion ist punktsymmetrisch zum Koordinatenursprung und hat die Eigenschaft einer ungeraden Funktion.
Bestimmung der Fourier-Koeffizienten
In der Fourierreihe nach (I) gibt es die Koeffizienten an und bn. Es sind die Amplituden für jede n-te Harmonische. In der Fourierreihe nach (II) steht vor dem Summenzeichen der Koeffizient ao. Er entspricht dem Gleichanteil des periodischen Originalsignals, wenn es zur Zeitachse nicht symmetrisch verläuft, also nach oben oder unten verschoben ist. Für jedes n kann die Fourierreihe durch ein entsprechendes Fourier Integral geschrieben werden. Integriert wird in den Grenzen einer Periodendauer T.


Wird die Fourierreihe mit der Sinusfunktion multipliziert, so hat in Analogie zur Herleitung oben das linke Teilintegral immer den Wert null. Die Fallbetrachtungen und Berechnungen erfolgen nur für das rechte Teilintegral. Ein dem a0 entsprechenden Faktor b0 gibt es nicht.

Mit den Teillösungen Gl.(1), Gl.(2) und Gl.(3) werden die Bestimmungsgleichungen mit den Laufzahlen n = m ≠0 und n = m = 0 für die Fourierkoeffizienten aufgestellt.
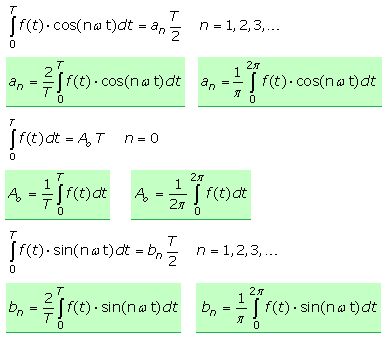
Die Formel zur Bestimmung von an gilt auch für die Laufzahl n = 0. Das Ergebnis ist ein Ausdruck für a0, mit dem doppelten Wert von A0. Am Anfang dieser Seite stehen mit Gl.(I) und Gl.(II) die beiden ähnlichen Funktionen für die trigonometrische Reihe. Soll nur eine Formel mit gleichem Berechnungsschema für alle Fourierkoeffizienten zur Anwendung kommen, dann erfolgt die Aufsummierung der Sinus-, Cosinusreihe von n = 1 ... ∞. Der Fourierkoeffizient a0 ist mit seinem halben Wert zu addieren.
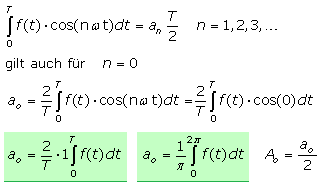
In europäischen Veröffentlichungen und Formelsammlungen sind Fourierreihen periodischer Funktionen mit Formeln zur Bestimmung der Fourierkoeffizienten zu finden.
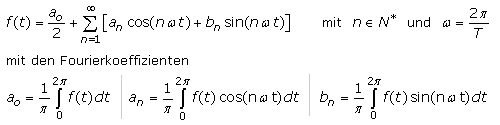
Schließt das Signal im Zeitintervall einer Periode oberhalb der Zeitachse die gleiche Fläche wie unterhalb der Zeitachse ein, so ist der Koeffizient a0 = 0. In der Elektrotechnik handelt es sich dann um ein zu null symmetrisches reines Wechselspannungs- oder Wechselstromsignal ohne Gleichanteil.
Nicht immer werden bei der Signalanalyse nach Fourier die Sinus- oder Cosinusfunktionen angegeben. Das Zeitdiagramm des Signals wird in ein Spektraldiagramm transformiert, das die Fourierkoeffizienten als Funktion der Ordnungszahl der auftretenden Harmonischen zeigt. Mithilfe dieser Fourier-Transformation (FT) kann die notwendige Bandbreite abgeschätzt werden, die zur Übertragung eines qualitativ gutes Signal gegeben sein muss. In den Spektraldiagrammen ist auch zu erkennen, ob und wie sich mehrere Signale, die gleichzeitig auf einem Kanal übertragen werden, gegenseitig beeinflussen.
Fourier-Transformation einfacher periodischer Signale
Das Frequenzspektrum eines Signals experimentell zu ermitteln ist prinzipiell nicht schwer. Die professionellen Messgeräte wie Spektrum-, Frequenzanalysator oder Klirrfaktormessbrücke benötigen eine komplizierte Elektronik und sind demzufolge teuer und stehen selten zur Verfügung. Wird das zu analysierende Signal an einen umschaltbaren und durchstimmbaren Parallelschwingkreis hoher Güte gelegt, dann können bei allen Harmonischen am Resonanzkreis Spannungsmaxima gemessen werden. Die Darstellung der Ausgangsamplituden als Funktion zu den ermittelten Resonanzfrequenzen ergibt das Frequenzspektrum. Die Höhe jeder Frequenzlinie entspricht dem Fourierkoeffizienten der jeweiligen Harmonischen.
Berechnung der Fourierkoeffizienten für ein Sinussignal
Die Fourier-Transformation wird nachfolgend am trivialen Beispiel eines reinen Sinussignals schrittweise durchgeführt. Die trigonometrische Reihe einer Sinusschwingung darf nur ganzzahlige Vielfache der Grundfrequenz enthalten. Die höheren Harmonischen müssen sich am Anfang und Ende jeder Periode gleichartig verhalten, um in der Summe die Periodizität des Signals nicht störend zu verändern. Für die Sinusfunktion der Amplitude y = 1 und der Frequenz ω werden die Fourierkoeffizienten hergeleitet. Die Sinuskurve umschließt innerhalb einer Periodendauer eine gleichgroße positive wie negative Fläche. Der erste Fourierkoeffizient sollte daher den Wert null haben. Die Sinusspannung ist ein reines Wechselspannungssignal ohne Gleichspannungsanteile.
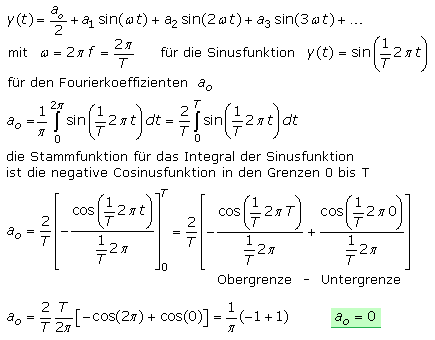
Die nächsten zu bestimmenden Fourierkoeffizienten sind an mit ganzzahligem n ≥1. Die Integration erfolgt immer über eine Periode. Integriert wird das Produkt der Funktion mit der Cosinusfunktion der n-fachen Frequenz. Da die Sinusfunktion unsymmetrisch zur y-Achse ist, treten keine Cosinuskomponenten auf und alle an Fourierkoeffizienten sollten null sein. Zum Beweis wird für den Koeffizienten a1 mit n = 1 wird die Berechnung ausführlich dargestellt. Die notwendigen Stammfunktionen sind in mathematischen Formelsammlungen zu finden. Für die höheren n muss die Zeitachse in Negative verlängert werden. Es ist zu erkennen, dass die Cosinuswerte für t = 0 und den Vielfachen der Periodendauer T immer den Wert 1 haben. Für das bestimmte Integral in den Grenzen 0 bis T ergibt die Stammfunktion in allgemeiner Berechnung für alle an folglich den Wert null.

Zur Bestimmung der Fourierkoeffizienten bn wird die Funktion mit ganzzahligen Vielfachen der Sinusfunktion multipliziert. Die Integration erfolgt wieder über eine volle Periode. Aus Erfahrung ist bekannt, dass nur eine Frequenzlinie auftreten kann, deren Höhe der maximalen Amplitude des Signals entspricht. Bei n = 1 ist die Stammfunktion für das Quadrat der Sinusfunktion zu verwenden. Für alle weiteren n stehen in Formelsammlungen ebenfalls die notwendigen Stammfunktionen. Es ist zu erkennen, dass die Klammerausdrücke (a + b) und (a − b) ganze Zahlen sind. Folglich haben für n > 1 die Sinuswerte an den Stellen t = 0 und den Vielfachen der Periodendauer T stets den Wert null. Das Frequenzspektrum der einfachen Sinusfunktion zeigt wie zu erwarten keine höheren Harmonischen, also keine Oberwellen sondern nur die Grundfrequenz als die 1. Harmonische mit der vorgegebenen maximalen Amplitude.

Fourier-Transformation eines Rechtecksignals
Mit Simulationsprogrammen für elektronische Schaltungen können unterschiedliche periodische Signale recht einfach auf ihren Oberwellenanteil hin untersucht werden. Die 1. Oberwelle oder Oberfrequenz ist die 2. Harmonische und hat die doppelte Frequenz der Grundwelle, der 1. Harmonischen. Wichtig ist dabei die korrekte Angabe der Analyseparameter, hier insbesondere der Periodendauer des Signals und die Zahl der zu ermittelnden Oberwellen. Die Programme können auch die Phasenlagen der Harmonischen zueinander analysieren. Das Simulationsprogramm EWB/Multisim gibt nicht immer verlässliche Werte aus und eine DC-Komponente wird nur im Tabellenwert angezeigt.
Die erste Analyse zeigt das Frequenzspektrum eines symmetrischen 1:1 Rechtecksignals. Die ersten Glieder der Fourierreihe stehen auch in Formelsammlungen. Das Spektrum ist normiert, wobei die Amplitude der 1. Harmonischen den Wert 1 hat. Das Tastverhältnis beträgt V = 2 und somit fehlt jede 2. Harmonische. Das Signal hat keine DC-Komponente, da während einer Periode die Flächensumme im Positiven und Negativen gleich ist und sich zu null ausgleicht.
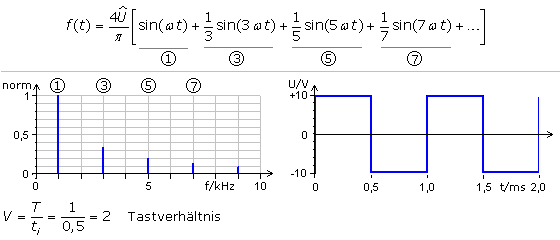
Das im Bild rechts dargestellte Zeitdiagramm des Rechtecksignals soll nun mathematisch durch die Fourier-Transformation in das Spektrum überführt werden. Das Signal ist zur y-Achse unsymmetrisch, also werden alle Fourierkoeffizienten an = 0 sein. Es ist zur Zeitachse symmetrisch und umschließt während einer Periode gleichgroße positive wie negative Flächeneinheiten. Das Rechteck hat keine DC-Komponente und der erste Fourierkoeffizient sollte ao = 0 betragen. Das Signal hat bei der halben Periode eine Sprungstelle. Für den Bereich 0 bis T/2 oder π (Pi) entspricht der Signalverlauf einer positiven Konstanten und danach von T/2 bis T einer negativen Konstanten. Zur Bestimmung der Fourierkoeffizienten ist über die gesamte Periode zu integrieren.

Die Fourierkoeffizienten an haben für alle n den Wert null. Die Integration erfolgt für die Produkte der Teilfunktionen mit den Cosinusfunktionen aller ganzzahligen Vielfachen der Periode. Die Stammfunktion eines Cosinusintegrals ist eine Sinusfunktion die an den Integrationsgrenzen 0, T/2 und T und deren ganzzahligen Vielfachen immer null ergibt. Zu ermitteln bleiben die Fourierkoeffizienten bn für die Produkte der Teilfunktionen mit den Sinusfunktionen und deren ganzzahligen Vielfachen der Grundfrequenz. Die Stammfunktion ist in mathematischen Formelsammlungen zu finden.
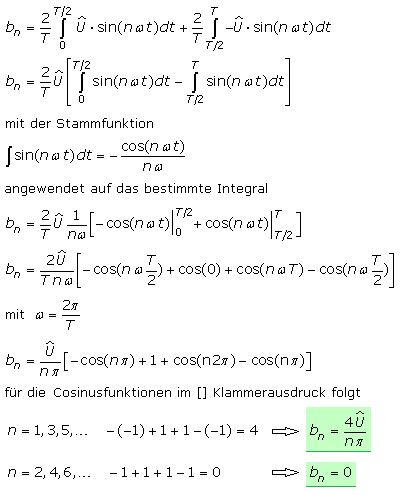
Die Berechnungen zeigen, dass im Frequenzspektrum des symmetrischen Rechecksignals nur alle ungeraden Harmonischen vorkommen, so wie es das Simulationsergebnis darstellt. Es folgt die Berechnung der Amplituden der auftretenden Harmonischen, die aus der allgemeinen Formel für bn erkennbar, mit zunehmender Frequenz kontinuierlich abnehmen. Sowohl die Formelsammlungen als auch das Simulationsprogramm notiert die Amplituden als normierte Werte bezogen auf die Amplitude der Grundfrequenz.
| n | 1 | 3 | 5 | 7 | 9 |
| bn | 1,273 | 0,424 | 0,255 | 0,182 | 0,141 |
| normiert | 1 | 0,333 = 1/3 | 0,200 = 1/5 | 0,143 = 1/7 | 0,111 = 1/9 |
Fourier-Transformation eines Sägezahnsignals
Im Simulationsprogramm wurde zur Frequenzanalyse das Tastverhältnis V = 1 eingestellt, sodass bei jeder 100. Harmonische eine Nullstelle auftritt. Dieses Sägezahnsignal entspricht im Bereich einer Periode idealisiert der Funktion einer Geraden mit negativer Steigung (blauer Kurvenzug). Ein Sägezahn mit V = 99 kann idealisiert durch die gleiche Gerade mit positiver Steigung (grün) dargestellt werden. Die Simulation liefert für beide ein identisches Frequenzspektrum. Mathematisch ändert sich nur das Vorzeichen für die Fourierkoeffizienten bn.
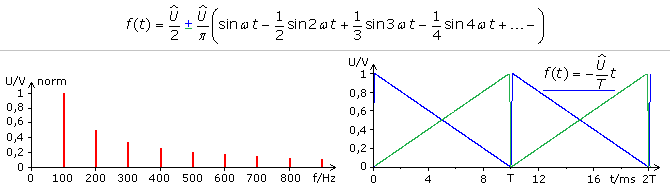
Der Signalverlauf ist zur Amplitudenachse unsymmetrisch, es treten daher keine Cosinusfunktionen mit den Fourierfaktoren an auf. Berechnet werden müssen die Integrale für ao und bn aus dem Produkt der Funktion mit der Sinusfunktion für n ≥ 1.
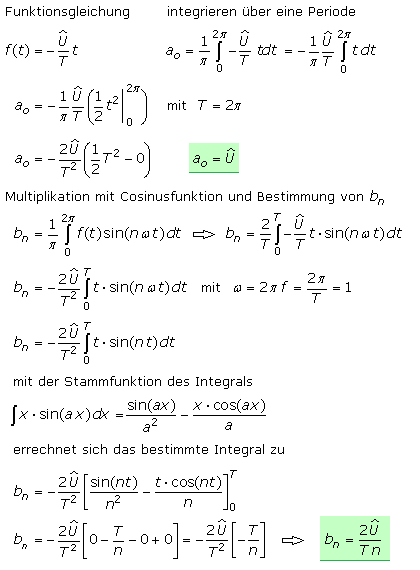
Das Signal verläuft nur im Positiven und hat somit eine DC-Komponente. Sie entspricht dem Flächeninhalt, den die Kurve mit der Zeitachse einschließt. Es ist die halbe Rechteckfläche, als Produkt der maximalen Spannung mit der Periodendauer bezogen auf eine Periode und damit identisch mit dem Fourierfaktor ao/2. Die Tabelle zeigt die Fourierfaktoren der ersten 7 Frequenzlinien und deren normierte Werte.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| bn | 0,3183 | 0,1592 | 0,1061 | 0,0796 | 0,0637 | 0,0531 | 0,0455 |
| normiert | 1 | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/7 |
In der animierten Fouriersynthese verlaufen die Sägezahnsignale symmetrisch zur Zeitachse, wobei es zum kontinuierlichen Vorzeichenwechsel bei den Koeffizienten kommen kann. Diese Signale haben entweder eine Sprungstelle bei der halben Periode oder kreuzen die Zeitachse. In beiden Fällen wechselt das Vorzeichen der Amplitude. Das Frequenzspektrum ändert sich nicht, da alle Linien nach Vereinbarung im Positiven dargestellt werden. Die Integration zur Berechnung der Fourierkoeffizienten muss als Summe der Teilintegrale von 0 bis T/2 und T/2 bis T mit der dazu passenden Funktionsgleichung durchgeführt werden.
Fourier-Transformation eines periodischen Rechteckpuls
Die Fourieranalyse eines Rechtecksignals mit dem Tastverhältnis V = 5 bei gleich großen positiven wie negativen Amplituden zeigt im Spektrum das Fehlen jeder 5. Harmonischen. Die Flächenverteilung über eine Periode lässt eine DC-Komponente erwarten, die im Simulationsergebnis nur tabellarisch angezeigt wird. Da das Signal weder symmetrisch noch unsymmetrisch ist, #treten bei der Fourier-Transformation beide Koeffizienten an und bn auf. Das im Simulationsprogramm zur Zeitachse symmetrische Signal hat die Grundfrequenz 100 Hz und die Spannung U = 10 V.
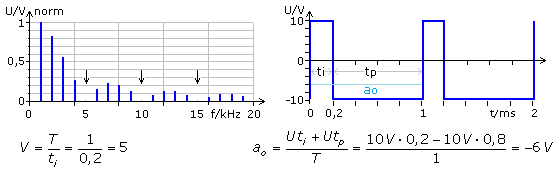
Bei der Berechnung der Fourierkoeffizienten ist über eine Periodendauer T zu integrieren, wobei die Summe der Teilintegrale für die Funktion f(t) = +U in den Grenzen 0 bis T/5 und f(t) = −U in den Grenzen T/5 bis T zu bilden ist. Die Bestimmung der DC-Komponente kann ebenso einfach auch ohne Integration als Mittelwert nach der angegeben Formel errechnet werden.

Beide Fourierkoeffizienten an und bn haben bei den Vielfachen von n = 5 den Wert null. Im Frequenzspektrum fehlt, so wie es das Simulationsergebnis zeigt, jede 5. Harmonische. Mit den Koeffizienten kann die Fourierreihe für den periodischen Recheckpuls geschrieben werden. Die Amplituden der Harmonischen lassen sich noch nicht wie in den vorangegangenen Beispielen direkt mit den Koeffizienten vergleichen. In der trigonometrischen Reihe wird an mit der Cosinusfunktion und bn mit der Sinusfunktion multipliziert und die Summe gebildet. In umfangreichen Formelsammlungen findet man eine vereinfachende Lösung.

In der Tabelle sind die Amplituden der ersten 10 Harmonischen berechnet und stimmen mit den Ergebnissen der Simulation überein. Der aus dem Arcustangens folgende Phasenwinkel beträgt für dieses Beispiel 36° und ist der halbe Wert, der sich aus dem Winkelverhältnis φ1 = ti / T = 72° ergibt.
| n | an | bn | √(an2+bn2) | normiert |
| 1 | 0,6055 | 0,4399 | 0,7484 | 1 |
| 2 | 0,1871 | 0,5758 | 0,6054 | 0,8100 |
| 3 | -0,1247 | 0,3839 | 0,4036 | 0,5393 |
| 4 | -0,1514 | 0,1100 | 0,1871 | 0,2501 |
| 5 | 0 | 0 | 0 | 0 |
| 6 | 0,1009 | 0,0733 | 0,1247 | 0,1666 |
| 7 | 0,0535 | 0,1645 | 0,1730 | 0,2311 |
| 8 | -0,0468 | 0,1440 | 0,1514 | 0,2023 |
| 9 | -0,0673 | 0,0489 | 0,0832 | 0,1112 |
| 10 | 0 | 0 | 0 | 0 |