Die Gerade – Polynomfunktion 1. Grades

Im der praktischen Elektrophysik wird beispielsweise die Abhängigkeit von Spannung und Strom an Baugruppen untersucht. Sind die Messungen von mehreren Parametern abhängig, so sollte bei den Messungen immer nur ein Parameter variiert werden, um seinen Einfluss auf die zu bestimmende Messgröße zu erkennen. Die Auswertung kann rein mathematisch und auch mithilfe einer grafischen Darstellung im rechtwinkligen Achsenkreuz durchgeführt werden. Unter Berücksichtigung der stets auftretenden Messungenauigkeiten liegen für einen gewählten ohmschen Widerstand alle Messpunkte für die Abhängigkeit zwischen angelegter Spannung und dem resultierenden Strom auf einer Ausgleichsgeraden. Die kürzeste Verbindung zwischen zwei Punkten in der Ebene wird als Gerade bezeichnet.

Bei der grafischen Darstellung des Widerstandsversuchs werden die frei wählbare Spannungswerte auf der horizontalen Achse, der mathematischen x-Achse, abgetragen. Die sich einstellenden Stromwerte werden auf der dazu senkrecht stehenden Achse, der mathematischen y-Achse, eingezeichnet. Für einen bestimmten Widerstand ergeben sich die Ströme als Funktionswerte der angelegten Spannungen. Der durch den Widerstand fließende Strom ist eine Funktion der am Widerstand anliegenden Spannung. Das Funktionsbild ist in den meisten Fällen eine Gerade und zeigt den linearen, proportionalen Zusammenhang zwischen Strom und Spannung.

Aus der praktischen Messreihe kann eine theoretische mathematische Gesetzmäßigkeiten hergeleitet werden. Bestätigen viele voneinander unabhängig durchgeführte Versuche diese Gesetzmäßigkeit, dann ist sie solange allgemeingültig, bis reproduzierbare Versuche andere Ergebnissen liefern. Durch Hinzufügen neuer erkannter Versuchsparameter kann diese erste Gesetzmäßigkeit erweitert und spezifiziert werden. Die Elektronik ist ein Teilbereich der Naturwissenschaften und die Mathematik ist die Beschreibungssprache als Verbindung zwischen Praxis und Theorie.

Die Achsenabschnittsform einer Geraden

Sind im ebenen rechtwinkligen Achsenkreuz die beiden Achsenabschnitte a und b bekannt, dann liegt der Punkt A(a; 0) auf der x-Achse und B(0; b) auf der y-Achse. Es lassen sich verschiedene Trennzeichen zwischen den Koordinatenwerten eines Punktes finden. Das Semikolon (;) oder der senkrechte Strich (|) sind kaum verwechselbar. Ein Komma (,) sollte nicht verwendet werden, wenn es mit dem Dezimaltrennzeichen verwechselt werden kann. Die Punkte A und B werden Spurpunkte genannt. Die kürzeste Verbindung zwischen ihnen ist die Spurgerade. Jeder andere Punkt P auf dieser Geraden mit den Koordinaten P(x; y) erfüllt immer dann die Achsenabschnittsform, wenn a≠0 und b≠0 ist. Da es sich um eine Geradengleichung handeln soll, treten x und y in den Termen nur linear auf, sind also in der 1. Potenz enthalten und additiv miteinander verknüpft. In der Physik haben die Achsenabschnitte oft unterschiedliche Einheiten. Soll das Ergebnis ein reiner Zahlenwert sein, wird der zugehörige Achsenabschnittswert durch seine Einheit dividiert. Aus der Achsenabschnittsform kann die Funktionsgleichung der Geraden hergeleitet werden.

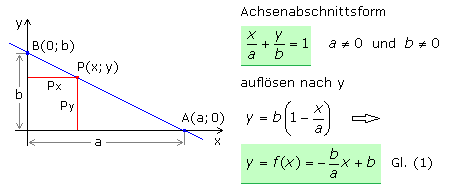
Die Achsenabschnittsform nach y aufgelöst ergibt die lineare Funktion Gl.(1). Für x = 0 errechnet sich der Spurpunkt B(0; b) und für y = 0 der Spurpunkt A(a; 0). Mithilfe der Achsenabschnittsform können Geradengleichungen nur dann ermittelt werden, wenn es zwei von null verschiedene Achsenabschnitte gibt. Die Gerade darf nicht durch den Koordinatenursprung verlaufen. Der Koeffizient (Multiplikationsfaktor) vor x entspricht der Geradensteigung und ist das Verhältnis der Achsenabschnitte (b / a). Der Schnittpunkt der Gerade mit der y-Achse wird als absolutes Glied der Geradengleichung bezeichnet und ist gleich dem Achsenabschnitt b.

Die Zweipunkteform einer Geraden

Die kürzeste Verbindung zwischen zwei Punkten P1 und P2 ist eine Gerade. Mit den Koordinaten dieser Punkte kann die Funktionsgleichung der Geraden eindeutig hergeleitet werden. Jeder beliebige Punkt P(x; y) auf dieser Geraden ist zu den gegebenen beiden Punkten ebenfalls linear und muss die Funktionsgleichung erfüllen. Nach dem Strahlensatz der Geometrie sind die Streckenverhältnisse jedes Punktepaares zueinander gleich.

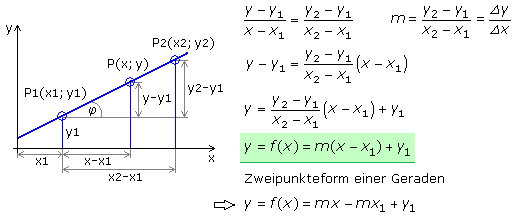
Die Funktion f(x) ist die nach y umgeformte Zweipunktegleichung, mit der für jeden gewählten x-Wert der davon abhängige y-Wert errechnet werden kann. Die allgemeine Funktionsgleichung einer Geraden besteht aus einem linearen Glied mit x in der 1. Potenz und einem absoluten Glied ohne x. Der Koeffizient von x gibt die Steigung der Geraden in Bezug zur x-Achse und das absolute Glied den Schnittpunkt mit der y-Achse an.

Die Normalform einer Geraden

Die allgemeine mathematische Schreibweise einer Geradengleichung ist y = f(x) = m·x + n, wobei m und n reelle Zahlen sind. Der Faktor m steht für die Steigung der Geraden und n ist der Schnittpunkt mit der y-Achse, wenn x = 0 gesetzt wird. Mit n = 0 verläuft die Gerade durch den Koordinatenursprung und wird als Ursprungsgerade bezeichnet. Die Geradenfunktion ist für alle reellen x-Werte definiert.

Eine mathematische Funktion ist definiert als eindeutige Zuordnung der Werte aus einer Definitionsmenge zur Ergebnis-(Werte)-Menge. Für jeden x-Wert kann es nur einen y-Wert geben.

Für eine parallel zur y-Achse verlaufenden Geraden ist keine Funktionsgleichung definiert, da dem einzigen x-Wert viele y-Werte zugeordnet sind. Für eine parallel zur x-Achse verlaufende Gerade ist die Bedingung für eine Funktionsgleichung erfüllt. Der Steigungsfaktor ist null, der Funktionswert ist für alle x konstant.

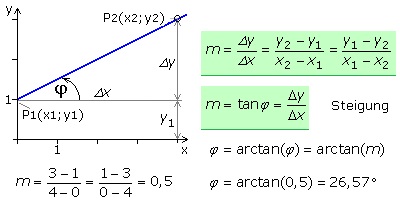
Die Steigung einer Geraden

In der Geradenfunktion ist die Steigung m der Koeffizient des linearen Glieds und berechnet sich aus dem Differenzenquotienten, dem Verhältnis des y-Abschnitts zum x-Abschnitt zwischen zwei gewählten Punkten der Geraden. Die Steigung ist somit die auf die Horizontale bezogene Neigung der Geraden und kann durch den Steigungswinkel φ mit der Horizontalen angegeben werden. Der Winkelwert nimmt gegen den Uhrzeigersinn linksdrehend zu. Die Steigung m errechnet sich im rechtwinkligen Steigungsdreieck aus dem Quotienten der Gegenkathete Δy zur Ankathete Δx. Zur Berechnung der Steigung ist es egal, ob die Koordinaten P1 von P2 oder umgekehrt subtrahiert werden. Wichtig ist nur die gleiche Reihenfolge der Indizes im Zähler und Nenner. Steigungswinkel von φ = 90° oder ganzzahligen Vielfachen davon widersprechen der Definition der Funktion.

Orthogonale Geraden

Sollen sich in der Ebene zwei Geraden rechtwinklig schneiden und ist die Steigung m der einen Geraden bekannt, dann hat die andere Gerade den Steigungsfaktor −1/m, also den negativen Kehrwert des gegebenen Steigungsfaktors. Um aus dem benennungslosen Zahlenwert der Steigung den Steigungswinkel im Gradmaß anzugeben, muss für den tan(φ) die Umkehrfunktion arctan(φ) = φ verwendet werden. Für eine Geradenfunktion mit m = 0 kann keine orthogonale Geradenfunktion geschrieben werden, da die Division durch null nicht definiert ist.

Die Punktsteigungsform einer Geraden

Jede Gerade, die nicht parallel zur y-Achse verläuft, ist durch einen auf ihr liegenden Punkt P(x1; y1) und ihre Steigung m = Δy / Δx eindeutig bestimmbar. Die Herleitung erfolgt mit der Normalform und einer zweiten Gleichung, wo die Punktkoordinaten in die Normalform eingesetzt sind. Beide Gleichungen werden voneinander subtrahiert und nach y umgestellt. Das Ergebnis ist identisch mit der Funktionsgleichung, die als Zweipunkteform hergeleitet wurde.

Herleitung für m und n mithilfe der Normalform einer Geraden

Die Koordinaten zweier Punkte, die auf einer Geraden liegen, erfüllen die Gleichung Normalform. Beim Einsetzen der Punktkoordinaten in die Normalform ergeben sich zwei Gleichungen. Sie sind für die beiden Unbekannten m und n lösbar. In den folgenden Herleitungen werden sie aus den Ausgangsgleichungen allgemein bestimmt. Es kann auch entweder m oder n hergeleitet und das Ergebnis in eine der beiden Ausgangsgleichungen einsetzt und so die zweite Unbekannte ermittelt werden.

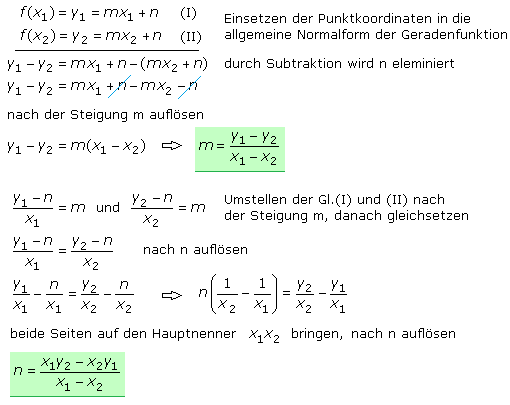
Wird der Ausdruck für das absolute Glied aus der Zweipunkteform ausgerechnet und umgeformt, so ist das Ergebnis identisch mit dem Term für das hier hergeleitete absolute Glied n.

Hessesche Normalform – HNF

Mithilfe der HNF kann relativ einfach der direkte Abstand eines Punktes oberhalb oder unterhalb einer Geraden bestimmt werden. Auch in der Vektorgeometrie hat die HNF einen besonderen Platz. Der kürzeste Abstand zwischen einer Geraden und dem Koordinatenursprung ist eine auf ihr senkrecht stehende Gerade, die Normale. Sie bildet mit der x-Achse einen Winkel φ. Sind die Länge der Normalen p und der Winkel bekannt, kann die Hessesche Normalform wie folgt geschrieben werden:
x·cos(φ) + y·sin(φ) = p. Mit dem Winkel φ sind die Punktkoordinaten auf der Geraden und die Geradensteigung bekannt. Mit der Punkt-Steigungs-Form kann die HNF aufgestellt werden.

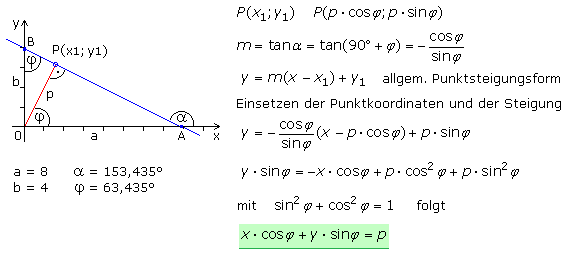
Die Gerade ist eindeutig bestimmbar, wenn die Länge der Normalen p bekannt ist. Die allgemeine Form der Geradengleichung A·x + B·y + C = 0 kann in die Hessesche Normalform umgewandelt werden. Die linke Seite ist durch die Wurzel aus der Summe der Quadrate von A und B zu dividieren. Nur für das neue absolute Glied p muss das Vorzeichen der Wurzel entgegengesetzt zum Vorzeichen des absoluten Glieds C sein. Das absolute Glied dividiert durch den Wurzelausdruck gibt die Länge der Normalen als kürzesten Abstand der Geraden zum Koordinatenursprung an. Diese Strecke steht senkrecht auf der Geraden.

Mithilfe der zugehörigen Grafik oben zeigen sich die Übereinstimmungen zwischen der allgemeinen Form der Geradengleichung und ihrer daraus herzuleitenden HNF. Die Geradengleichung in allgemeiner Form lautet: 0,5·x + y − 4 = 0, und als Hessesche Normalform: x·cos(φ) + y·sin(φ) + 3,578 = 0