Matrizen in der Mathematik
In der erweiterten Mathematik linearer Gleichungssysteme und in der Elektronik wo besonders mit Zweitordarstellungen bei Filterschaltungen gerechnet werden soll, werden Parameter und Funktionen in einer besonderen Schreibweise, der Matrix dargestellt. Der Begriff kommt aus dem Lateinischen und steht für ein Verzeichnis als strukturierte Anordnung von Daten, in der Biologie bezeichnet sie eine Gebärmutter oder Keimschicht. Im Plural sind es die Matrizen.
Die Matrix ist ein rechteckiges System mit (m * n) Plätzen, wo die Komponenten oder Elemente in m Zeilen und n Spalten angeordnet sind. Jeder Eintrag hat seinen definierten Platzindex (i,k). Die Matrix wird mit einem Großbuchstaben bezeichnet und der Komponentenblock insgesamt in runde Klammern gesetzt. Die Komponenten erhalten allgemein geschrieben den Kleinbuchstaben des Matrixbezeichners mit dem Zeilen- und Spaltenindex. Das Bild zeigt die allgemeine Darstellung einer Matrix.
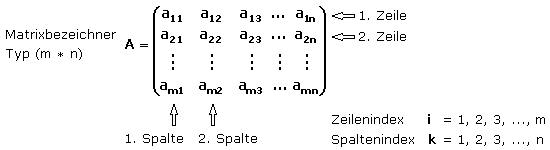
Die in einer Matrix A indizierte Komponente ai,k steht in der i-ten Zeile und k-ten Spalte und ist somit eindeutig bezeichnet. Eine Matrix mit m Zeilen und n Spalten ist vom Typ (m * n), wobei die Zeilen auch als Zeilenvektor und die Spalten als Spaltenvektor der Matrix bezeichnet werden.
- Zeilenmatrix
- Sie besteht aus nur einer Zeile und ist vom Typ (1 * n) und somit ein Zeilenvektor.
- Spaltenmatrix
- Sie besteht aus nur einer Spalte und ist vom Typ (m * 1) und somit ein Spaltenvektor.
- Skalar
- Er ist eine Matrix vom Typ (1 * 1) mit gleichem Zeilen- und Spaltenvektor.
Quadratische Matrix
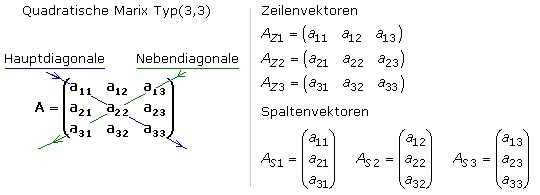
Eine Matrix mit der gleichen Anzahl Zeilen und Spalten ist vom Typ (m * m) und hat als einzige Matrix eine Haupt- und Nebendiagonale. Die Hauptdiagonale verläuft vom Eintrag a11 links oben und endet rechts unten mit dem Eintrag amm. Einen vergleichbaren Verlauf hat die Nebendiagonale von rechts oben nach links unten. Sie beinhaltet die Komponenten a1m und am1. Das Bild zeigt die allgemeine Nomenklatur einer quadratischen Matrix (3,3) und die Schreibweise ihre Zeilen- und Spaltenvektoren.
Transponierte Matrix
Werden bei einer Matrix A vom Typ (m * n) die Zeilen in eine neue Matrix als Spalte geschrieben, so erhält man die transponierte Matrix AT vom Typ (n * m). Die Komponenten der Matrix und ihrer transponierten Matrix stehen einander zu ai,k = aTk,i. Durch zweimaliges Transponieren erhält man wieder die Ausgangsmatrix. Eine quadratische Matrix transponiert entspricht der Spiegelung ihrer Komponenten an der Hauptdiagonalen.
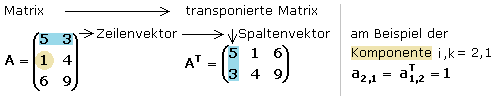
Diagonalmatrix und Einheitsmatrix
Es handelt sich dabei stets um eine quadratische Matrix. Bei der Diagonalmatrix hat nur die Hauptdiagonale Werte die ungleich 0 sind. Alle anderen Komponenten haben den Wert 0. Die Einheitsmatrix ist der Spezialfall einer Diagonalmatrix, bei der alle Hauptdiagonalelemente den Wert 1 und alle anderen den Wert 0 haben.
Rechenoperationen mit Matrizen
Für Matrizen gibt es diverse Rechenoperationen, von denen nur einige hier kurz vorgestellt werden. Das Ergebnis ist eine neue Matrix.
Addition zweier Matrizen
Die Addition ist für Matrizen gleichen Typs definiert. Bei der Addition werden nur die Komponenten mit gleichen Indizes addiert. Es gilt das Kommutativgesetz mit A + B = B + A und das Assoziativgesetz mit A + (B + C) = (A + B) + C. Das Bild veranschaulicht das Additionsverfahren.

Subtraktion zweier Matrizen
Nur Matrizen des gleichen Typs dürfen subtrahiert werden, wobei die Komponenten mit gleichen Indizes voneinander abgezogen werden. Es gilt weder das Kommutativ- noch das Assoziativgesetz. Das folgende Bild zeigt das allgemeine Verfahren und ein Zahlenbeispiel.

Multiplikation mit einem Skalar
Eine Matrix kann mit einer skalaren Größe, einer Zahl multipliziert werden, wobei jede Komponente mit dem Skalar multipliziert wird. Das bedeutet auch, falls in allen Komponenten einer Matrix der gleiche skalare Wert vorkommt, so kann er vor die Matrix gesetzt werden. Es gilt das Assoziativgesetz und das Distributivgesetz.

Multiplikation zweier Matrizen
Das Produkt der Matrix A mit der Matrix B ergibt nur dann die Ergebnismatrix C, wenn die Spaltenzahl der Matrix A mit der Zeilenzahl der Matrix B übereinstimmt. Es muss also Matrix A vom Typ (m,n) und Matrix B vom Typ (n,p) erfüllt sein, da bei der Matrixmultiplikation das skalare Produkt nur zwischen Vektoren mit gleicher Komponentenzahl definiert ist. Die Ergebnismatrix hat dann so viele Zeilen wie die Matrix A und Spalten wie die Matrix B. Bei der Multiplikation werden die Komponenten als Skalarprodukte des i-ten Zeilenvektors der Matrix A mit dem k-ten Spaltenvektor der Matrix B erstellt. Die Matrizenmultiplikation erlaubt das Assoziativgesetz und das Distributivgesetz, während das Kommutativgesetz bis auf wenige Ausnahmen nicht gilt.

Das Falk-Schema vereinfacht die manuelle Multiplikation von Matrizen. Die zu multiplizierenden Matrizen werden rechtwinklig zueinander verschoben, sodass die Zeilen der Matrix A unterhalb und links neben den Spalten der Matrix B zu liegen kommen. Die Kreuzungspunkte Zeile A * Spalte B errechnen sich dann leicht überschaubar aus den Skalarprodukten des Zeilenvektors von A mit dem Spaltenvektor von B. Der Videoclip zeigt das Falk-Schema.