Winkelfunktionen im rechtwinkligen Dreieck
In der Wechselstrom- und Nachrichtentechnik werden Signale mathematisch oftmals durch Winkelfunktionen beschrieben. Die Wechselstromkurve mit sinusförmigem Verlauf entsteht bei der Rotation einer Leiterschleife in einem homogenen Magnetfeld. Die Berechnung von Wechselstromgrößen gemischter Schaltungen ist nur mit Winkelfunktionen möglich. Werden Zeiger oder die komplexe Zahlenebene benutzt, so sind auch dort die Winkelfunktionen ein fester Bestandteil.
Der Teil der Mathematik, der die Berechnung ebener Dreiecke mithilfe von Winkelfunktionen durchführt, wird Trigonometrie genannt. Die Grundlage aller Berechnungen ist dabei das rechtwinklige Dreieck. Die schiefwinkligen Dreiecke lassen sich durch das Fällen einer Höhe in zwei rechtwinklige Dreiecke zerlegen. Alle Winkelfunktionen haben keinen algebraischen Charakter und werden als transzendente Funktionen bezeichnet. Diese Seite umfasst nach den Winkelfunktionen des rechtwinkligen Dreiecks folgende Thematik:
- Beziehungen zwischen den Funktionen desselben Winkels
- Additionstheoreme – Funktionen zusammengesetzter Winkel
- Trigonometrische Funktionen des doppelten Winkels
- Summen und Differenzen einiger Winkelfunktionen
- Die Produkte einiger Winkelfunktionen
- Funktionsreihen
Zwei rechtwinklige Dreiecke, die in einem ihrer spitzen Winkel übereinstimmen, sind einander ähnlich. Das Verhältnis zweier entsprechender Seiten ist konstant und nur vom Winkel abhängig, es ist also eine Winkelfunktion. Die beiden kürzeren Seiten a und b sind die Katheten und die längere Seite c ist die Hypotenuse. Der Schenkel, der dem Winkel α anliegt, ist die Ankathete. Die Kathete b liegt diesem Winkel gegenüber und wird als Gegenkathete bezeichnet. Die Winkelschenkel ins Verhältnis gebracht führt zu den Winkelfunktionen, die im Beispiel für den Winkel α aufgestellt sind. Die Cosinus- und Cotangensfunktion beginnt mit 'co' einer lateinischen Vorsilbe in der Bedeutung 'mit' oder 'zusammen'. Ein Hilfsmittel beim Aufstellen der Winkelfunktion, wo das Verhältnis dann mit der am Winkel anliegenden Kathete beginnt.
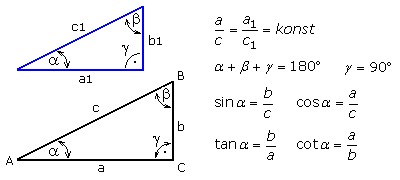
Um Funktionen im rechtwinkligen Achsenkreuz darzustellen, geht man vom Einheitskreis mit der Länge des Radius r = 1 hat. Der nach rechts weisende waagerechte Radius, die mathematische x-Achse, ist als Bezugs- oder Nullrichtung definiert. Für die Sinus- und Cosinusfunktion dreht man diesen Radius entgegen dem Uhrzeigersinn um einen Winkel φ. Für jeden Drehwinkel erhält man einen Punkt P auf der Kreislinie. Das Lot von diesem Punkt auf die Nullrichtung ist die Gegenkathete b zum Drehwinkel. Die Projektion des gedrehten Radius auf die Nullrichtung ist die Ankathete a des Winkels. Da der Radius als Hypotenuse festgelegt die Länge 1 hat, ist die Maßzahl der Gegenkathete gleich dem Sinus des Winkels und die Maßzahl der Ankathete gleich dem Cosinus dieses Winkels. Die Maßzahlen werden auf der y-Achse des Koordinatensystems abgetragen. Die Teilung der x-Achse kann im Winkelmaß oder im Bogenmaß erfolgen, wobei 2·π = 360° entsprechen.
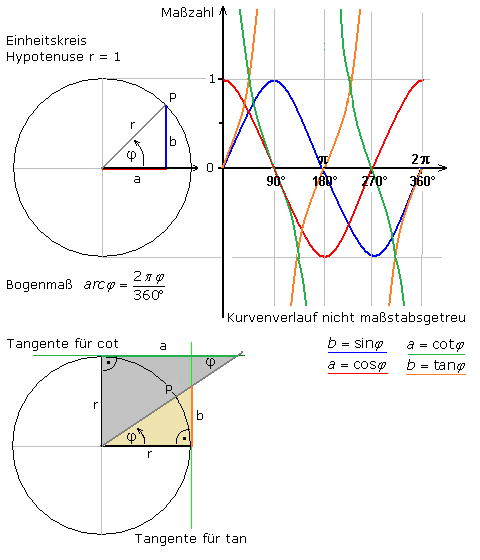
Zur Konstruktion der Tangensfunktion aus dem Einheitskreis zeichnet man im Endpunkt des Radius in seiner Nullrichtung die Tangente an den Kreis. Der Radius wird um den Winkel φ aus der Nullrichtung entgegen dem Uhrzeigersinn gedreht. Der gedrehte Radius wird über den Punkt P hinaus bis zum Schnittpunkt mit der Tangente verlängert. Im gelben rechtwinkligen Dreieck ist der dabei entstandene Tangentenabschnitt b die Gegenkathete zum Drehwinkel. Da der Radius in Nullrichtung als Ankathete die Länge 1 hat, entspricht die Maßzahl des Tangentenabschnitts dem Tangens des Winkels.
Zur Konstruktion der Cotangensfunktion wird parallel zur Nullrichtung die Tangente an den Einheitskreis gelegt. Der um den Winkel φ gedrehte Radius wird über P hinaus bis zum Schnittpunkt mit dieser Tangente verlängert. Im grauen rechtwinkligen Dreieck ist der Tangentenabschnitt a die Ankathete zum Drehwinkel, während der zur Nullrichtung senkrecht stehende Radius die Gegenkathete mit der Länge 1 ist. Damit entspricht die Maßzahl dieses Tangentenabschnitts dem Cotangens des Winkels.
Werden diese Operationen für alle Winkel von 0° ... 360° vorgenommen, so ergeben sich die Kurvenzüge der vier wichtigen Winkelfunktionen. Da bei ähnlichen Dreiecken immer das Verhältnis zweier entsprechender Strecken gleich ist, kann die Tangens- und Cotangensfunktion auch aus einem Verhältnis der Sinus- und Cosinusfunktion hergeleitet werden.
tanφ = sinφ / cosφ und entsprechend gilt: cotφ = cosφ / sinφ
Für Winkelwerte von 0° bis 90° ist das Ergebnis der Winkelfunktionen immer positiv. Werden alle Winkel des Vollkreises durchlaufen, so können sich die Vorzeichen für den jeweiligen Quadranten ändern. Nach 360° ist eine volle Periode durchlaufen und der Vorgang wiederholt sich. Winkelfunktionen beliebig großer Winkel berechnen sich aus dem Restwinkelwert, der nach Abzug eines ganzzahligen Vielfachen von 360° bleibt.
| Qu. | Winkelbereich | Sinus | Cosinus | Tangens | Cotangens |
| I. | 0° ... 90° | pos | pos | pos | pos |
| II. | >90° ... 180° | pos | neg | neg | neg |
| III. | >180° ... 270° | neg | neg | pos | pos |
| IV. | >270° ... 360° | neg | pos | neg | neg |
Der Komplementwinkel
In jedem Dreieck beträgt die Winkelsumme 180°. Im rechtwinkligen Dreieck hat einer immer den Wert 90°. Zieht man von einem der beiden Dreieckswinkel den rechten Winkel ab, so erhält man den seinen Komplementwinkel. Wechselt man von einem Winkel zum Komplementwinkel, so muss man bei der Winkelfunktion zur Cofunktion des Winkels wechseln. Die Namen Cosinus und Cotangens leiten sich von
'complementi sinus (tangens)' ab.
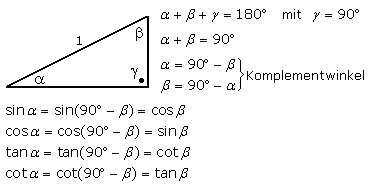
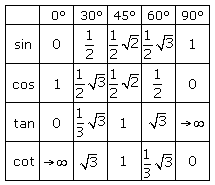
Einfach zu merkende Funktionswerte
Zum schnellen Zeichnen des Kurvenverlaufs der Winkelfunktionen sind die nebenstehenden fünf Funktionsergebnisse hilfreich. Sie leiten sich aus einem gleichschenklig, rechtwinkligen Dreieck für den Winkel von 45° sowie aus einem gleichseitigen Dreieck für die Winkel 30° und 60° her. Dazu kommen noch die Werte für die Winkel 0° und 90°. Die Herleitung der Ergebnisse ist aus der folgenden Skizze ersichtlich.
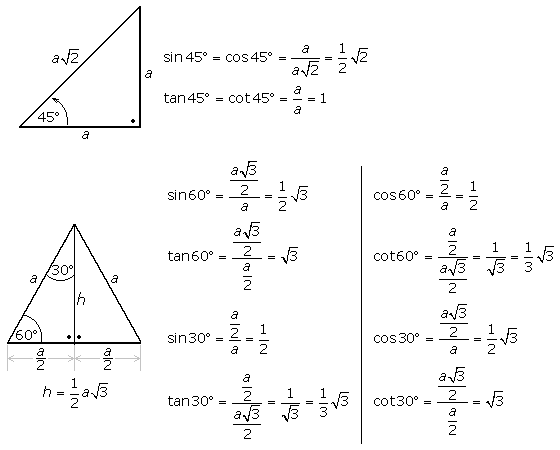 △
△
Beziehungen zwischen den Funktionen desselben Winkels
Hat die Hypotenuse eines rechtwinkligen Dreiecks die Längeneinheit 1, so lassen sich die Kathetenlängen durch die Maßzahlen des Winkels ersetzen. Der Satz des Pythagoras kann dann für die Sinus- und Cosinusfunktion in der nachstehenden Form geschrieben werden. Mit den weiter oben gezeigten Verhältnissen für die Tangens- und Cotangensfunktion leiten sich die anderen Beziehungen zwischen den Winkelfunktionen her.
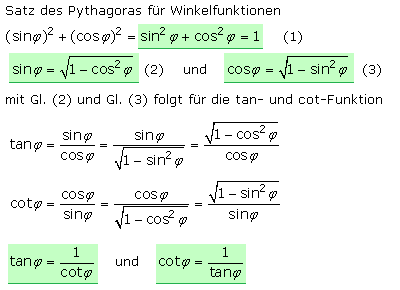
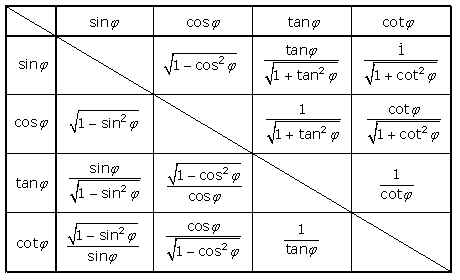
Diese Winkelbeziehungen lassen sich übersichtlich darstellen. Bei Winkelwerten über 90° sind die Vorzeichen der Winkelfunktionen für die einzelnen Quadranten zu beachten.
 △
△
Additionstheoreme – Funktionen zusammengesetzter Winkel
In der Nachrichtentechnik setzen sich die Signale aus vielen sinusförmigen Schwingungen unterschiedlicher Frequenzen und Amplituden zusammen, die zueinander noch phasenverschoben sein können. Die Einzelsignale überlagern sich additiv oder subtraktiv zum Gesamtsignal. Das Ergebnis kann ein Schwebungston, Musik oder Sprache sein. Bei der multiplikativen Überlagerung einzelner Signale bilden sich Modulationsprodukte mit ganz anderen Eigenschaften. Zur mathematischen Herleitung dieser Vorgänge benötigt man zur Zusammenfassung und Umstellung der Funktionsgleichungen die Additionstheoreme der Winkelfunktionen.
Das folgende Ausklammern oder Ausmultiplizieren ist verboten: sin(α) + sin(β) ≠ sin(α + β)
Das Bild zeigt die grafische Herleitung für zwei Additionstheoreme. Es geht vom Einheitskreis mit der Strecke OB = 1 aus. Es gilt: (α−β) = (α + (−β)) sowie sin(−β) = −sin(β) und cos(−β) = cos(β). Der Winkel (AOC) ist gleich dem Winkel (OEC), ein sogenannter Z-Winkel. Da bei E ein rechter Winkel ist, muss der Winkel (CEB) den Wert 90°−α betragen. Im rechtwinkligen Dreieck BCE ist der Winkel bei B ebenfalls α.
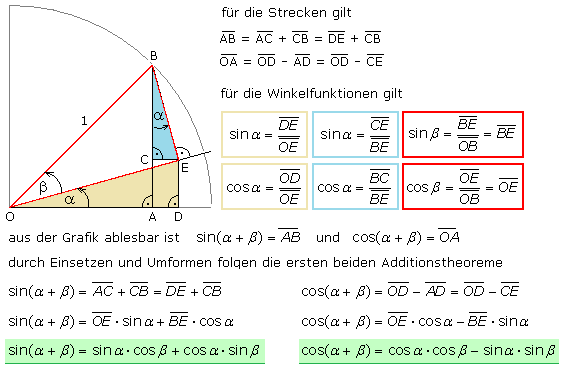
Additionstheoreme der vier wichtigsten Winkelfunktionen
Der Gültigkeitsbereich liegt für Winkel zwischen 0° ≤ α ≤ 90° sowie 0° ≤ β ≤ 90° und 0° ≤ (α+β) ≤ 90°
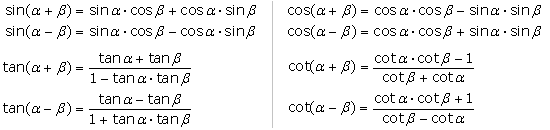 △
△
Trigonometrische Funktionen des doppelten Winkels
Wird die Sinusfunktion des einfachen Winkels f(φ) = sin(φ) als Grundwelle bezeichnet, dann hat die Sinusfunktion des doppelten Winkels g(φ) = sin(2φ) die doppelte Frequenz und ist somit die erste Oberwelle. Die Funktionen lassen sich recht einfach aus den Additionstheoremen herleiten, wobei dann für die Winkel α = β gesetzt wird.
 △
△
Summen und Differenzen einiger Winkelfunktionen
In den Additionstheoremen kommen Summen und Differenzen verschiedener Winkelfunktionen vor. Mit ihrer Hilfe lassen sich die Summen und Differenzen gleicher Winkelfunktionen herleiten. Das wird an einem Beispiel gezeigt, während für einige andere Sinus- und Cosinusfunktionen nur das Ergebnis angegeben wird. Die Tangens- und Cotangensfunktionen sind in der Elektronik nicht so interessant und erscheinen daher hier nicht.

Additionstheorem mit unterschiedlichen Amplituden der Winkelfunktionen
In den mathematischen Formelsammlungen sind die Amplituden der Ausgangswinkelfunktionen stets 1. In der Praxis kommt das seltener vor. Sucht man eine Gesamtformel nach dem Additionstheorem für zwei Winkelfunktionen mit unterschiedlichen Amplituden, so kommt man mit einem mathematischen Trick ans Ziel. Das Ergebnis einer Gleichung ändert sich nicht, wenn man sie um einen Ausdruck additiv erweitert, der sogleich subtrahiert wird. Beide Ausdrücke werden notiert, dann wird die so erweiterte Gleichung umgeformt.
 △
△
Die Produkte einiger Winkelfunktionen
Der Inhalt ist sehr theoretisch und scheint für die Praxis unnötig zu sein. Bei bekannten Winkelwerten kann man sehr leicht mit einem Taschenrechner für jeden konkreten Fall die Summe, Differenz oder das Produkt direkt ermitteln. Die vorgestellten Beziehungen zwischen den Winkelfunktionen sind hilfreich bei der Umformung und Vereinfachung von Gleichungen mit Winkelfunktionen.
 △
△
Funktionsreihen
Die transzendenten Funktionen, hier im Beispiel die Sinusfunktion, lassen sich durch numerische Reihen beschreiben, in denen der x-Wert in immer höheren Potenzen auftritt. Es sind ganz rationale Funktionen, die als Potenzreihen bezeichnet werden. Betrachtet man den Kurvenverlauf der Sinusfunktion, so stellt man fest, dass sich der Bereich des Nulldurchgangs durch eine lineare Ersatzfunktion beschreiben lässt. Ein Teil der folgenden Krümmung entspricht einer Funktionsgleichung der dritten Potenz. Mit einer weiteren Ersatzfunktion noch höherer Potenzen kann die Sinuskurve bis zum Winkel von 90° sehr genau beschreiben werden.
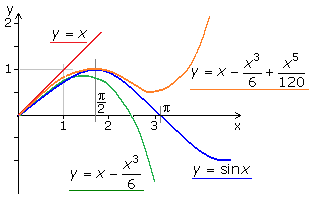
Sind in elektronischen Rechenmaschinen die Funktionswerte der transzendenten Funktionen nicht im ROM-Speicher abgelegt, so werden die Ergebnisse nach entsprechenden Potenzreihen ermittelt. Die Berechnung kann nach wenigen Gliedern abgebrochen werden, wenn der Nenner durch den Fakultätsausdruck sehr groß geworden ist.
