Leitungscodes zur Bit-Übertragung
Die Daten werden im Netzwerk in der physikalischen Ebene übertragen. Es ist die unterste Ebene des an anderer Stelle beschriebenen OSI-Schichtenmodells. Das Übertragungsmedium dieser Ebene ist entweder ein kupferbasiertes oder optisches Leitungssystem. In beiden Fällen erfolgt der Datentransport seriell, um den Installationsaufwand einfach und klein zu halten. Zur elektrischen Übertragung ist eine Doppelleitung notwendig. Das kann ein Koaxial- oder Twisted-Pair-Kabel sein. Beim optischen Medium mit Lichtwellenleitern (LWL) reicht für einen seriellen Datenstrom eine Glasfaser aus. Die digitalen Daten sind vor dem Versenden an das Medium anzupassen, um dessen Eigenschaften optimal auszunutzen. Die Anpassung erfolgt durch einen geeigneten Leitungscode.
- Non-Return-to-Zero / NRZ-Codierung
- Return-to-Zero / RZ-Codierung
- Manchester- und differenzieller Manchestercode
Die Übermittlung des Sendetakts ist eine sehr wichtige Aufgabe der Leitungscodes. Der Datenempfänger muss sich auf den Sender synchronisieren können, um die Daten korrekt auszuwerten. Der Sendetakt könnte dazu auf einer parallelen Leitung, besser aber mit den Daten selber übertragen werden. Der Empfänger kann aus einem seriellen binären Datenstrom mit einer längeren Folge von High- oder Low-Pegelzuständen keine Taktinformation gewinnen.
Ein geeigneter Leitungscode hält den Datenstrom von Gleichspannung frei. Durch ein Ungleichgewicht an High- und Low-Zuständen entstehen auf der Leitung im zeitlichen Mittel DC-Pegel. Bei kürzeren Strecken stört der DC-Anteil die Signalweiterleitung in den Impulsübertragern, die nach oder in den Buchsen der modularen RJ-Stecksysteme verwendet werden. Gleichspannung steuert die Transformatoren in die magnetische Sättigung und verzerrt dadurch die Impulse, womit deren eindeutige Auswertung verhindert wird. Das Bild zeigt die Schaltung einer RJ-45 8P4C Buchse für das 10Base-T und 100Base-T2 Ethernet.
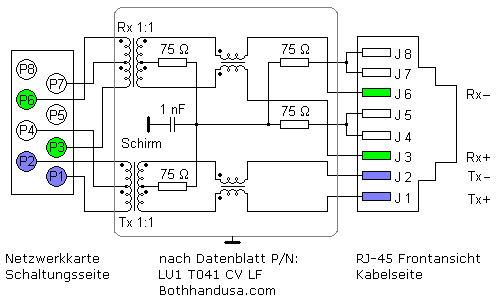
Jedes elektrische Kabel hat Tiefpassverhalten und dämpft zunehmend Signale höherer Frequenz. Mit dem Leitungscode versucht man einen Datenstrom mit geringem Bandbreitenbedarf zu erzeugen. Er wird von der Datenübertragungsrate, das ist die Anzahl der Informationseinheiten, den Bits pro Sekunde, bestimmt. Mit zunehmender Übertragungsrate [bit/s] steigt die Signalfrequenz.
Die Schrittgeschwindigkeit ist ein in diesem Zusammenhang wichtiger Parameter. Sie steht für die Anzahl der Signalwechsel pro Sekunde und wird in Baud (Bd) angegeben. Da die Schrittgeschwindigkeit auch größer als die Datenübertragungsrate sein kann, bestimmt sie den Bandbreitenbedarf.
Die Empfangssignale können nur dann als digitale Signale erkannt werden, wenn der Pegelwechsel mit ausreichend großer Flankensteilheit erfolgt. Die Fouriersynthese zeigt, dass dazu mehrere Harmonische ungedämpft übertragen werden müssen. Die Bandbreite des Übertragungsmediums muss mindestens das Doppelte der Schrittgeschwindigkeit sein.
Beide Verlinkungen geben Erklärungen zu wichtigen Begriffen der Datenübertragung oder in ähnlicher Darstellung mit Kenngrößen digitaler Modulationsverfahren.
Unabhängig vom Leitungscode gibt es zwei weitere Codierungen, die hier nicht näher beschrieben werden. Die Kanalcodierung ermöglicht eine zusätzliche Fehlererkennung und Korrektur. Die Quellencodierung entspricht der Datenkompression.
△NRZ-Codierung
Die Non-Return-to-Zero oder NRZ-Codierung und ist der einfachste digitale Leitungscode. Ein binäres TTL-Signal entspricht einem NRZ-Code. Es gibt zwei unterschiedliche Signalpegel, die beide als Informationsträger dienen, wobei einer der Spannungspegel auch den Wert 0 Volt haben kann. Eine längere Folge gleicher High oder Low Bit-Zustände ergibt auf der Leitung keine Pegeländerungen. Damit der Empfänger den Datenstrom richtig auslesen kann, wird parallel ein Taktsignal mitgesendet. Die Daten können auch als gleichgroße Blöcke gesendet werden. Jedes Datenpaket wird in einem Datenrahmen gepackt und mit Start- und Stoppkennung gesendet. Die NRZ-Codierung ist im zeitlichen Mittel nicht gleichspannungsfrei.
Die serielle RS-232-Schnittstelle arbeitet mit NRZ-Leitungscode und einem Datenrahmen zur Synchronisation. Der logischen Eins ist eine negative Spannung und der logischen Null eine positive Spannung zugeordnet. Der Datenblock hat ein 0-Bit als Startbit, gefolgt von maximal 8 Bit Nutzdaten und einem möglichen Paritätsbit. Der Datenrahmen endet mit einem oder zwei 1-Bit-Zuständen als Stoppsignal. Eine längere Folge von 1-Bit-Zuständen signalisiert, dass keine Daten übertragen werden. Die mit ±12 V hohen Signalpegel erlauben trotz DC-Dämpfung auch lange Kabelsegmente zu verwenden.
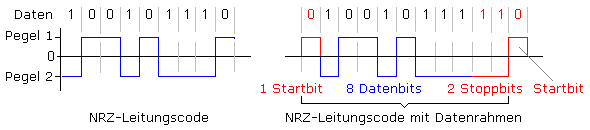
Das linke Teilbild zeigt den Ausschnitt aus einem NRZ-Leitungscode. Das Signal lässt keine Taktrückgewinnung zu. Im rechten Teilbild kann der Empfänger den Takt aus der konstanten zeitlichen Abfolge von Start- und Stoppbits ermitteln.
△RZ-Codierung
Der Return-to-Zero oder RZ-Code führt das Signal nach einem halben Bittakt vom High- oder Low-Pegel in den neutralen Nullzustand zurück. Er gibt drei Sendesymbole, die allgemein mit +1, 0 und −1 bezeichnet werden, wobei ein Datenbit durch zwei Symbole gekennzeichnet ist. Entspricht der High-Pegel als logische Eins einer +1, 0 Folge, dann hat die logische Null als Low-Pegel eine −1, 0 Folge. Die Symbolrate wird durch die RZ-Codierung verdoppelt. Jedes gesendete Bit erzeugt eine Pegeländerung, auf die sich der Empfänger synchronisieren kann. Der RZ-Leitungscode enthält das Taktsignal.
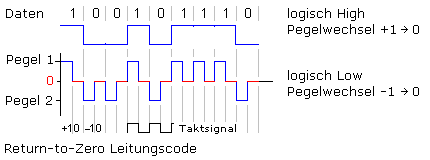
Die Schrittdauer der Binärdaten ist hierbei gleich der Periodendauer des Taktsignals. Die Bitrate oder Bitfolgefrequenz ist nur halb so groß wie Taktfrequenz. Das ist ein Nachteil der Return-to-Zero-Codierung, da das Sendesignal eine größere Bandbreite benötigt oder ohne Signalregeneration nur über eine kürzere Strecke sicher übertragen werden kann. Im zeitlichen Mittel ist der RZ-Code nicht gleichspannungsfrei.
△Manchester-Codierung
Die einfache Bit-Manchester-Codierung teilt ebenfalls jedes Datenbit in zwei Hälften, wodurch der Leitungscode das Taktsignal erhält. Nach dem Ethernet-Standard codiert die ansteigende Flanke im Manchestercode die logische 1 als High-Zustand im Datenstrom. Die fallende Flanke im Manchestercode, bezogen auf die zeitliche Abfolge des Datenstroms steht für die logische 0, dem Low-Zustand des Datenstroms. Die Information ist an die Signalflanken gebunden, die Codierung entspricht damit einem digitalen Phase-Shift-Keying-Verfahren.
In der ursprünglichen Definition des Manchester-Codes, nach G. E. Thomas, bezeichnete der fallende Flankenwechsel ein High-Bit und der ansteigenden Wechsel das Low-Bit. So entsprach der zuerst gesendete Wert im Leitungscode direkt dem Datenwert. Vergleicht man den Leitungscode beider Verfahren, so sind sie zueinander invertiert. Ist das Verfahren nicht grundsätzlich bekannt, dann wird vor dem Datenstrom ein definiertes Bitmuster, die Präambel gesendet.
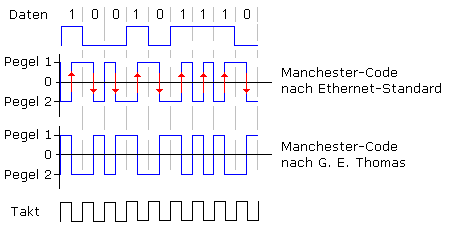
Die Manchester-Codierung erzeugt einen gleichspannungsfreien Leitungscode. Die Signalpegel wechseln zwischen ±0,85 V. Von Nachteil ist der doppelte Bandbreitenbedarf aufgrund des Pegelwechsels innerhalb jedes Datenbits. Der Leitungscode weist maximal nur zwei gleiche Zustände in Folge auf, die dann aber zur Hälfte zwei unterschiedlichen Datenbits zugeordnet sind. Die Tabelle zeigt dazu einige Beispiele binäre Bytes und deren Manchester-Code:
| Dezimalzahl | Binärcode, 1Byte | Manchester-Code |
|---|---|---|
| 0 | 00000000 | 1010101010101010 |
| 255 | 11111111 | 0101010101010101 |
| 153 | 10011001 | 0110100101101001 |
| 113 | 01110001 | 1001010110101001 |
Im Videoclip wird an zwei Beispielen die Umwandlung einer alphanumerische Eingabe zum jeweiligen Manchestercode gezeigt. Der Eingabestring wird zuvor in seinen ASCII-Code, eine Dezimalzahl und diese in ihren Binärcode gewandelt und angezeigt. Das Video zeigt die Codierung für zwei Eingabestrings. Der Ablauf kann nur mithilfe der Controlleiste gesteuert werden.
Differenzielle Manchester-Codierung
Der differenzielle Manchester-Code ist eine Weiterentwicklung der Manchester-Codierung und wird beim Token-Ring-Verfahren eingesetzt. Bei der Codierung moduliert der Binärcode die Phasenlage des Taktsignals. Der resultierende Leitungscode enthält das Taktsignal und ist selbstsynchronisierend. Im Allgemeinen werden die folgenden Codierregeln angewendet:
- Ein Polaritätswechsel zum Taktbeginn kennzeichnet eine logische Null (Low).
Der Low-Zustand weist zwei Flankenwechsel auf.
Beim Wechsel von Low nach High bleibt die Polarität des Leitungscodes unverändert. - Kein Polaritätswechsel zum Taktbeginn kennzeichnet eine logische Eins (High).
Der High-Zustand weist einen Flankenwechsel auf.
Beim Wechsel von High nach Low ändert sich die Polarität des Leitungscodes.
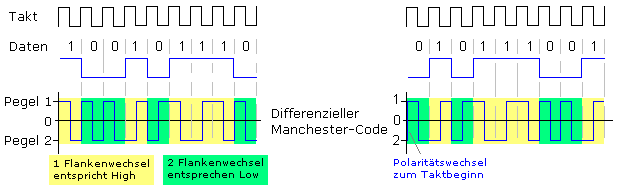
Es besteht auch hier eine zweite gleichwertige Regel, bei der nur die binären Eingangszustände ausgetauscht sind. Beim differenziellen Manchester-Code ist die Datenrückgewinnung unabhängig von der Polarität des Leitungssignals. Der Leitungscode bleibt im zeitlichen Mittel frei von Gleichspannungsanteilen.