Pulscodemodulation – PCM
Modulationsverfahren sind die Voraussetzung einer gemeinsamen Signalübertragung im selben Medium. Unsere Sinnesorgane können analoge Informationssignale nicht in ihrer vollen Kontinuität erfassen. Wir können nur eine endliche Zahl von Intensitätsunterschieden wahrnehmen. Wird ein analoges Informationssignal auf die Anzahl der wahrnehmbaren Stufen reduziert, so kann die Information weiterhin einwandfrei erkannt werden. Dieser Ansatz führte 1938 zu einer Patentanmeldung über die Abtastung und Quantisierung von Sprachsignalen, um sie codiert zu übertragen. Das neue Verfahren erhielt die Bezeichnung Pulscodemodulation (PCM). Nach der Beschreibung der PCM-Methode werden die wichtigsten Kenngrößen digitaler Modulationsverfahren aufgezählt und die Daten zur ISDN-Fernsprechtechnik mit PCM30 vorgestellt.
Abtastung mittels Sample and Hold
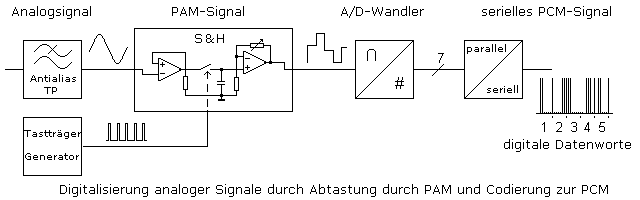
Beim PCM-Verfahren wird ein Analogsignal zuerst durch Abtastung in ein zeitdiskretes PAM-Signal gewandelt. Das noch immer in der Amplitude kontinuierliche Signal lädt vom Abtasttakt gesteuert einen Kondensator auf. Beide Vorgänge arbeiten mit demselben Tastträger und werden innerhalb eines Funktionsblocks, der Sample and Hold Stufe ausgeführt. Das Ausgangssignal ist ein zeitdiskretes und in den Amplitudenabschnitten linearisiertes PAM-Signal mit stufenförmigem Verlauf. Die Amplituden der Stufen sind nicht wertediskret, denn sie verändert sich proportional mit der Amplitude des Eingangssignals.
Quantisierung
Die Maximalamplitude des Sample&Hold-Signals wird auf die Wandlerkennlinie eines Analog- zu Digitalwandlers, A/D-Wandler angepasst. Sein Arbeitsbereich soll angenommen zwischen ±5 V liegen. Wird dieser Bereich linear mit einem 7-Bit A/D-Wandler in binäre Datenworte gewandelt, so stehen sowohl für positive als auch negative Signalspannungen 26 = 64 Amplitudenwerte zur Verfügung. Ein Bit ist für den Vorzeichenwechsel beim Nulldurchgang notwendig. Das Einteilen des Amplitudenbereichs in definierte Spannungsstufen wird Quantisierung genannt.
Codierung
Das durch Sample&Hold generierte und mittels Quantisierung angepasste PAM-Signal wird letztlich in ein digitales Signal umgesetzt. Der A/D-Wandler liest dazu in den Tastpausen der Sample&Hold-Stufe den aufbereiteten Spannungswert aus und codiert ihn in ein paralleles Datenwort. Der wohl einfachste A/D-Wandler erzeugt einen Binärcode mit einer Signalfolge aus High- und Low-Signalen. Die Ausgangssignale des Wandlers werden vor dem nächsten Takt seriell ausgelesen.
Aus dem Analogsignal ist über ein PAM-Signal das entsprechende PCM-Signal geworden. Das PCM-Signal ist sowohl zeit- als auch wertediskret. Es gibt mit High und Low nur zwei unterschiedliche Amplitudenwerte mit einer konstanten Taktfolge. Bis auf die notwendige PAM-Signalanpassung an den A/D-Wandlerbereich lässt sich die Quantisierung und Digitalisierung als ein einziger Vorgang sehen. Die Art der Quantisierung wird von der Methode der A/D-Wandlung bestimmt. Das Diagramm veranschaulicht mit Blockschaltbildern die Pulscodemodulation.
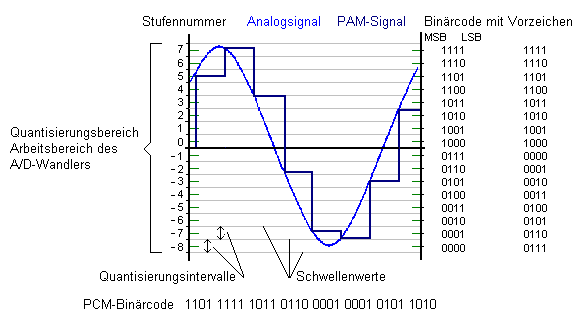
Das nächste Bild zeigt die Quantisierung und Codierung einer bipolaren PAM durch einen 4-Bit A/D-Wandler. Der Arbeitsbereich des Wandlers umfasst 24 = 16 Stufen. Jedem Quantisierungsintervall ist ein Binärcode zugeordnet. Das höchst wertige Bit oder most significant bit (MSB) hat bei allen Intervallen, die im Positiven liegen, den Wert 1 und für Intervalle im negativen Bereich den Wert 0. Der Spannungswert 0 V bleibt in diesen Beispielen uncodiert.
Die linke Binärcodereihe wird Zweierkomplement genannt. Daneben ist eine weitere Möglichkeit für Dualzahlen mit Vorzeichenkennung zu sehen. Überschreitet der PAM-Abtastwert die untere Schwelle eines Intervalls, so erhält er den entsprechenden Binärcode des Intervalls. Reicht das Tastsignal über die obere Schwelle dieses Intervalls, so wird ihm der nächsthöhere Codewert zugeordnet.
Wenn n die Anzahl der Binärstellen im Codewort ist, errechnet sich der Wertebereich bei Dualzahlen mit Vorzeichen zu:
−2n−1 ... 2n-1 − 1 und für Dualzahlen ohne Vorzeichen zu:
0 ... 2n − 1. Aus der Anzahl der Binärstellen ergibt sich mit 2n die Zahl der Quantisierungsstufen oder Intervalle.
Quantisierungsfehler
Nicht erfasst werden können Amplitudenänderungen des Analogsignals, die innerhalb eines Quantisierungsintervalls liegen. Ein aus dem PCM-Signal zurückgewandeltes Analogsignal entspricht daher nie vollkommen dem ursprünglichen Eingangssignal. Für jedes Intervall kann ein Quantisierungsfehler aus der Differenz beider Signale ermittelt werden. Im Arbeitsbereich des A/D-Wandlers liegt der Quantisierungsfehler zwischen ±ΔU/2, wobei ΔU für das Quantisierungsintervall steht. Die Differenz aus dem zurückgewandelten PCM-Signal und dem Originalsignal bildet ein neues, eigenständiges Signal, das Quantisierungsgeräusch.
Der Quantisierungsfehler ist von der Anzahl der Bitstellen abhängig. Bezogen auf den gleichen Arbeitsbereich würde ein 5-Bit A/D-Wandler die Intervalle und damit den Fehler halbieren. Für Sprach- und Musiksignale ist die lineare Quantisierung nicht ideal. Bei einem konstant angenommenen Störpegel ist für kleine Signalpegel der Signal/Rauschabstand besonders groß. Dem entgegen wirkt ein Kompressionsverfahren, bei dem die kleineren Amplituden mehr und größere Amplituden weniger verstärkt werden.
Die A/D-Wandlung mit Kompandierung arbeitet meistens mit einer logarithmischen Kennlinie und stellt für kleine Signalamplituden mehr Quantisierungsintervalle zur Verfügung als für große Eingangsamplituden. Der Quantisierungsfehler im unteren Bereich ist daher kleiner. Auf der Empfängerseite wird durch den entgegengesetzten Prozess mit einem Expander bei der D/A-Wandlung mit inverser Kennlinie der ursprüngliche Dynamikbereich des Signals wieder hergestellt.
Vor- und Nachteile der PCM
Durch ein Zeitmultiplexverfahren kann dieselbe Übertragungsstrecke mehrfach genutzt werden. Die Qualität der Übertragung bleibt störunempfindlich, wenn auf langen Strecken abschnittsweise sogenannte Regenerativverstärker eingesetzt werden. Die Grafik zeigt, dass sich auch bei verschliffenen Signalen die rechteckförmigen Bitmuster regenerieren lassen, sofern das Taktsignal wiedergewonnen werden kann. Der im Eingangssignal vorkommende Amplitudenschwund und neue Rauschanteile werden dabei nicht erfasst. Einzig das Quantisierungsgeräusch bleibt erhalten. Die digitalen Daten des PCM-Verfahrens sich einfach und sicher zu speichern.
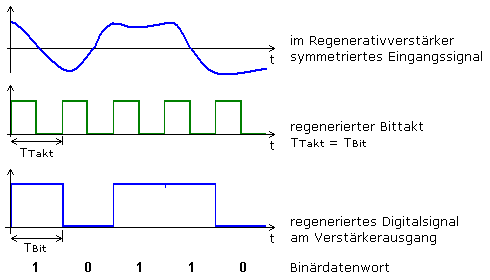
Von Nachteil ist der hohe elektronische Aufwand im Sender und Empfänger für die unterschiedlichen Verfahren wie PAM, Multiplex, AD- und DA-Wandlung sowie steilflankige Tiefpassfilter. Der Bandbreitenbedarf der Übertragung ist sehr hoch. Das Quantisierungsgeräusch tritt als neues, bleibendes Störsignal auf.
Lehrfilm zur PAM / PCM
Die Pulscodemodulation mit Quantisierung und Quantisierungsfehler wird im Zusammenhang mit der vorangehenden Pulsamplitudenmodulation PAM im folgenden Videoclip dargestellt. Weitere darin anschaulich behandelte Themen sind das Shannon-Theorem, die Unterabtastung mit dem Aliasing und das Oversampling im Zusammenhang mit der Dämpfungscharakteristik der notwendigen Tiefpassfilter. Gezeigt wird auch das Prinzip des Zeitmultiplexverfahrens für 3 Kanäle. Die Rückgewinnung der analogen Information durch Decodierung und anschließender Demodulation am Tiefpass vervollständigen den Film.
Die Buttons im Videoclip lassen sich nicht bedienen. Zum Lesen der zum Teil längeren Texte bitte das Video mit der einblendbaren Control-Leiste steuern.
△Kenngrößen digitaler Modulationsverfahren
Die Informationseinheit
Mit einem Bit, dem binary Digit, der kleinsten Informationseinheit in digitalen Systemen, lassen sich genau zwei Zustände darstellen. Das Bit kann mit High = 1 gesetzt oder mit Low = 0 nicht gesetzt sein. Mit 2 Bit lassen sich 4 Zustände erfassen und mit 3 Bit sind es 8. Allgemein errechnet sich die Zahl der Zustände z aus der Anzahl der Bits n zu: z = 2n.
Abtastrate – Sampling rate
Sie wird auch als Abtastfrequenz bezeichnet und stellt die Zeit zwischen zwei Abtastungen einer Sample&Hold-Schaltung (Samples / s) dar. Erfolgt die Abtastung einmal pro Millisekunde, also mit 1 kHz dann gilt für die Abtastrate 1000 S / s. Die Abtastfrequenz muss mindestens etwas mehr als das Doppelte der höchsten abzutastenden Signalfrequenz sein.
Die Bitrate
Die Bitdauer innerhalb eines PCM-Signals ist gleich. Sie bestimmt die maximale Zeichenübertragung pro Sekunde und wird als Bitrate, Bitfolgefrequenz bzw. Schrittgeschwindigkeit bezeichnet.
Die Einheit Bit/Sekunde wird Baud genannt und mit Bd abgekürzt.
fBit = vBit = 1 / TBit in Bd
Die Informationsmenge
Die Quantisierung eines Informationssignals bestimmt mit den Quantisierungsstufen die Anzahl der Zustände z und damit die Zahl der Informationseinheiten:
n = log2(z). Beide Bit-Zustände 0 und 1 zählen als Informationseinheit. Eine in der Bandbreite begrenzte Zeitfunktion erzeugt unter Einhaltung des Abtasttheorems nach Shannon genau 2 · B · T Werte.
Sie sind durch die Quantisierung mit n Informationseinheiten codiert. Die Informationsmenge I errechnet sich aus dem Produkt:
I = 2 · B · T · log2(z) in Bit mit der Übertragungszeit T in s
Die Nyquistbandbreite
Um das Signal im Empfänger eindeutig zu rekonstruieren, muss mindestens die erste Harmonische der höchsten im Signal auftretenden Frequenz übertragen werden. Diese Frequenz wird als Nyquistfrequenz oder Punktfrequenz bezeichnet. Sie ist gleichzeitig die Grundfrequenz eines periodischen High-Low-High-Wechsels, bei der Pulszeit und Pulspause identisch sind. Die Pulsfolgezeit beträgt somit
TP = 2 · TBit. Die Nyquistbandbreite BN ist durch die folgende Beziehung gegeben:
BN = fP = 1 / (2 · TBit) = fBit / 2 in Hz
Die Zeichengeschwindigkeit
Ein komplettes Datenwort beginnt meist mit einem Startbit und endet mit einem oder zwei Stopbits. Dazwischen liegen die eigentlichen Datenbits, manchmal folgt noch ein Paritätsbit. Diese Einheit wird Zeichenrahmen genannt und hat die Übertragungsdauer TZ. Die Dauer der einzelnen Bits im Rahmen soll gleich sein, ihre Gesamtzahl sei Z. Die Zeichengeschwindigkeit ist dann definiert als:
vZ = 1 / TZ in
s−1 mit TZ = Z · TBit
Die Baudrate
Die Baudrate wird auch Übertragungsgeschwindigkeit vü genannt. Im Binärcodesystem ist sie identisch mit der Bitrate oder Schrittgeschwindigkeit. Sie ist neben der Bandbreite auch von der Zahl der Kennzustände n des Datensignals abhängig. Das Binärsignal besitzt 2 Kennzustände. Ternäre oder quaternäre Tastverfahren unterscheiden im Datensignal zwischen 3 bzw. 4 Zuständen:
vü = vBit · lb(n) in Bd oder
vü = Z · vz · lb(n)
mit lb(n) = log2(n) = log(n) / log(2)