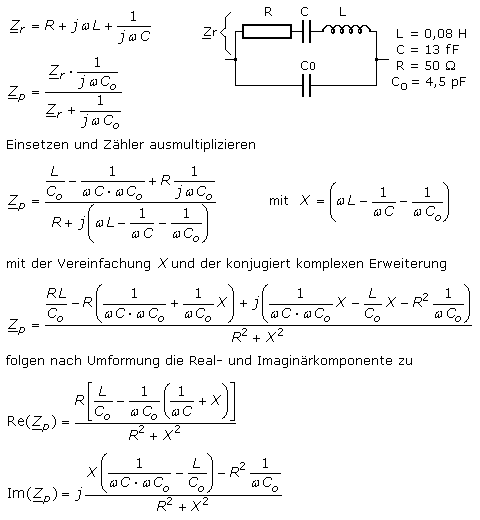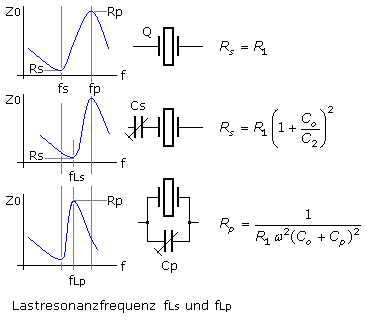Quarzresonator – Quarzoszillator

Kristallines Siliziumdioxid ist ein sehr häufiges Mineral, aber reine und große Quarzkristalle, und nur die eignen sich zur Herstellung von Schwingquarzen als wichtige elektronische Bauteile, sind seltener zu finden. Recht interessant kann es daher auch sein, etwas über viele Jahrzehnte mit dem Schwingquarz einhergehende technische Entwicklung zu erfahren. Leser meines Webprojekts, die nicht nur eine Einführung in die elektronischen Eigenschaften haben wollen, können hier eine freie PDF-Veröffentlichung einer umfangreichen Literaturrecherche per Download erhalten. Vom Herausgeber habe ich die Erlaubnis erhalten, die entsprechenden Links zu schalten, und komme seinem Wunsch gerne nach. Es handelt sich um die E-Book-Fassung Schwingquarze Geschichte und Technik von Heinz Claus, Herausgeber: Adalbert Helwig, 2018. Das E-Book kann als PDF-Datei (565 Seiten, ca. 76 MB) direkt von meiner Domain geladen werden. Nutzer von iTunes–Apple-Systemen mit passendem Account können den zweiten externen Download-Link verwenden.

Quarzresonator

• Resonanzverhalten des Quarzresonators
• Herleitung der Quarz-Ersatzschaltung
• Prinzipschaltungen mit Quarzresonatoren

Bestimmte sehr reine Quarzkristalle eignen sich als elektronische Schwingquarze. Der Quarzkristall sollte mit fehlerfreiem Kristallgitter in der α-Siliziumdioxidmodifikation kristallisiert ist. Unter hohem Druck bilden sich in natürlichen Gesteinshohlräumen aus hydrothermalen Lösungen teils sehr große Einzelkristalle, vielfach aber Kristallgruppen. Sie werden als farbloser Bergkristall oder mit Fremdatomen verunreinigt als gelber Citrin und oft als violetter Amethyst gefunden.

Quarzsynthese

Der natürliche Quarzkristall weist oftmals Störungen im Kristallgitter und mehrfache Zwillingsbildungen auf. Anfangs war es schwierig, aus natürlichem Bergkristall gute Schwingquarze zu schneiden. In der Elektronik wird ab 1960 ausschließlich Synthesequarz verwendet. Die synthetische Herstellung erfolgt aus hydrothermaler Lösung im senkrecht stehenden Autoklav bei sehr hohem Druck und hoher Temperatur. Quarzbruch reagiert unter diesen Bedingungen mit Natriumhydroxid- oder Natriumkarbonatlösungen und bildet übersättigte Lösungen. Die Konvektionsströmung im Autoklav scheidet am kühleren oberen Ende bei rund 390°C an dort eingebrachten Kristallkeimplatten Quarzkristalle ab. Die Synthesezeit dauert 1 bis 3 Monate. Je länger der Prozess dauern darf, desto reiner und wertvoller sind die Einkristalle.

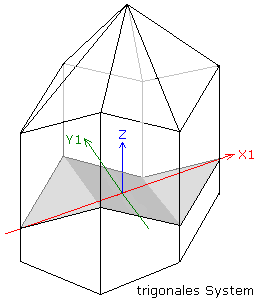
Der α-Quarz oder Tiefquarz kristallisiert im trigonalen Kristallsystem. Das Gitter baut sich aus SiO4-Tetraeder auf, in denen ein positiv vierwertiges Siliziumion von vier zweiwertig negativen Sauerstoffionen in kovalenter Bindung umgeben ist. Die Tetraeder sind dreidimensional über ihre Ecken verknüpft. Im Kristallgitter zeigen sich sechsringförmige Leerräume. Beim Tiefquarz liegen sie nicht in einer Ebene, sondern in einer energetisch günstigeren Sesselform. Das verhindert eine für alle Kristallachsen vollkommene Symmetrie, wodurch polare Achsen entstehen. Sie sind eine Voraussetzung für die piezoelektrischen Eigenschaften. Als Schwingquarz kann nur die α-SiO2 Modifikation verwendet werden. Oberhalb von 573° bildet sich der β-Quarz als Hochquarz im hexagonalen Kristallsystem. Die Sechsring-Sesselform wechselt unter Beibehalten der Bindungsart in die ebene Sechsringform des Hochquarzes. Mit der Symmetrieänderung gehen die piezoelektrischen Eigenschaften verloren. Beim Abkühlen entsteht wieder die α-Modifikation des Tiefquarzes, wobei sich im Gitter vielfach Zwilligskristallstrukturen bilden, deren piezoelektrische Eigenschaften einander entgegengesetzt sind. Der Kristallquerschnitt ist sechseckig und die Kristallsäulen können in symmetrisch mehrflächigen Spitzen enden.

Piezoelektrizität

Werden die kristallografischen Achsen mit x, y und z bezeichnet, dann ist die z-Achse die Längsachse der Säule. Sie geht durch die Spitzen und gilt als optische Achse. Senkrecht dazu verlaufen in der Ebene des hexagonalen Prismas die x- und y-Achsen. Die x-Achse, auch elektrische Achse genannt, steht mit dem direkten Piezoeffekt in Verbindung. Im sechseckigen Querschnitt gehen die drei x-Achsen durch die gegenüberliegenden Ecken, den Säulenkanten des Kristalls. Die elektrische Anregung in Richtung einer x-Achse erzeugt eine Längenänderung in der zugehörigen y-Achse. Senkrecht zu jeder der x-Achsen gibt es je eine y-Achse durch die Kristallflächen. Die y-Achsen werden als mechanische Achsen bezeichnet und sind für den indirekten Piezoeffekt verantwortlich. Mechanischer Druck oder Zug in y-Achsenrichtung erzeugt einen Ladungsaufbau in der zugehörigen x-Achsenrichtung.

Schwingquarze geben in Oszillatorschaltungen die Referenzfrequenz und werden in speziellen Filterschaltungen mit sehr großer Flankensteilheit eingesetzt. Quarze übertreffen durch die Nutzung ihrer mechanischen kristallurgischen Eigenschaften die elektrischen Eigenschaften der herkömmlichen RLC-Schaltungen. Die Kristalle sind sehr gute Isolatoren. Die elektrisch nutzbaren Eigenschaften sind wenig temperaturabhängig und über lange Zeit resistent gegen Umwelteinflüsse. Als Einkristalle übertreffen sie darin die ebenso nutzbaren polykristallinen Piezokeramiken. Die piezoelektrischen Eigenschaften der Quarze sind allerdings geringer als die der Piezokeramiken.

Aus dem Quarzeinkristall wird eine Scheibe, ein Band oder kleiner Balken geschnitten und anschließend per Feinschliff auf die gewünschte Frequenz hin bearbeitet. Mit den vielfältigen Kristallschnitten lassen sich die fertigen Schwingquarze zu Dehnungsschwingungen, Biegeschwingungen, Flächenscherungs- oder Dickenscherungsschwingungen anregen. Das erschließt ein weites Frequenzspektrum, wobei jeder Quarzoszillator nur auf seiner Eigenresonanz oder einer Oberwelle schwingen kann. Sie ist von der Kristallstruktur und dem Kristallschnitt bestimmt.

Die piezoelektrischen und mechanischen Parameter sind von der Richtung und den Achsen abhängig. Wirken keine weiteren Störungen auf den Kristall ein, dann ist der longitudinale direkte Piezoeffekt direkt proportional zur einwirkenden Kraft. Eine mechanische Kraft in x-Achsenrichtung erzeugt Ladungen auf den x-Flächen. Dort angebrachte Elektroden wirken als Kapazität und nehmen die Ladungsverschiebung auf. Sie kann unter Berücksichtigung der kapazitiven Belastung durch die Messanordnung als Spannung bestimmt werden.

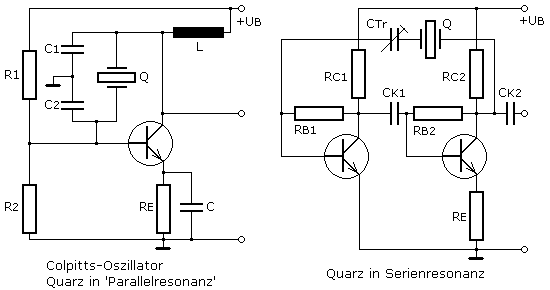
Quarze als Oszillatorbauteil

Dehnungsschwinger sind plattenförmig und schwingen longitudinal in Richtung der längeren y-Achsenrichtung. Biegeschwinger sind x-Schnitt Dehnungsschwinger mit zwei gegenphasig angeschlossenen Elektroden. Die Biegung erfolgt in z-Achsenrichtung. Stimmgabelquarze sind in Form einer Stimmgabel im x-Schnittverfahren als Biegeschwinger hergestellt. Flächendehnungsschwinger sind meistens quadratische oder rechteckige Kristallplatten mit definierten Kantenlängen. Je nach Schnittart liegt der Frequenzbereich der Eigenresonanz zwischen 180 kHz bis 800 kHz. Auf dem Resonatorkristall sind an den Stellen der Schwingungsknoten die Elektroden befestigt, an denen die Drähte angelötet sind. Dickenscherungsschwinger werden im Eigenresonanzbereich von 1 MHz bis 250 MHz eingesetzt. Die Elektroden befinden sich in der Scheibenmitte, da es keine Schwingungsknoten an den Außenflächen gibt.

Schwingquarze sind passive Bauteile, die sich erst bei geeigneter elektrischer Anregung wie ein Schwingkreis sehr hoher Güte verhalten. Die mechanische Schwingungsamplitude des Kristalls ist proportional zur Wechselstromamplitude. Im Resonanzfall kann dem Quarz ein niedriger ohmscher Resonanzwiderstand zugewiesen werden. Außerhalb der Resonanz ist der Quarz hochohmig. Ein zu großer Resonanzstrom kann den Resonator zerstören, da das Kristallgitter den zunehmenden mechanischen Belastungen nicht gewachsen ist.

Quarze sind einer Langzeitalterung unterworfen, bei der sich ihre Frequenz ändert. Im Kristallgitter können sich bei Überlastung Störstellen ausbilden. Im Gitter vorhandene Fremdatome oder aus den Metallelektroden beziehungsweise der Umwelt eindiffundierende Fremdatome verändern ihre Gitterposition und damit die Kristalleigenschaften. Hochwertige Quarze sind in evakuierten Gehäusen gegenüber Umwelteinflüssen geschützt. Die Frequenzdrift eines Quarzoszillators ist wesentlich geringer als die herkömmlicher RLC-Oszillatoren. Sie liegt aufgrund der Langzeitstabilität bei Serienquarzen um Δf/f ≈ 10⁻⁶ und bei Präzisionsquarzen um Δf/f ≈ 10⁻⁹. Quarze erreichen ihren stabilen Langzeitwert erst nach einer gewissen Einlaufzeit. Auch im temperaturstabilisierten Quarzofen wird die Frequenzstabilität erst nach einiger Zeit erreicht. Das Aufheizen sollte langsam erfolgen, um die damit verbundenen mechanischen Belastungen auf den Resonator gering zu halten.

Der Schwingquarz und sein Ersatzschaltbild

Das allgemeine Ersatzschaltbild zeigt eine Reihenschaltung aus R, L und C und dazu parallel eine weitere Kapazität. Die Bauteile der Reihenschaltung stehen für die dynamischen Größen des Kristalls. Der Widerstand R1 entspricht dem Resonanzwiderstand im elektrischen Schwingkreis. Er steht in Verbindung mit den mechanisch-dynamischen Schwingungsverlusten im Kristallgitter, der Kristallhalterung und der Gasatmosphäre im Quarzgehäuse. Die Serienkapazität C1 oder dynamische Kapazität wird von der elastischen Nachgiebigkeit des Kristallgitters und der piezoelektrischen Konstanten bestimmt. Die Werte werden in Femtofarad angegeben. Die Reiheninduktivität L1 steht mit der mechanisch schwingenden Masse des Resonators in Verbindung, wobei die elektrischen Werte im Henrybereich liegen. Die Parallelkapazität C0 ist eine statische Größe und direkt messbar. Sie setzt sich aus der Elektrodenkapazität CE beidseitig der Resonatorplatte, den Streukapazitäten zur Innenseite des Metallgehäuses und dem Kapazitätswert der Anschlussbeinchen zusammen. Die gesamte Parallelkapazität beträgt einige Picofarad.

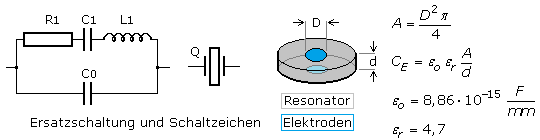
Die Elektrodenkapazität ist zusätzlich von der im Schwingkreis genutzten Oberwelle abhängig. Es besteht die Beziehung: C_E ≈ 2·10⁻⁵ · D² · f / n mit dem Elektrodendurchmesser D in mm, der Eigenresonanz f und der Oberwellenzahl n. Im Schaltungskonzept sollte anstelle der Parallelresonanz C0 besser von der Lastkapazität CLast gesprochen werden. Sie ist die Summe aller zum Quarz parallel und in Serie liegenden Schaltungskapazitäten. Parallel zum Quarz geschaltete Kapazitäten können den Lastresonanzwiderstand so weit vergrößern, dass die Schwingung abbricht. Ziehkondensatoren zur Feineinstellung der Frequenz sollten daher in Reihe geschaltet werden.

Resonanzverhalten des Quarzresonators

Die Ersatzschaltung lässt vermuten, dass es zwei Frequenzen geben wird, bei der die Impedanz der Schaltung reell wird. Experimente zeigen, dass Schwingquarze bei Eigenresonanz eine sehr hohe Güte aufweisen. Das gilt für den im Ersatzschaltbild erkennbaren Reihenschwingkreis nur bei einem sehr kleinen Serienwiderstandswert. Wird er im Idealfall als vernachlässigbar klein angesehen, vereinfacht sich das Aufstellen der komplexen Impedanzgleichung. Die komplexe Reihenimpedanz aus C1 und L1 liegt parallel zur komplexen eingesetzten Lastkapazität C0 und erlaubt folgende Berechnung:

Aus der idealisierten Gleichung Gl.(1) lassen sich zwei Frequenzen ermitteln. Im Fall der Serienresonanz hat die imaginäre Komponente den Wert null. Bei einem idealen Parallelschwingkreis strebt die Impedanz gegen unendlich. Das ist für die Gl.(1) dann der Fall, wenn der Nenner den Wert null annimmt.

Für die Gleichung der Parallelresonanz findet man oft auch eine andere Schreibweise. Sie ist gleichwertig und folgt aus der Gl. (3) nach einigen Formelumstellungen. Für den rechten Wurzelausdruck wird der Hauptnenner erstellt und die rechte Seite unter eine gemeinsame Wurzel gestellt.

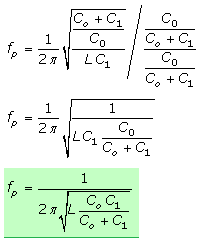
Aus Gl. (2) und Gl. (3) erhält man durch Umformen ein Verhältnis zwischen der dynamischen Kapazität C1 und der statischen Parallelkapazität C0. Der Kehrwert wird als r bezeichnet. Man erkennt damit auch, dass der Abstand beider Frequenzen zueinander sehr gering ist.

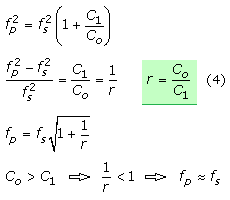
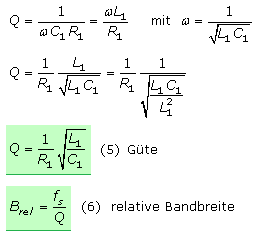
Resonatorgüte und Bandbreite

Verglichen mit RLC-Oszillatoren zeichnen sich Quarzresonatoren in Schwingkreisen durch eine sehr viel höhere Güte aus. Das ergibt sich auch aus der im Verhältnis zur dynamischen Kapazität extrem großen Induktivität des Quarzes. Mit diesen Eigenschaften haben Quarzoszillatoren eine sehr geringe Bandbreite. Die mathematische Herleitung erfolgt für die Serienresonanz unter Vernachlässigung der Parallelkapazität.

AC-Analyse im Bereich der Resonanzfrequenz

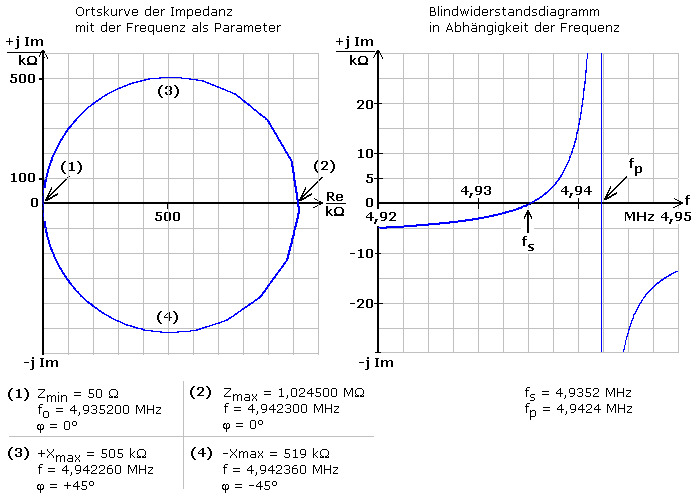
Mit einem Simulationsprogramm wurde ein in der Datenbank zur Verfügung stehender 5 MHz Quarz mit bekannten Daten der AC-Frequenzanalyse (Bodediagramm) unterzogen. Das Bild zeigt den Amplituden- und Phasenfrequenzgang und die daraus ermittelbaren Resonanzfrequenzen, die mit den mathematisch errechenbaren Frequenzen übereinstimmen.

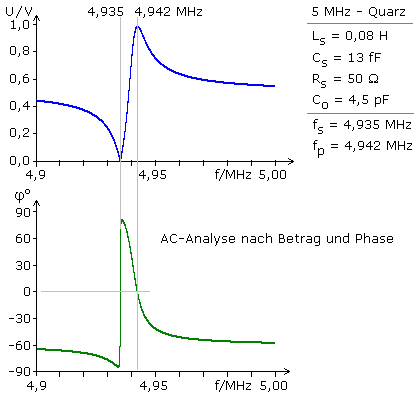
Im Bereich der Serienresonanzfrequenz ist der Quarz sehr niederohmig, der Phasenwinkel wird zu null und nach außen wirkt der Resonator mit seinem Serienwiderstand. Die Kurve zeigt bei etwas höherer Frequenz erneut reelles Verhalten mit dem Phasenwinkel φ = 0°. Dazwischen weist der positive Phasenverlauf auf ein induktives Verhalten des Resonators hin. Die Serienresonanzstelle und ein Bereich in Richtung der höheren sogenannten Parallelresonanz werden in Oszillator- und Filterschaltungen verwendet.

Herleitung der Quarz-Ersatzschaltung

Das Resonanzverhalten eines Quarzresonators wurde weiter oben idealisiert ohne den ohmschen Widerstand hergeleitet. Er soll jetzt berücksichtigt werden. Das Ziel ist es die Gleichungen für die Real- und Imaginärkomponente der komplexen Impedanz zu erhalten.

Die beiden Gleichungen eignen sich gut zur programmierten Darstellung der Ortskurve und des Verlaufs der Blindwiderstandskurve eines Quarzresonators. Die Kurven entstanden mit den angegebenen Quarzwerten aus einer SPICE-Datenliste. Für beide Kurven durchlief die Programmschleife den Frequenzbereich 4,92 ... 4,95 MHz in 10 Hz-Schritten und schloss damit die Resonanzfrequenzen der SPICE-Liste ein. Die Werte der gekennzeichneten Kurvenpunkte wurden aus den gespeicherten Rechenwerten des Programms ermittelt.

Serienresonanz

An den Stellen (1) und (2) schneidet die Ortskurve die Re-Achse. An (1) mit dem Phasenwinkel φ=0° ist die Impedanz ausschließlich reell mit dem Wert Z = 50 Ω. Es ist die Serienresonanzstelle für den hier untersuchten Quarz mit f0 = 4,9352 MHz. Aus den gespeicherten Programmwerten konnte symmetrisch mit φ = ±45° um diesen Resonanzpunkt der Frequenzabstand mit Δf = 100 Hz ermittelt werden. Dieser Wert entspricht dem aus der Bandbreitenformel Gl.(5) mit Q ≈ 49600 und Gl.(6) mit B ≈ 100 Hz bei Serienresonanz überein.

Antiresonanz

An der Stelle (2) ist die Impedanz wiederum reell und der Phasenwinkel φ = 0°. Die gespeicherten Programmwerte zeigen hier den Maximalwert der Impedanz mit Z = 1,025 MΩ. Die zugehörige Frequenz f = 4,9423 MHz entspricht den SPICE-Daten der Parallelresonanz. In vielen Veröffentlichungen zum Verhalten der Quarzresonatoren handelt es sich um die Antiresonanzfrequenz fa. Sie liegt noch unterhalb der Parallelresonanz fp, wo der Phasenwinkel negativ ist und die Impedanz Z ihren Maximalwert hat.

Für diesen Resonator zeigen die mathematischen Ergebnisse mit der zur reellen Achse fast spiegelsymmetrischen Ortskurve keinen prägnanten Unterschied zwischen der Antiresonanz und der Parallelresonanz. Bei den Punkten (3) und (4) auf der Ortskurve bilden die Impedanzzeiger mit der reellen Achse einen Winkel von ±45°. Auch hier beträgt der Frequenzabstand Δf = 100 Hz und entspricht der Bandbreite bei der Serienresonanz.

Das Blindwiderstandsdiagramm zeigt, dass der Quarzresonator in Oszillatorschaltungen bei seiner Antiresonanz praktisch nicht nutzbar ist. Das Verhalten bei f(a)p ist zu beiden Seiten extrem hochohmig und springt an der Asymptote von maximal induktiv zu maximal kapazitiv. An der Serienresonanzstelle ist ein schmalbandiger, kontinuierlich nutzbarer Übergang vorhanden.

Lastresonanz

Quarzresonatoren können in Oszillatoren mit LC-Parallelschwingkreisen die Induktivität der Spule ersetzen. Der Quarz arbeitet dann im Bereich oberhalb seiner Serienresonanz und zeigt dort hochohmiges induktives Verhalten. Die zugehörige Resonanzfrequenz wird als Lastresonanz fL bezeichnet. Sie liegt zwischen der Serienresonanz- und der Antiresonanzfrequenz. Die Kapazitäten des Parallelschwingkreises und zugeschalteter Ziehkondensatoren bilden mit der statischen Kapazität des Quarzresonators die Lastkapazität für den Quarz. Der Quarzoszillator schwingt dann etwas oberhalb seiner Serienresonanz aber unterhalb der Antiresonanzfrequenz. Die hohe Frequenzstabilität des Oszillators und die Kreisgüte werden weiterhin vom Quarz bestimmt.

Ist der Quarz mit der Ziehkapazität in Reihe geschaltet, erscheint die Lastresonanz von der Serienresonanz in Richtung der Parallelresonanz verschoben. Mit parallel geschalteter Ziehkapazität bleibt die Serienresonanz des Quarzes unverändert. Die Parallelresonanzstelle wird zur Lastresonanzfrequenz in Richtung der Serienresonanzstelle verschoben.

Parallelresonanz

In der Literatur wird die Ortskurve eines Quarzresonators vielfach auch zur reellen Achse nicht symmetrisch dargestellt und ist dann in den 4. Quadranten nach unten verschoben. Mit den weiter oben hergeleiteten Bestimmungsgleichungen für die Real- und Imaginärkomponente konnte auch mit unterschiedlichen Parametervorgaben keine entsprechende Darstellung erreicht werden.

In den verschoben gezeigten Darstellungen der Literatur endet der Impedanzzeiger im Ortskurvendiagramm am rechten Ende des Kreisdurchmessers und bestimmt die Parallelresonanz fp. Der Zeiger weist einen kapazitiven Anteil aus. Der Quarz zeigt dort kapazitives Verhalten und diese Frequenz ist in keiner Quarzoszillatorschaltung nutzbar. Der Zeiger der Maximalimpedanz geht durch den Ortskreismittelpunkt und endet so bei einer noch höheren Frequenz.

Ortskurven in dieser Darstellung haben ebenfalls zwei Schnittpunkte mit der Re-Achse und φ=0°. Die niedrigere Frequenz wird Resonanzfrequenz fr genannt. Der dort reelle Impedanzwert ist der Resonanzwiderstand des Quarzes. Die höhere Frequenz mit reeller Impedanz ist die Antiresonanzfrequenz fa. Der Widerstandswert wird als Parallelwiderstand bezeichnet. Der Verlauf der Blindwiderstandskurve würde in diesem Fall einen ebenso fließenden Übergang zeigen wie an der Resonanzstelle.

Prinzipschaltungen mit Quarzresonatoren

Quarzresonatoren sind passive Bauelemente, deren Resonanzeigenschaften nur in aktiven Schaltungen nutzbar sind. Durch die Kombination der kristallmechanischen mit elektrischen Eigenschaften übertreffen sie hinsichtlich der Frequenzgenauigkeit und Güte die rein elektrischen Oszillatoren aus Spule und Kondensator bei Weitem. Quarzoszillatoren erzeugen präzise Referenzfrequenzen, eignen sich aber nicht direkt in kontinuierlich durchstimmbaren Frequenzgeneratoren.

Das folgende Bild zeigt den prinzipiellen Einsatz von Quarzresonatoren in Oszillatorschaltungen. Links ersetzt der Quarz in einem Colpitts-Oszillator die Spule. Die Kondensatoren C1 und C2 der Colpittsschaltung bilden mit der statischen Quarzkapazität C0 die Lastkapazität für den Quarz und ist mitbestimmend für die Resonanzfrequenz. Der Quarz verhält sich induktiv und schwingt auf einer Antiresonanzfrequenz fa, die etwas oberhalb seiner Serienresonanz liegt. Die Drossel L im Kollektorkreis verhindert den Signalkurzschluss zur Betriebsspannung. Das Oszillatorsignal wird am Kollektor abgenommen.

In der rechten Schaltung wirkt der Quarz als Serienresonanzkreis und liegt in der Signalrückkopplung vom Ausgang auf den Eingang. Im zweistufigen Verstärker arbeiten beide Transistoren in Emitterschaltung. Die Stufen sind galvanisch durch CK1 entkoppelt. Die Gesamtphasendrehung beträgt 360°. Der Quarz ist bei seiner Resonanzfrequenz sehr niederohmig. Aufgrund der Phasenbedingungen besteht eine Signalmitkopplung, wodurch die Schaltung zum Oszillator wird. Mit dem Trimmkondensator kann die Frequenz geringfügig nachgestellt (gezogen) werden. Die Oszillatorfrequenz wird über CK2 frei von Gleichspannung ausgekoppelt.