Kenndaten periodischer Signale
In der Elektronik gibt es viele periodische Signale, die keinen sinusförmigen Verlauf haben, sich aber eindeutig durch eine Reihe bestimmter Werte beschreiben lassen. Die Signalform ist durch ihren zeit- oder winkelabhängigen Verlauf gekennzeichnet. Einfache Signalformen sind durch ihre Namen gekennzeichnet, wie es die folgenden Beispiele zeigen.
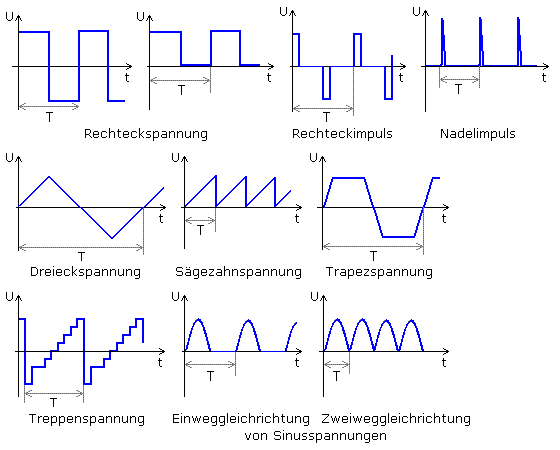
Periodendauer
Ein periodischer Signalverlauf wiederholt sich in gleicher zeitlich regelmäßiger Abfolge. Die Periodendauer ist die Zeit einer vollständigen Schwingung, die zur kompletten Signaldarstellung notwendig ist. Sie hat das Formelzeichen T mit der Maßeinheit s für Sekunde.
Frequenz
Die Frequenz eines periodischen Signals errechnet sich aus dem Kehrwert der Periodendauer. Der Formelbuchstabe ist f. Die Maßeinheit das Hertz in Hz = s−1.
Amplitude
Bei periodischen Signalen ist der Momentanwert der Signalamplitude innerhalb einer Periode nicht konstant. Zur Signalbeschreibung wird der Spitze-Tal-Wert, auch als Spitze-Spitze-Wert bekannt, uss oder iss benutzt. Verlaufen die Signale zur Nulllinie symmetrisch, können sie auch durch den einfachen Spitzenwert beschrieben werden. Das Formelzeichen wird mit dem Dachzeichen als û für us oder î anstelle von is gekennzeichnet.
Gleichwert oder arithmetischer Mittelwert
Der arithmetische Mittelwert eines periodischen Wechselsignals entspricht dem Flächeninhalt unter der Zeitfunktion einer ganzen Periode. Er errechnet sich praktisch aus der Summe aller Teilgrößen, dividiert durch die Anzahl der Teilwerte. Soll der Wert grafisch bestimmt werden, so unterteilt man bei periodischen Signalen den Zeitraum einer Periode in möglichst viele Teilabschnitte und bestimmt die zugehörigen Momentanwerte. Die Summe aller Momentanwerte unter Berücksichtigung ihrer Vorzeichen wird durch die Anzahl der Summanden geteilt.

Mathematisch wird die Fläche unter der Kurve für eine Periode durch Integration der Funktionsgleichung in den Grenzen von 0 bis T bestimmt. Das Ergebnis entspricht der DC, Gleichspannung/Gleichstrom-Komponente des Signals.
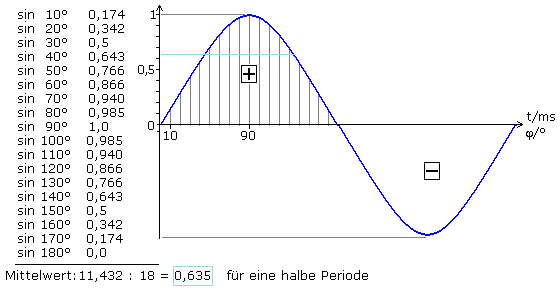
Das Bild zeigt ein zu null symmetrisches Sinussignal, dessen Gleichanteil nach der Summationsmethode für eine halbe Periode bestimmt wurde. Die zweite Halbperiode hat den gleichen aber negativen Summenwert. Ein periodisches, zur Nulllinie symmetrisches Signal hat folglich keinen Gleichanteil.
Nach DIN 40110 liegt eine Wechselgröße vor, wenn der arithmetische Mittelwert gleich null ist.
Ein Mischsignal kann immer in eine Wechselgröße und einen Gleichanteil zerlegt werden.
Gleichrichtwert
Der Gleichrichtwert eines Signals ist sein absoluter arithmetischer Mittelwert. Bei seiner Bestimmung werden nur die absoluten und damit vorzeichenlosen Beträge addiert und durch die Anzahl der Summanden dividiert. Der Gleichrichtwert des Signals steht für seine mittlere Gleichspannung oder den mittleren Gleichstrom. Er wird auch elektrolytischer Mittelwert genannt. Der Gleichrichtwert eines sinusförmigen Strom gibt an, welcher Gleichstromwert dieselbe Ladungsmenge im betrachteten Zeitraum transportiert.

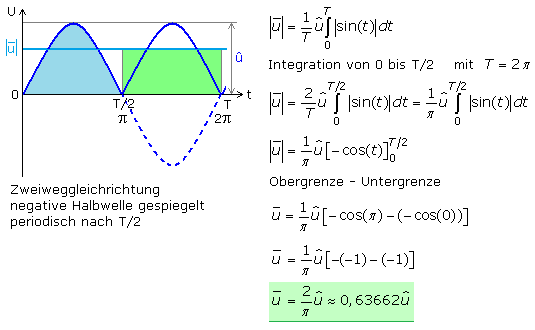
Die folgende Skizze zeigt die Herleitung des Gleichrichtwerts für eine sinusförmige Spannung mit der Periodendauer T = 2·π. Der hellblaue und grüne Flächeninhalt muss identisch sein. Bei der Zweiweggleichrichtung werden beide Sinushalbwellen berücksichtigt und das Ausgangssignal ist schon nach der halben Periodendauer periodisch. Bei der Einweggleichrichtung wird pro Periode nur der Flächeninhalt einer Sinushalbwelle erfasst, während er für die zweite Periodenhälfte null ist. Der Gleichrichtwert ist bei der Einweggleichrichtung einer Sinusgröße daher nur halb so groß.
Effektivwert
Der Effektiv- oder RMS-Wert (root mean square) ist der quadratische Mittelwert eines periodischen Signals. Er ist der leistungswirksame Wert eines periodischen Signals und direkt vergleichbar mit den Gleichgrößen von Spannung und Strom, die am ohmschen Widerstand die gleiche elektrische Energie und im zeitlichen Mittel dieselbe elektrische Leistung umsetzen. Als Formelzeichen U oder Ueff, wobei der Index meistens nicht geschrieben wird.
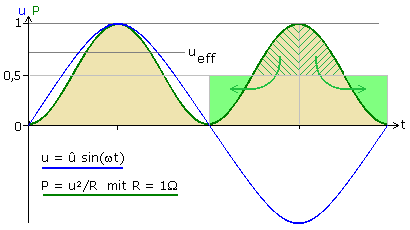
Die elektrische Leistung ist das Produkt aus Spannung und Strom. Im Zeitdiagramm verläuft die Leistungskurve für symmetrische Sinuskurven von Spannung und Strom nur im positiven Bereich und hat die doppelte Frequenz. Mathematisch errechnet sich der Effektivwert aus der Quadratwurzel des Mittelwerts der Leistungskurve über eine Periode. Der Effektivwert ist vom Scheitelwert und von der Kurvenform abhängig.
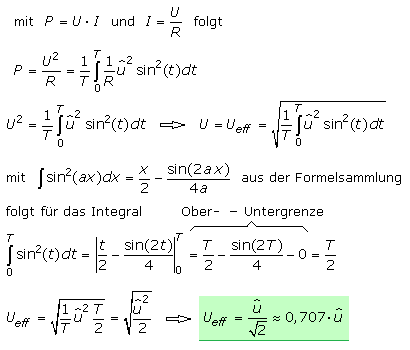
Der Wert kann auch grafisch durch die Methode des Auszählens der Flächen bestimmt werden. Aus dem so bestimmten Wert wird die Quadratwurzel gezogen. Die folgenden Bilder zeigen Beispiele zur Ermittlung des Effektivwertes nichtsinusförmiger periodischer Signale.
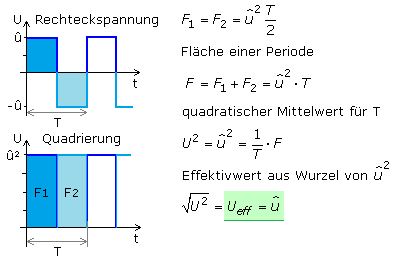
Für ein zur Nullachse symmetrisches Rechtecksignal erhält man das Ergebnis auch durch folgende Überlegung. Der Signalverlauf der ersten Halbperiode ist vergleichbar mit einer Gleichspannung der Größe +û. Die zweite Halbperiode entspricht einer Gleichspannung mit dem Wert −û. Für die am Wirkwiderstand umgesetzte Leistung ist die Polarität der Spannung und des daraus resultierenden Stromes gleichgültig. Bei diesem Rechtecksignal liegt immer der absolute Spannungswert û an. Dieser Wert ist gleich dem hergeleiteten Effektivwert.
Das folgende Beispiel einer Rechteck-Mischspannung liefert den gleichen Effektivwert wie eine zur Nullachse symmetrische Sinusspannung. Ein Multimeter im AC-Messbereich zeigt einen abweichenden Wert an, da die Skalen der meisten Messgeräte nur für Effektivwerte sinusförmiger Signale geeicht sind.
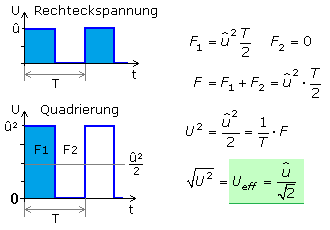
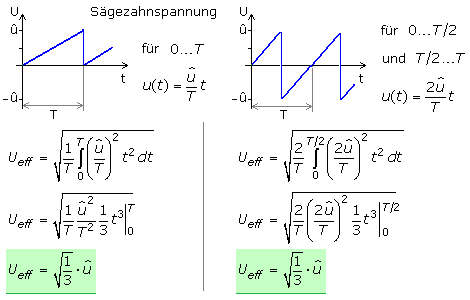
Ein dreieckförmiges Signal kann in einzelne Funktionsabschnitte mit positiver und negativer Steigung unterteilt werden. Beim zeitsymmetrischen Dreieck sind die einzelnen Flächenteile gleich. Das ist aus dem Kurvenverlauf erkennbar, kann aber auch durch die bestimmten Integrale gezeigt werden. Zur Berechnung des Effektivwerts genügt es daher über den ersten Kurvenabschnitt zu integrieren und mit 4 zu multiplizieren.
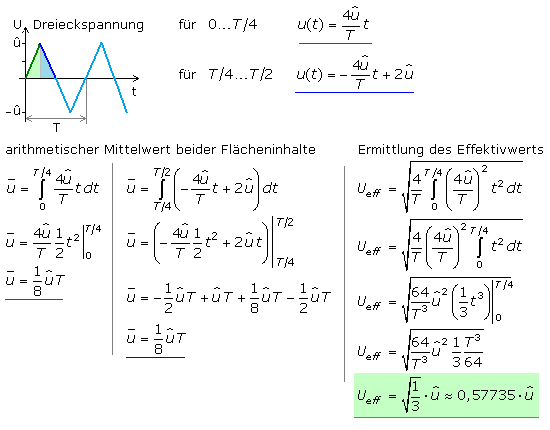
Die folgenden Herleitungen zeigen, dass die Effektivspannung für Sägezahnsignale identisch mit der für Dreiecksignale ist.
Scheitelfaktor oder Crestfaktor
Das Verhältnis des Spitzenwerts zum Effektivwert eines Signals wird als Scheitelfaktor oder Crestfaktor bezeichnet und hat das Formelzeichen ξ (xi, griechischer Kleinbuchstabe). Der Faktor wird von der Signalform bestimmt und ist größer oder gleich 1. Bei Sinussignalen hat der Scheitelfaktor den Wert √2 = 1,414. Ein Dreiecksignal hat den Crestfaktor √3 = 1,73 und ein symmetrisches Rechtecksignal den Wert 1.
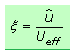
Formfaktor
Dreheisenmessgeräte zeigen stets den richtigen Effektivwert einer Wechselgröße an, sind aber nur für niedrige Frequenzen geeignet. Drehspulmessgeräte mit Messgleichrichter wurden ursprünglich für die Anzeige des Effektivwerts rein sinusförmiger Größen geeicht. Sie erfassen den Gleichrichtwert oder Betragsmittelwert des Signals und beziehen einen Formfaktor mit ein. Der Formfaktor ist von der Kurvenform abhängig und das Messgerät kann nur die Kurvenform richtig anzeigen, auf die es geeicht ist.
Der Formfaktor F ist das Verhältnis zwischen Effektivwert und Gleichrichtwert. Der Wert für Sinusgrößen beträgt F = 1,11. Beim symmetrischen Rechtecksignal ist F = 1 und das Signal einer Sinus-Einweggleichrichtung liefert F = 1,571. Messgeräte mit elektronischen Rechenschaltungen können aus unterschiedlichen Signalen den Effektivwert ermitteln und somit den Messwert signalunabhängig richtig anzeigen.
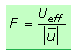
Impulsgrößen
Rechtecksignale und andere Impulse mit steilen Flanken erreichen ihre Maximalwerte nicht sogleich. Die Flankenanstiege verlaufen nicht rechtwinklig zur Zeitachse. Es vergehen bestimmte Zeiten, die am Oszillograph bei geeigneter Dehnung der Zeitachse darstellbar sind. Einige Parameter sind genormt und werden besonders benannt. Die folgende Skizze zeigt alle wichtigen Benennungen.
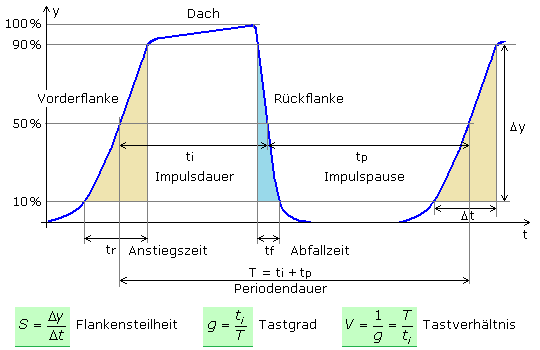
- Impulsdach
- Als Impulsdach wird der Bereich zwischen (90 ... 100)% der Maximalamplitude bezeichnet.
- Anstiegzeit
- Rise time tr ist die Zeitdifferenz der Vorderflanke gemessen von 10% ab dem absoluten Pulsboden bis 90% zum absoluten Pulsdach ohne Berücksichtigung möglicher Über- oder Unterschwingungen.
- Abfallzeit
- Fall time tf ist die Zeitdifferenz der Rückflanke zwischen 90% gemessen vom absoluten Pulsdach bis 10% gemessen zum absoluten Pulsdoden ohne Berücksichtigung möglicher Über- oder Unterschwingungen.
- Impulsdauer
- Pulszeit ti ist die Zeit zwischen Vorder- und Rückflanke bei 50% der Maximalamplitude.
- Tastgrad g
- Nach DIN IEC 469 ist es das Verhältnis von Impulsdauer ti zur Pulsperiodendauer T.
- Tastverhältnis V
- Es ist der Kehrwert des Tastgrads g und somit die Pulsperiodendauer dividiert durch Impulsdauer.
- Impulspausendauer
- Pausenzeit tp ist die Pulsperiodendauer abzüglich der Impulsdauer bei 50% der Maximalamplitude.
- Flankensteilheit S
- Sie ist das Verhältnis der Amplitudenänderung innerhalb einer Zeitspanne. Bei einem nichtlinearen Flankenverlauf werden die Bestimmungswerte zwischen 10% und 90% der Signalamplitude abgelesen. Ein positiver Wert bezeichnet die Vorderflanke. Eine negative Flankensteilheit steht für die Rückflanke.
- Abklingzeit
- ist die Zeit, die ein Spannungs- oder Strompuls benötigt, um auf 10% seines Maximalwerts abzunehmen. Die Abklingzeit ist ungefähr proportional zur Zeitkonstante eines Schaltkreises. In der Audiotechnik kennzeichnet sie als Reverberation Time die Nachhallzeit und ist von der Frequenz abhängig.