Äquivalente Stern-Dreieck-Umrechnungen

Nicht jedes Widerstandsnetzwerk besteht aus parallelen oder in Reihe liegenden Teilzweigen und kann durch einfaches Umzeichnen aufgelöst werden. Ein Hilfsmittel bietet die äquivalente Stern-Dreieck-Umwandlung. Beide Schaltungsvarianten gibt es in Generatorschaltungen der Stromnetze, in der Antriebstechnik mit leistungsstarken Elektromotoren und in Brückenschaltungen. Drei Widerstände als Dreieckschaltung angeordnet kann in eine dazu gleichwertige Sternschaltung umgewandelt werden. Ziel der Umwandlung ist es, dass die Verhältnisse zwischen den ausgewählten Klemmen in beiden Schaltungsvarianten gleich sind.

Dreieck zu Stern Umwandlung

Die drei Widerstände Rd1, Rd2 und Rd3 bilden eine Dreieckschaltung zwischen den Klemmen 1, 2 und 3. Die dazu äquivalente Sternschaltung hat die gleichen Klemmen und die zu bestimmenden Widerstände Rs1, Rs2 und Rs3. Die Spannung zwischen den Klemmen 1 und 2 der Dreieckschaltung muss gleich der Spannung der Sternschaltung zwischen den Klemmen 1 und 2 sein. Die Abfolge der Indexziffern gibt die Betrachtungsrichtung z. B. von 1 nach 2 an.

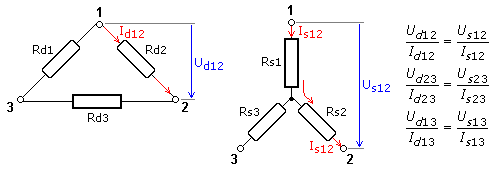
Für die Spannungen zwischen den gleichen Punkten gilt: \[{U_{d\,12}} = {U_{s\,12}}\quad {U_{d\,13}} = {U_{s\,13}}\quad {U_{d\,23}} = {U_{s\,23}}\] In der Dreieckschaltung fließt zwischen 2 Klemmen nur ein Strom, während er sich in der Sternschaltung im Sternpunkt aufteilt. Die Widerstandswerte der zueinander gleichwertigen Schaltungsvarianten sind daher nicht gleich. Für die Dreieckschaltung kann zwischen den Punkten 1 und 2 der wirksame Gesamtwiderstand bestimmt werden. Zum Widerstand Rd1 liegt die Summe der beiden anderen Widerstände parallel. Entsprechende sind die mathematischen Ansätze für den wirksamen Gesamtwiderstand zwischen den Klemmen 1 und 3 sowie 2 und 3: \[{R_{d\,12}} = {R_{d2}}||{R_{d1}} + {R_{d3}}\quad {R_{d12}} = \frac{{{R_{d2}}({R_{d1}} + {R_{d3}})}}{{{R_{d1}} + {R_{d2}} + {R_{d3}}}}\] \[{R_{d\,13}} = {R_{d1}}||{R_{d2}} + {R_{d3}}\quad {R_{d13}} = \frac{{{R_{d1}}({R_{d2}} + {R_{d3}})}}{{{R_{d1}} + {R_{d2}} + {R_{d3}}}}\] \[{R_{d\,23}} = {R_{d3}}||{R_{d1}} + {R_{d2}}\quad {R_{d23}} = \frac{{{R_{d3}}({R_{d1}} + {R_{d2}})}}{{{R_{d1}} + {R_{d2}} + {R_{d3}}}}\] In der Sternschaltung ist der gleichwertige Gesamtwiderstand zwischen den Klemmen gleich der Summe der beiden dort in Reihe geschalteten Widerstände: \[{R_{s\,12}} = {R_{s1}} + {R_{s2}}\] \[{R_{s\,13}} = {R_{s1}} + {R_{s3}}\] \[{R_{s\,23}} = {R_{s2}} + {R_{s3}}\]

Der Formelsatz für die äquivalente Umwandlung hat jeweils drei Gleichungen und drei Unbekannte. Die Widerstandswerte der Dreieckschaltung sind bekannt, gesucht sind die entsprechenden Widerstandswerte für die Sternschaltung. Die Formeln zwischen den gleichen Klemmen müssen gleich sein. Die Transformationsgleichungen sind in jeder guten Formelsammlung zu finden. Für einen Widerstandswert wird die schrittweise Herleitung durchgeführt. \[\begin{array}{l} {R_{s1}} + {R_{s2}} = \frac{{{R_{d2}}({R_{d1}} + {R_{d3}})}}{{{R_{d1}} + {R_{d2}} + {R_{d3}}}}\quad (I)\\ {R_{s1}} + {R_{s3}} = \frac{{{R_{d1}}({R_{d2}} + {R_{d3}})}}{{{R_{d1}} + {R_{d2}} + {R_{d3}}}}\quad (II)\\ {R_{s2}} + {R_{s3}} = \frac{{{R_{d3}}({R_{d1}} + {R_{d2}})}}{{{R_{d1}} + {R_{d2}} + {R_{d3}}}}\quad (III) \end{array}\] Von Gl.(I) wird Gl.(III) subtrahiert und zum Ergebnis Gl.(II) addiert: \[{R_{s1}} = \frac{{{R_{d2}}({R_{d1}} + {R_{d3}})}}{{{R_{d1}} + {R_{d2}} + {R_{d3}}}} - \frac{{{R_{d3}}({R_{d1}} + {R_{d2}})}}{{{R_{d1}} + {R_{d2}} + {R_{d3}}}} + \frac{{{R_{d1}}({R_{d2}} + {R_{d3}})}}{{{R_{d1}} + {R_{d2}} + {R_{d3}}}}\] Die Klammern werden aufgelöst und es wird vereinfacht zu: \[2\,{R_{s1}} = \frac{{2\,({R_{d1}}\,{R_{d2}})}}{{{R_{d1}} + {R_{d2}} + {R_{d3}}}}\quad \Rightarrow \quad {R_{s1}} = \frac{{({R_{d1}}\,{R_{d2}})}}{{{R_{d1}} + {R_{d2}} + {R_{d3}}}}\] Die beiden anderen Widerstände der Sternschaltung werden mithilfe der folgenden Formeln berechnet: \[{R_{s2}} = \frac{{({R_{d2}}\,{R_{d3}})}}{{{R_{d1}} + {R_{d2}} + {R_{d3}}}}\quad \quad {R_{s3}} = \frac{{({R_{d1}}\,{R_{d3}})}}{{{R_{d1}} + {R_{d2}} + {R_{d3}}}}\] Hat in der Dreieckschaltung jeder Widerstand den gleichen Wert, dann hat in der gleichwertigen Sternschaltung jeder Widerstand den dritten Teil davon.

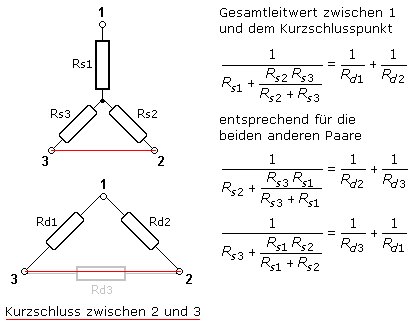
Ist keine Formelsammlung greifbar und möchte man sich die Formelumstellungen ersparen, dann können die Transformationsformeln auch nach folgendem Schema aufgestellt werden. Die Widerstände und die drei Klemmen sind eindeutig zu indizieren. Soll an der Klemme 1 der Sternwiderstand Rs1 berechnet werden, dann müssen die beiden an dieser Klemme 1 angeschlossenen Widerstände der Dreieckschaltung Rd1 mit Rd2 multipliziert werden und durch die Summe der drei Dreieckwiderstände dividiert werden. Für die beiden anderen Sternwiderstände gilt das mit der entsprechenden Indizierung.

Stern zu Dreieck Umwandlung

Die Transformation ist auch für eine dimensionierte Sternschaltung zur gleichwertigen Dreieckschaltung möglich. Die Formeln zur Äquivalentumwandlung sind in Formelsammlungen zu finden. Sie können ausgehend von den Formeln von oben hergeleitet werden.

Werden die Widerstandsverhältnisse der Sternschaltung mit den entsprechenden Verhältnissen der hergeleiteten Dreieckschaltung gleichgesetzt, so kürzen sich deren Nenner: \[\frac{{{R_{s1}}}}{{{R_{s2}}}} = \frac{{{R_{d1}}}}{{{R_{d3}}}}\quad \quad \frac{{{R_{s1}}}}{{{R_{s3}}}} = \frac{{{R_{d2}}}}{{{R_{d3}}}}\quad \quad \frac{{{R_{s2}}}}{{{R_{s3}}}} = \frac{{{R_{d2}}}}{{{R_{d1}}}}\] Die Dreieck zu Stern Transformationsformel für Rs1 wird durch den Zählerwert Rd2 dividiert und die Verhältnisse im Nenner werden durch mit den soeben aufgestellten Verhältnissen passend kombiniert: \[{R_{s1}} = \frac{{{R_{d1}}\,}}{{\frac{{{R_{d1}}}}{{{R_{d2}}}} + 1 + \frac{{{R_{d3}}}}{{{R_{d2}}}}}}\quad \Rightarrow \quad {R_{s1}} = \frac{{{R_{d1}}}}{{1 + \frac{{{R_{s3}}}}{{{R_{s2}}}} + \frac{{{R_{s3}}}}{{{R_{s1}}}}}}\] Es wird nach dem zu bestimmenden Rd1 umgestellt und der Klammerausdruck ausmultipliziert: \[{R_{d1}} = {R_{s1}}\left( {1 + \frac{{{R_{s3}}}}{{{R_{s2}}}} + \frac{{{R_{s3}}}}{{{R_{s1}}}}} \right) = {R_{s1}} + \frac{{{R_{s1}}\,{R_{s3}}}}{{{R_{s2}}}} + {R_{s3}}\] Die Bestimmungsformel für den gleichwertigen Dreieckswiderstand ist: \[{R_{d1}} = \frac{{{R_{s1}}\,{R_{s3}}}}{{{R_{s2}}}} + {R_{s1}} + {R_{s3}}\] Für die beiden anderen Dreieckswiderstände gilt mit entsprechender Indizierung: \[{R_{d2}} = \frac{{{R_{s1}}\,{R_{s2}}}}{{{R_{s3}}}} + {R_{s1}} + {R_{s2}}\quad \quad {R_{d3}} = \frac{{{R_{s2}}\,{R_{s3}}}}{{{R_{s1}}}} + {R_{s1}} + {R_{s3}}\] Hat in der Sternschaltung jeder Widerstand den gleichen Wert, dann hat in der gleichwertigen Dreieckschaltung jeder Widerstand den dreifachen Wert.

Anwendungsbeispiel – Widerstandsbrücke

Die Stern-Dreieck-Umwandlung soll am folgenden Netzwerk einer nicht abgeglichene Brückenschaltung mit realen Widerständen durchgeführt und der Gesamtwiderstandswert bestimmt werden. Der Brückenwiderstand bildet mit den dazu links liegenden Widerständen eine Dreieckschaltung. Sie wird in eine äquivalente Sternschaltung umgerechnet. Das Ergebnis ist dann ein leicht zu überschauendes Widerstandsnetzwerk.

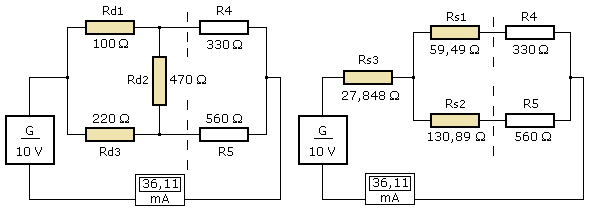
Nach der Umwandlung liegen die Widerstände Rs1 und R4 sowie Rs2 und R5 eine Reihenschaltung. Beide Reihenschaltungen bilden eine Parallelschaltung. Die beiden Ersatzwerte der Reihenschaltungen sind 389,5 Ω und 690,9 Ω. Der Wert der Parallelschaltung errechnet sich zu 249,1 Ω. Mit dem Reihenwiderstand Rs3 ergeben sich 276,9 Ω als Gesamtwiderstandswert. Die Simulation zeigt für beide Schaltungen identisches Verhalten.