Der RC-Tiefpass als Integrierer
Im Webprojekt wurde für einen passiven RC-Tiefpass die Ladekurve eines Kondensators aufgenommen und die Zeitkonstante tau (τ) der Schaltung bestimmt. Für sinusförmige Eingangssignale verschiedener Frequenzen wurden der Amplituden- und Phasengang für Tiefpässe beschrieben. Dieses Kapitel untersucht die Eigenschaften einiger RC-Tiefpässe mit ausgewählten Zeitkonstanten für besondere Eingangssignale konstanter Frequenz.
Das folgende Diagramm zeigt Simulationsergebnisse für RC-Tiefpässe mit umschaltbarer Zeitkonstante. Das Eingangssignal ist eine Rechteckspannung mit f = 1 kHz und dem Tastgrad von 0,5. Im Diagramm ist der Maßstab für die Ausgangsspannung (rechts) zur optimalen Darstellung angepasst.
RC-Tiefpass mit umschaltbarer Zeitkonstante:
| tau = 0,05 ms | tau = 0,1 ms |
| tau = 1 ms | tau = 5 ms |
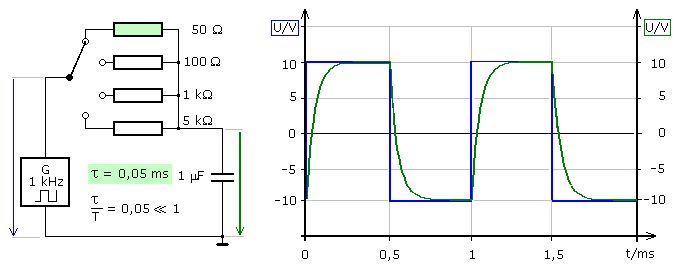
Es ist eine deutliche Abhängigkeit des Ausgangssignals von der Zeitkonstante der RC-Tiefpass Schaltung zu erkennen. Ist das Verhältnis \(\frac{\tau }{T} \ge 1\) so zeigt das Ausgangssignal eine annähernd lineare Ladekurve des Kondensators. Das rechteckförmige Eingangssignal wird in ein dreieckförmiges Ausgangssignal gewandelt. Je größer die Zeitkonstante bei konstanter Periodendauer ist, desto besser ist die Linearität des Ausgangssignals bei kleinerer Amplitude. Für Verhältnisse \(\frac{\tau }{T} \ll 1\) wird der Kondensator sehr schnell umgeladen und das Ausgangssignal ist dem Eingangssignal sehr ähnlich.
Bei einem Tiefpass ist die Grenzfrequenz umgekehrt proportional zu Zeitkonstante. Je größer die Zeitkonstante der Schaltung ist, desto kleiner ist die Amplitude des Ausgangssignals für eine bestimmte konstant gehaltene Eingangsfrequenz. Vergleichbare Ergebnisse gelten auch für einen RL-Tiefpass. Die Zeitkonstante errechnet sich dort aus dem Verhältnis \(\tau = \frac{L}{R}\) wobei das Ausgangssignal am Wirkwiderstand abgenommen wird.
Der Tiefpass zur mathematischen Integration
Ist die Funktion einer Kurve bekannt, dann kann durch die mathematische Integration die Fläche unter einem Kurvenabschnitt berechnet werden. Bei der grafisch aufwendigen Näherungsmethode wird die zu bestimmende Fläche in viele gleiche, möglichst schmale Rechtecke unterteilt. Die Summe aller Teilflächen ergibt die gesuchte Gesamtfläche, wobei die Genauigkeit mit der Zahl der Teilflächen steigt. Die Integration ist folglich die Summierung über unendlich viele schmale Teilflächen. Ein Tiefpass ist ein elektrisches Speicherglied, das bei richtiger Dimensionierung die Signalzeitflächen einer Eingangsgröße kontinuierlich summiert und so den Verlauf des Ausgangssignals bestimmt.
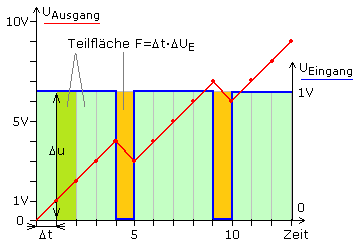
In der Darstellung wird die Eingangsspannung (blau) mithilfe gleicher Teilflächen zum Verlauf des roten Ausgangssignals integriert. Für jeden Zeitabschnitte ist Δt = 1. Die Spannungsänderung ist dabei immer die Differenz U = Uend − Uanf. Alle Teilflächen haben den gleichen absoluten Wert. Die grünen Flächen zählen positiv und die gelben Flächen negativ. Für das Ausgangssignal kann zu jedem Zeitpunkt die bis dahin erreichte Flächensumme und der dazu proportionale Spannungswert abgelesen werden.
Liegt an einem optimal dimensionierten Integrierglied mit \(\frac{\tau }{T} \gg 1\) eine Rechteck-, Sinus- oder Dreieckspannung, so zeigt das Ausgangssignal einen Dreieck-, Cosinus- bzw. Parabelverlauf. Umschaltbar dargestellt sind die Simulationsergebnisse für die beiden letzten Signale.
| Sinussignal | Dreiecksignal |
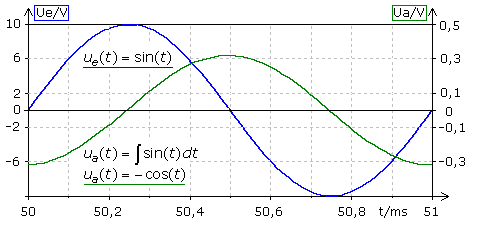
Der Kondensator symmetriert das Ausgangssignal zur Nulllinie. Für das Dreiecksignal ist der Vergleich mit der Mathematik leichter, wenn die parabelförmigen Halbbögen bei 50,5 ms getrennt und die farblich hervorgehobenen Abschnitte vom Extrempunkt zur Nulllinie verschoben werden. Die Integration der ebenfalls farblich gekennzeichneten Abschnitte des Dreiecksignals mit positiver und negativer Steigung ergibt die zugeordneten Parabelbögen entsprechend der mathematischen Integration.
Anwendungsbeispiele
In Netzteilen erfolgt nach der Gleichrichtung mithilfe von Integriergliedern eine Siebung und Glättung, um eine optimale Gleichspannung ohne AC-Anteile zu erhalten. In geregelten Verstärkerschaltungen und in der Regelungstechnik wird mit Integrierern eine Regelspannung erzeugt und der Einfluss kurzer Störimpulse auf den Regelkreis unterdrückt. In der Signaltechnik wird nach der Demodulation des hochfrequenten Eingangssignals mit Integriergliedern das niederfrequente Informationssignal ausgefiltert. In einigen Anwendungen arbeitet der Integrierer selbst als Demodulator.