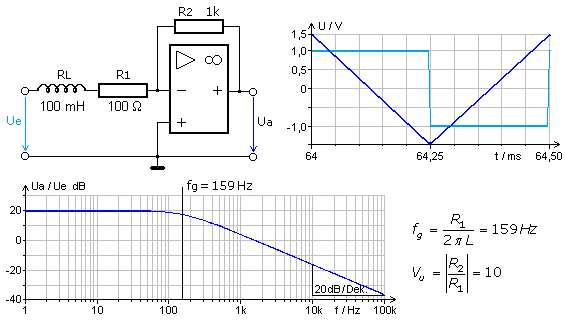
Integrierverstärker – Tiefpass mit OPV
Die Eigenschaften einer OPV-Schaltung werden von den externen Bauteilen bestimmt. Sind zusätzlich zu ohmschen Widerständen auch kapazitive und induktive Blindwiderstände wirksam, dann wird das Verhalten der Schaltung frequenzabhängig. Ein invertierender OPV mit einem Kondensator in der Gegenkopplung erfüllt die Grundschaltung des Integrierers oder Integrators. Als ideal angenommene Bauteile verhalten sich Kondensatoren und Spulen gegensätzlich. Ein Integrierer kann mit einem induktiven Blindwiderstand (Spule) im Eingangskreis und einem ohmschen Widerstand in der Gegenkopplung aufgebaut werden. Ein Integrierer entsteht auch mit einem kapazitiven Blindwiderstand (Kondensator) im Rückkoppelzweig und einem Wirkwiderstand am E− Eingang. Beide Varianten des Integrierers als aktiver Tiefpass sind in diesem Artikel beschrieben.
Das Bild zeigt die Schaltung eines aktiven Integrierers. Der zum Kondensator parallel geschaltete ohmsche Widerstand sorgt für eine stabile Arbeitsweise. Bei richtiger Dimensionierung beeinflusst er nicht die typischen Eigenschaften des Integrierers. Mit zunehmender Frequenz des Eingangssignals wird die Impedanz des Rückkoppelnetzwerks vom wesentlich kleineren Blindwiderstand der des Kondensators bestimmt.
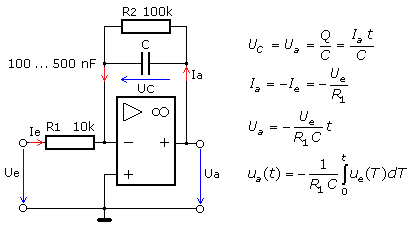
Ein Rechtecksignal kann als konstante Eingangsspannung Ue mit zeitlich wechselnder Polarität angesehen werden. In jedem Zeitabschnitt fließt durch den Eingangswiderstand R1 der konstante Strom Ie. Er lädt den Kondensator auf die Spannung UC auf, die der Ausgangsspannung −Ua entspricht. Der Arbeitsbereich der Schaltung liegt innerhalb der beiden Betriebsspannungen des OPVs. Die Ausgangsspannung ändert sich proportional mit der Zeit, die von der Zeitkonstante τ = R1 · C und der Eingangsspannung abhängt.
Die Änderung der Ausgangsspannung ist für gleiche Zeitabschnitte konstant. Die Schaltung führt somit eine analoge Rechenoperation durch. Die Ausgangsspannung ist proportional zur Spannungs-Zeit-Fläche des Eingangssignals. Mathematisch wird die Fläche unter einer Kurve durch ihr bestimmtes Integral ermittelt.
Der Integrierer als Analogrechner
Die mathematische Integration einer Funktionsgleichung führt zur Funktion der nächsthöheren Ordnung. Diese mathematische Eigenschaft soll für einfache Eingangssignale für den oben dimensionierten Integrierer gezeigt werden. Für gleiche maximale Ausgangsamplituden wurde die Kapazität des Kondensators angepasst. Die Eingangsfrequenz betrug 100 Hz.
Ein zu null symmetrisches Rechtecksignal entspricht während seiner Puls- und Pausenzeit einer konstanten positiven oder negativen Gleichspannung. Die Funktion der nächsthöheren Ordnung ergibt einen linear steigenden oder fallenden Kurvenverlauf. Eine Rechteckspannung am Eingang wird durch Integration am Ausgang zur Dreieckspannung.
Eine sich zeitlich linear ändernde Eingangsspannung (mittleres Bild) wird zur nächsthöheren Ordnung integriert und zeigt einen parabelförmigen Kurvenverlauf. Die mathematische Integration der Sinusfunktion (rechtes Bild) führt zur negativen Kosinusfunktion.
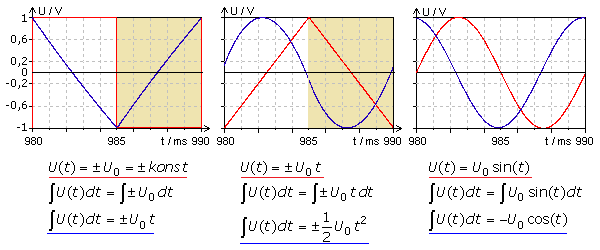
Verglichen mit den mathematischen Ergebnissen sind die Ausgangssignale in den Diagrammen invertiert, da der OPV in der Grundschaltung des Inverters arbeitet.
Der Integrierer als aktiver Tiefpass
Die Ausgangsspannung beim passiven RC-Tiefpass wird parallel zum Kondensator gemessen. Entsprechendes gilt für einen Integrator als TP 1. Ordnung mit dem kapazitiven Blindwiderstand in der Rückkopplung. Die Schaltung arbeitet präzise, solange der Aussteuerbereich des OPVs nicht überschritten wird und die von der Frequenz abhängige Leerlaufverstärkung ausreichend groß ist. Die blaue Kurve zeigt den Amplituden-Frequenzgang einer Simulationsschaltung mit dem LM 741 ohne einen zum Kondensator parallel geschalteten Rückkoppelwiderstand. Bei der grünen Kurve besteht die Rückkopplung aus der Parallelschaltung von R2 und C. Da der OPV in der Invertergrundschaltung arbeitet, beträgt im linearen Kurvenbereich der Phasenwinkel zwischen Ausgangs- und Eingangssignal +90°.
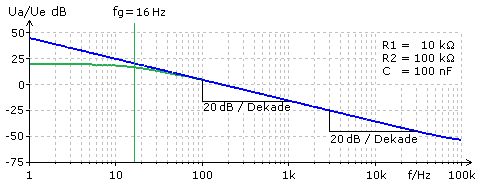
Die Kurvenverlauf zeigt, dass es sich um einen RC-Tiefpass 1. Ordnung handelt. Die Leerlaufverstärkung wird durch das Widerstandsverhältnis auf VU = −R2 / R1 herabgesetzt, wobei das Minuszeichen den Inverter kennzeichnet. Erst mit einem Rückkoppelwiderstand ist die Schaltung praktisch nutzbar, da sonst der OPV in einem übersteuerten Zustand verbleibt. Mit diesem Widerstand hat die Schaltung eine Grenzfrequenz, die durch R2 und C bestimmt ist. Der Arbeitsbereich des Integrierers als Analogrechner liegt oberhalb seiner Grenzfrequenz im linearen Kurvenbereich. Im Kapitel zur Impulsverformung mittels TP-Schaltungen sind diese Erkenntnisse dargelegt.
Ein Tiefpass mit der Eigenschaft τ / T » 1 wird als Integrierer bezeichnet.
Für den grünen Kurvenzug errechnet sich die Zeitkonstante des Tiefpasses aus τ = R2 · C = 0,01 s. Für Eingangssignale ab 100 Hz und der Periodendauer T = 0,01 s beginnt der lineare Kurvenverlauf, sodass Signale oberhalb dieser Frequenz mathematisch korrekt integriert werden. Erst aus der Herleitung der Übertragungsfunktion wird ersichtlich, dass die Grenzfrequenz fg des Integrierverstärkers nur durch den Rückkoppelwiderstand R2 und C bestimmt wird. Das Verhältnis der beiden ohmschen Widerstände bestimmt die maximale Grundverstärkung.

Unabhängig von R2 hat die Verstärkung des Ausgangssignals bei der Kreisfrequenz ωo = 1 / R1·C den Wert 1 oder 0 dB. Für die betrachtete Schaltung hat die Frequenz den Wert fo = 159,2 Hz. In der Übertragungsfunktion folgt auf den Verstärkungsfaktor VU des invertierenden OPVs ein Quotient, der aus der Herleitung der Übertragungsfunktion eines passiven RC-Tiefpass bekannt ist. Das Minuszeichen vor VU kennzeichnet den OPV als Inverter. Die Übertragungsfunktion kann als dynamische Gesamtverstärkung der Schaltung gesehen werden.
Der Integrierverstärker als RL-Tiefpass
Eine Integrierschaltung als aktiver RL-Tiefpass ist eher von theoretischem Interesse und wird praktisch nicht genutzt. In modernen Schaltungskonzepten wird der Einsatz von Spulen vermieden. Sie benötigen meist mehr Platz, sind aufwendiger in der Herstellung und halten bei geringerer Güte weniger präzise ihre Kenndaten ein. Die folgende Schaltung zeigt die Möglichkeit. Wie zuvor wird auch hier die Leerlaufverstärkung VU durch das absolute Verhältnis der ohmschen Widerstände bestimmt. Die Eingangsfrequenz des Rechtecksignals beträgt 2 kHz.