Binäre Block-Codices

In der Digitaltechnik wird mit diskreten Zählwerten gearbeitet. Damit die zu verarbeitenden Nachrichten von elektronischen Computersystemen verstanden werden, müssen sie erst nach einem definierten System codiert werden. Optimal wäre es Fehler, die bei der Datenverarbeitung auftreten können, rechtzeitig zu erkennen und vielleicht zu korrigieren. Die in Computersystemen ablaufenden Programme sind letztlich mathematisch logische Beschreibungen uns interessierender alltäglicher Probleme. Mathematik ist die Welt der Zahlen und in der Logik sind die zu vergleichenden Zustände wie gleich, größer oder kleiner diskret definiert. Wir sind es seit Langem gewohnt, mathematisch im Dezimalsystem zu denken. Ein elektronisches System kann dagegen optimal mit den beiden Zuständen 'Ein' und 'Aus' oder mathematisch 0 und 1 programmiert werden. An der Schnittstelle zwischen Mensch und Maschine ist daher eine Umcodierung der mathematischen Systeme sinnvoll.

Binärcode – Dualsystem

Das Dualsystem ist auf die beiden Zustände Ein und Aus, High und Low oder 0 und 1 reduziert. In geeigneter Kombination lassen sich damit alle denkbaren Operationen und Programme durch Computer ausführen. Die kleinste Einheit ist das 'binary digit' oder Bit. Vier Bits in Reihe geschrieben werden als Nibble oder Halb-Byte bezeichnet. Zwei Nibble in Reihe oder 8 Bit bilden ein Byte.

Mit einem Bit lassen sich genau zwei Zustände, stellvertretend durch die Dezimalziffern 0 und 1, darstellen. Das Dualsystem ist ein Stellenwertsystem zur Basis 2. Der Stellenwert nimmt zur höherwertigen Stelle von rechts nach links nach der Zweierpotenzreihe zu. Das Dual- und Dezimalsystem steht mathematisch in einfacher Beziehung. Der Dezimalwert einer Bitfolge errechnet sich als Summe aller Stellenwerte multipliziert mit dem jeweiligen gespeicherten Bit-Zustand 0 oder 1.

Wenn zum LSB, niederwertigen Bit (least significant Bit) eine 1 addiert wird, erhöht sich der Stellenwert einer gegebenen Dualzahl um 1. Da im Dualsystem nur 0 und 1 vorkommen, muss der Stellenwert 1 bei der Addition von 1 eine 0 ergeben und der folgende höhere Stellenwert um 1 erhöht werden. Dieser Übertrag ist identisch mit dem Additionsverfahren im Dezimalsystem beim Übergang von 9 nach 10.

Dualzahlen lassen sich addieren, wobei die Anzahl n der Bits den darstellbaren Wertebereich bestimmt. Mit einer 4-Bit Dualzahl sind 16 unterschiedliche Ganzzahlen darstellbar und bei 8 Bit sind es insgesamt 256 also 2ⁿ Zahlenwerte. In dieser Betrachtung kommen keine negativen Zahlen vor. Für ihre Darstellung muss der Zahlenbereich halbiert werden.

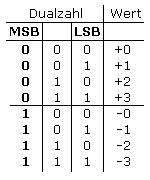
Mit dem links außenstehenden MSB, höchst wertigen Bit (most significant Bit), wird das Vorzeichen codiert. Mit MSB = 0 werden positive und mit MSB = 1 negative Zahlen gekennzeichnet. Für die zu codierende Zahl steht ein Bit weniger zur Verfügung.

Da mit dieser einfachen Methode der Wert 0 sowohl positiv als auch negativ auftritt, ist ein direkter mathematischer Vergleich auf 0 nicht möglich. Die Addition gibt nur innerhalb des positiven oder negativen Bereichs richtige Ergebnisse. Die Subtraktion als Addition einer negativen Dualzahl zu einer positiven Dualzahl liefert einen falschen Wert.

Das Zweierkomplement

Die Nachteile dieser negativen Dualzahldarstellung werden durch Bilden des Zweierkomplements verhindert. Der Wert null ist als positive Zahl definiert. Bei festgelegter Bit-Breite bildet man zuerst das Einerkomplement, indem man alle Bitwerte der Dualzahl invertiert. Das Zweierkomplement entsteht anschließend durch Addieren von binär 1 zum LSB. Die negativen Dualzahlen sind weiterhin am MSB = 1 zu erkennen. Die Doppeldarstellung der Null entfällt und Addition und Subtraktion sind im gegebenen Wertebereich fehlerfrei möglich.

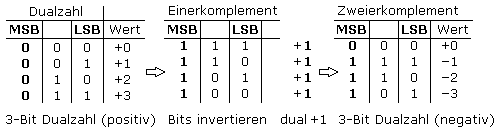
Eine negative Dualzahl kann durch Inversion aller Bits und anschließender Addition von dual 1 in ihre positive Dualzahl umgewandelt werden. In einem anderen Kapitel werden einfache Rechenoperationen mit Dualzahlen näher beschrieben.

BCD-Code

Die Codebezeichnung BCD steht für binary coded decimal und wird in der Informatik auch als 8-4-2-1 Code oder dual codierte Dezimalziffer bezeichnet. Um die Dezimalziffern 0 ... 9 im Dualsystem darzustellen, sind vier Bits oder eine Tetrade notwendig. Von den 16 unterschiedlichen Tetraden werden zur Codierung der Dezimalziffern nur die ersten 10 benötigt. Die verbleibenden 6 Tetraden, die nicht auftreten oder genutzt werden dürfen, werden als Pseudotetraden bezeichnet. Zur Darstellung einer n-stelligen Dezimalzahl sind im BCD-Code n Tetraden notwendig.

Der BCD-Code ist nicht identisch mit dem BCD-Zählcode, wo jede Stelle die Wertigkeit 1 hat und der Zahlenwert durch eine Reihe entsprechend gesetzter 1 Bits dargestellt wird. Noch nicht benötigte höhere Bits werden mit 0 aufgefüllt.

Der Binärcode einer Dezimalzahl >9 ist nicht identisch mit dem BCD-Code der Dezimalzahl.
Binär codiert: (27)10 = (00011011)2 und im BCD-Code: (0010 0111)BCD

Im BCD-Code kann jede Tetrade nur eine Dezimalziffer aus dem Wertebereich 0 bis 9 codieren. Die Bezeichnung 8-4-2-1-Code steht für die Wertigkeit der einzelnen Bits. Der BCD-Code ist daher ein gewichteter Code, wo jeder Bitstelle ein eigenes definiertes Gewicht oder Wertigkeit hat. Der Dezimalwert ist die Summe der einzelnen Dualziffern (0, 1) multipliziert mit der Wertigkeit des Bits. Dezimalzahlen mit n Stellen werden im BCD-Code durch eine Serie von n Tetraden geschrieben. Mit vier Tetraden in Serie ist der Dezimalzahlbereich von 0 ... 9999 im 8-4-2-1-Code binär darstellbar. Das Zeitsignal des DCF77-Senders ist BCD codiert und der BCD-Code wird auch zur Ansteuerung von LCD- und LED-Zahlendisplays genutzt. In der Computerarithmetik hat der BCD-Code an Bedeutung verloren.

Additionsverfahren

Ist das Ergebnis der bitweisen Addition eine Pseudotetrade, muss der dezimale Ergänzungswert 6 als binär 0110 addiert werden. Kommt es bei der Addition nur zum Übertrag (Carrybit) in die fünfte Stelle, steht das Bit an der Stelle des LSB der nächsthöheren Tetrade. Kann das Rechenwerk nur eine Tetrade darstellen, dann ist das angezeigte Ergebnis falsch, da der darstellbare Zahlenbereich überschritten wurde.

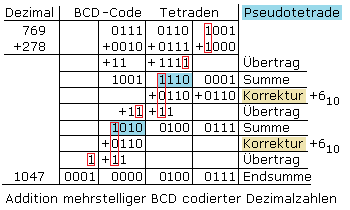
Setzt sich der BCD-Code aus mehreren Tetraden zusammen, so wird von rechts nach links tetradenweise addiert. Entsteht eine Pseudotetrade, so ist sie mit binär 0110 zur folgenden höheren Tetrade zu ergänzen. Kommt es wie beim rechten Tetradenpaar nur zum Übertrag in die fünfte Stelle, muss ebenfalls zur Summe binär 0110 addiert werden. Der Übertrag (rot) wird mit dem folgenden Tetradenpaar verrechnet. Ergibt die Summe eine Pseudotetrade wie in der Mitte und links, so muss ebenfalls mit binär 0110 additiv korrigiert werden. Der Übertrag (rot) in die fünfte Stelle wird in der folgenden Tetrade verrechnet.

Subtraktionsverfahren

Man kann im Dezimalsystem die Subtraktion durch die Addition des Zehnerkomplements der abzuziehenden Zahl, dem Subtrahenden ersetzen. Der Übertrag in die höhere Dekade wird verworfen. Dem Zehnerkomplement entspricht binär das Zweierkomplement. Man bildet es durch Invertieren aller Bits und addiert zum LSB eine 1. Die Subtraktion wird als bitweise Addition ausgeführt.

Zum Minuenden wird das Zweierkomplement des Subtrahenden addiert. Ist das Ergebnis eine Pseudotetrade, muss binär 0110 als dezimaler Korrekturwert +6 addiert werden. Entsteht bei der Addition ein Übertrag in die fünfte Stelle, dann ist das Ergebnis positiv. Bei einem Übertrag ohne Pseudotetrade muss ebenfalls mit binär 0110 additiv korrigiert werden. Das Endergebnis ist der Dezimalwert der Tetrade, wobei der Übertrag verworfen wird.

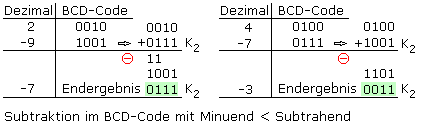
Ist der Subtrahend größer als der Minuend, dann ist das dezimale Ergebnis negativ. Die Subtraktion wird ebenfalls durch die Addition des Zweierkomplements des Subtrahenden ersetzt. Charakteristisch für ein negatives Ergebnis ist das Fehlen des Übertrags in die fünfte Stelle. Das Endergebnis ergibt sich aus dem Zweierkomplement der letzten Summe.

Exzeß-3-Code

Der Exzeß-3-Code ist ein weiterer in Tetraden organisierter Code und ein Zuordnungscode für Dezimalzahlen. Er wird auch Stibitz-Code nach seinem Entwickler genannt. Er baute 1937 eine mit Relais arbeitende Rechenmaschine, die im Dualsystem addieren konnte.

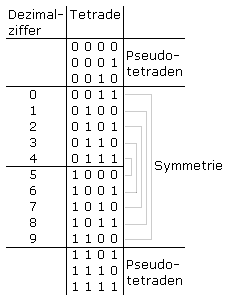
Beim Exzeß-3-Code sind die ersten und letzten drei Tetraden nicht genutzte Pseudotetraden. Da mit den mittleren 10 Tetraden die Dezimalziffern 0 ... 9 codiert sind, ist das Bitmuster jeder Tetrade um binär 3 größer als bei direkter Binärcodierung. Der BCD-Exzeß-3-Code ist ein symmetrischer Code.

Im Exzeß-3-Code werden die Tetraden 0000 und 1111 nicht genutzt. Eine Verwechslung mit einem Ausfall '0' als 0 Volt oder '1' für die Betriebsspannung ist nicht gegeben.

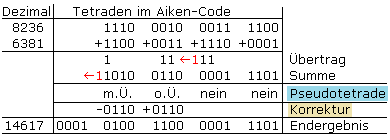
Kommt es bei der binären Addition zum Übertrag in die folgende höhere Tetrade, dann entsteht auch in der dezimalen Addition der Zehnerübertrag. Zu jeder Tetrade ist dann binär 0011 für dezimal 3 zu addieren. Ohne Übertrag muss das Zweierkomplement K2 binär 1101 für dezimal −3 addiert werden. Das folgende Bild zeigt für beide das Rechenschema.

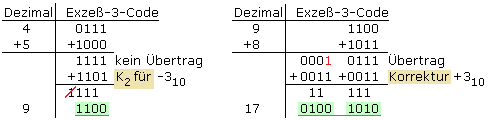
Auch im Exzeß-3-Code wird die Subtraktion durch Addition des Zweierkomplements ersetzt. Entsteht ein Übertrag in die fünfte Stelle, so wird er vernachlässigt, und zur Tetrade der Korrekturwert binär 0011 addiert.

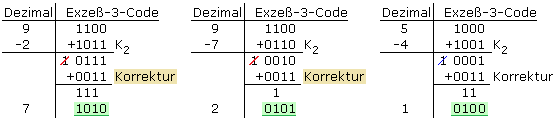
Das Ergebnis ist negativ, wenn der Subtrahend größer als der Minuend ist. Die Subtraktion wird wieder durch die Addition des Zweierkomplements des Subtrahenden durchgeführt. Da hierbei kein Übertrag in die fünfte Stelle entsteht, ist das Ergebnis als negativ gekennzeichnet. Es wird der Korrekturwert binär 1101 für dezimal −3 addiert. Ein hierbei auftretender Übertrag in die fünfte Stelle bleibt unbeachtet. Das Zweierkomplement der Tetrade ist der im Exzeß-3-Code vorliegende vorzeichenlose Dezimalwert.

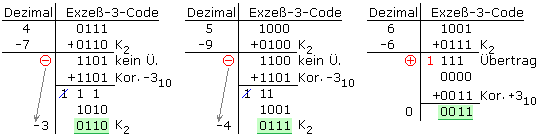
Sind Subtrahend und Minuend gleich, dann ist das Ergebnis dezimal 0. Die Addition des Zweierkomplements ergibt schon jetzt einen Übertrag in die fünfte Stelle. Die Subtraktion muss daher zu einem positiven Endergebnis führen. Da es sich um eine Subtraktion handelt, wird nur die Tetrade nicht aber der Übertrag additiv mit binär 0011 für dezimal +3 korrigiert.

Aiken-Code

Der Aiken-Code ist für die Dezimalziffern 0 ... 9 ein symmetrischer Code, bei dem die ersten und letzten fünf Tetraden genutzt werden. Die mittleren sechs Tetraden sind Pseudotetraden. Von links nach rechts gelesen hat jede Bitstelle eine feste Wertigkeit. Der Aiken-Code ist ein gewichteter Code und wird auch als 2-4-2-1-Code bezeichnet.

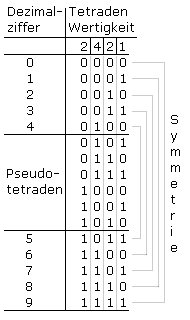
Die Binärdarstellung des Neunerkomplements der Dezimalzahlen erfolgt durch bitweises Invertieren. Bei ungeraden Dezimalziffern ist die letzte Binärstelle eine 1 und bei geraden Dezimalziffern immer eine 0. Das MSB hat für die Dezimalziffern 0 ... 4 eine 0 und für 5 ... 9 eine 1.

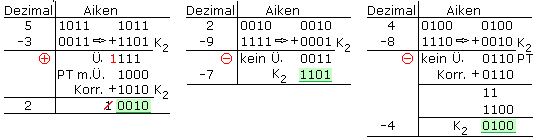
Der Aiken-Code eignet sich zur Addition und Subtraktion. Entsteht bei der Addition zweier Tetraden keine Pseudotetrade, muss nicht korrigiert werden. Ist das Ergebnis eine Pseudotetrade ohne Übertrag in die fünfte Stelle, dann muss binär 0110 für dezimal 6 addiert werden. Bei einer Pseudotetrade als Additionsergebnis mit Übertrag muss binär 0110 subtrahiert oder das entsprechende Zweierkomplement 1010 addiert werden.

Die Subtraktion erfolgt durch Addition des Zweierkomplements K2 des Subtrahenden. Ist der Subtrahend kleiner als der Minuend, so entsteht ein Übertrag in die fünfte Stelle. Tritt eine Pseudotetrade PT auf, muss korrigiert werden. Der positive Dezimalwert der Tetrade ist das gesuchte Ergebnis. Ist der Subtrahend größer als der Minuend, entsteht bei der Addition kein Übertrag, und das Ergebnis ist negativ gekennzeichnet. Falls eine Pseudotetrade entsteht, muss noch binär 0110 addiert werden. Das Endergebnis ist der negative Dezimalwert des Zweierkomplements der Tetrade.

Gray-Code

Der Gray-Code kann auch als Tetraden-Code auftreten. Es gibt ihn in unterschiedlichen Versionen, die eigentlich nie für arithmetische Zwecke genutzt werden. Allen gemeinsam ist ihre Einschrittigkeit, da sich zur Nachbartetrade immer nur eine Bitstelle ändert. Der Gray-Code findet Anwendung bei der Analog-Digital-Wandlung, in der Maschinensteuerung und bei der Messwertabtastung. Hier ist die Einschrittigkeit besonders wichtig, damit bei nicht optimal justierten mechanischen oder optischen Abtastsystemen oder Laufzeitunterschieden im System keine Zwischenwerte auftreten. Der Gray-Code wird zur Fehlerkorrektur in digitalen Übertragungssystemen eingesetzt.

Der klassische Gray-Code umfasst 10 Tetraden und ist nicht zyklisch. Der Glixon-Code ist ein modifizierter Gray-Code, der sich schon bei 10 Tetraden zyklisch verhält. Der Gray-Code auf 16 Tetraden erweitert ist zyklisch. Wird er als dezimaler Gray-Code, auch als Gray-Exzeß-3-Code bezeichnet, dann stellen die ersten und letzten drei Tetraden Pseudotetraden dar. Die Einschrittigkeit ist auch bei dieser Dezimalzahlcodierung gegeben.

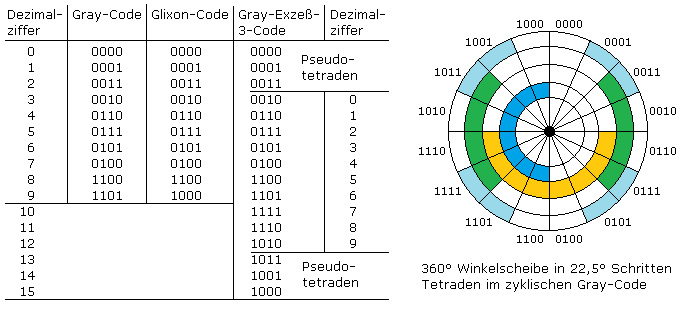
Bitmuster im Gray-Code

Die Konstruktionsregel, um die Bitmuster eines n-Bit Datenworts in vertikaler Abfolge fehlerfrei zu schreiben ist bekannt. Für den Gray-Code gibt es auch eine leicht zu behaltende Regel. Man beginnt mit einem 1-Bit-Datenwort und schreibt die beiden Zustände 0 und 1 untereinander.

Die Kombinationen für ein 2-Bit-Datenwort ergeben sich daraus durch Spiegelung des 1-Bit-Datenworts an der Horizontalen (rot). Man schreibt noch die Bitmuster des 1-Bit-Datenworts symmetrisch zur Spiegelachse davor und ergänzt nach oben mit 0 und nach unten mit 1.

Die Bitkombinationen für 3-Bit-Datenworte entstehen durch Spiegeln der 2-Bit-Kombinationen, dem symmetrischen Vorsetzen der 1-Bit-Kombinationen und dem Ergänzen mit 0 Werten nach oben und 1 Werten nach unten. Das Schema kann auf die Kombinationen aller n-Bit Datenworte im Gray-Code erweitert werden.

Code-Eigenschaften

Die verschiedenen Codices zeichnen sich durch bestimmte Eigenschaften aus. Einige der Wichtigen werden nachfolgend kurz beschrieben.

Stellenzahl: Der Binärcode ermöglicht mit zwei Zuständen 2ⁿ Codierungen. Darin ist n die Stellenzahl als Anzahl der Bits, die zur Codierung einer gegebenen Datenmenge notwendig ist. Die Stellenzahl entspricht der Informationsbreite des verwendeten Codes. Bei 20 unterschiedlichen Daten ist eine Bit-Breite von 2⁵, also n = 5 notwendig, wobei nicht alle Codeworte genutzt werden.
Nachrichtenmenge: Die maximal darstellbare Nachrichtenmenge M folgt aus der Zahl der unterscheidbaren Codeworte, die von der Bit-Stellenzahl n abhängt. Beim Binärcode gilt M = 2ⁿ. Mit der Stellenzahl einer Tetrade n = 4 lassen sich maximal 16 unterschiedliche Nachrichten codieren.
Gleichmäßigkeit: Wird die Menge der darzustellenden Nachrichten mit der gleichen Stellenzahl codiert, dann handelt es sich um einen gleichmäßigen Code.
Vollständigkeit: Werden zur Darstellung einer Nachrichtenmenge N alle Bitkombinationen des Codes benötigt, dann ist M, die maximale Nachrichtenmenge gleich N und man bezeichnet den Code als vollständig.
Redundanz: Redundanz entsteht, wenn die darzustellende Nachrichtenmenge N kleiner ist als die mit der gegebenen Stellenzahl maximal codierbaren Nachrichtenmenge M. Es existieren mehr Bitmuster als tatsächlich genutzt werden. Die Redundanz R ist die Differenz zwischen der maximal möglichen Datenmenge M bei der maximalen Stellenzahl m und der bestehenden Datenmenge N mit der dazu notwendigen Stellenzahl n. R = m − lb(N) mit lb als binärer Logarithmus. Werden die Dezimalziffern 0 ... 9 in einer Tetrade dargestellt, bleiben 6 Bitkombinationen ungenutzt. Es errechnet sich eine Redundanz von R = 0,68 Bits, denn zur Darstellung der Datenmenge wären 3,3 Bits ausreichend gewesen.
Stellendistanz: Die Stellendistanz d gibt die Anzahl der Binärstellen an, in denen sich zwei Nutzworte mit gleich langem Code voneinander unterscheiden. Mit der Stellendistanz lassen sich Aussagen zu Übertragungsfehlern machen. Bei fehlerfreiem Empfang ist die Stellendistanz null. Die Binärcodierung der Dezimalziffern weist ganz unterschiedliche Stellendistanzen auf.
Hammingdistanz: Die Hammingdistanz h ist die geringste paarweise Stellendistanz zwischen allen Nutzworten eines Codes gleicher Länge. Zwischen Stellen- und Hammingdistanz besteht der Zusammenhang: d ≥ h. Im Gray-Code ist die Hammingdistanz h = 1. Die Hammingdistanz kann bitweise mittels der XOR-Funktion bestimmt werden. Sie ist dann die Summe der Einsen.
Einschrittigkeit: Ein stetiger Code mit der Hammingdistanz h = 1 wird einschrittig genannt. Bei der Binärcodierung dürfen sich wie im Gray-Code zwei beliebige benachbarte Codeworte nur in einer einzigen Bitposition unterscheiden.
Eindeutigkeit: Ein Code ist eindeutig, wenn jedem Element der zu codierenden Nachrichtenmenge genau ein Element aus der Datenmenge gleich langer Codeworte zugeordnet ist.