KV-Diagramme

Edward Veitch entwickelte 1952 ein grafisches Verfahren zur Optimierung digitaler Schaltfunktionen. Es wurde ein Jahr später von Maurice Karnaugh erweitert und wird als Karnaugh-Veitch-Diagramm, kurz KV-Diagramm bezeichnet. Das KV-Diagramm hat zu allen logischen Kombinationen der Eingangsvariablen je ein Feld. Bei n Eingangsvariablen gibt es 2ⁿ Felder.

Bei der digitalen Schaltungssynthese wird aus der Wahrheitstabelle die Funktionsgleichung als disjunktive oder konjunktive Normalform erstellt. Die direkte Umsetzung führt fast immer zu einer aufwendigen Digitalschaltung. Mit den De Morganschen Gesetzen und der Schaltalgebra lassen sich optimierte und meist minimierte Funktionsgleichungen finden. Die KV-Diagramme vereinfachen die Optimierung und reduzieren die mathematischen Umrechnungen.

KV-Diagramm für zwei Eingangsvariable

Das folgende Bild zeigt den Zusammenhang zwischen der Wahrheitstafel und dem KV-Diagramm. Jeder Platz entspricht einer schaltalgebraischen Gleichung. In ihr kommt jede Variable in der normalen und negierten Form je einmal vorkommt. Anstelle der Gleichungen schreibt man die Variablen an die Ränder des KV-Diagramms und erhält ein koordinatives Zuordnungssystem. Die Variablennamen können in den Spalten der Wahrheitstabelle anders eingeordnet sein. Die Randbezeichnungen des KV-Diagramms ändern sich entsprechend. Die ermittelbare Funktionsgleichung bleibt davon unbeeinflusst.

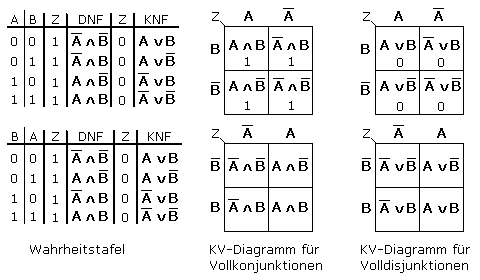
Jedes Feld ist durch seine Zeilen- und Spaltenvariable eindeutig bestimmt. Ist die optimierte DNF gesucht, dann werden die Minterme mit den Feldwerten 1 betrachtet. Die Variablen sind durch UND verknüpft. Die Einzelverknüpfungen sind durch ODER verbunden. Ist die optimierte KNF gesucht, dann werden Maxterme mit den Feldwerten 0 betrachtet, deren Variablen sind dann durch ODER zu verknüpfen, während die Einzelterme durch UND verbunden werden.

KV-Diagramm für drei Eingangsvariable

Bei drei Eingangsvariablen mit je zwei logischen Schaltzuständen sind acht Felder im KV-Diagramm zu bezeichnen. Die Wahrheitstafel zeigt Minterme mit logischem Ausgang 1. Sie werden nach den oben genannten Regeln in das KV-Diagramm übertragen.

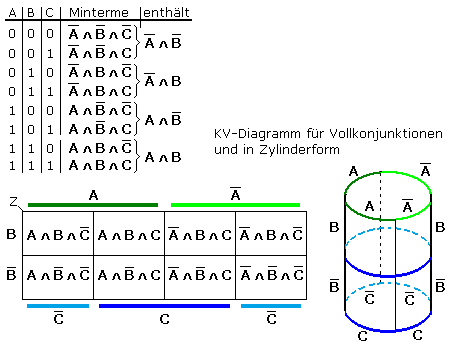
KV-Diagramm für vier Eingangsvariable

Bei vier Eingangsvariablen besitzt das KV-Diagramm 16 Felder. Die Variablen sind so am Rand zu verteilen, dass sich ungleiche Variablen nicht gegenseitig überschneiden und gleiche Variablennamen paarweise normal und negiert nebeneinander auftreten. Die ebene Darstellung des KV-Diagramms ist über die Diagonalen verbunden als Kugel zu sehen.

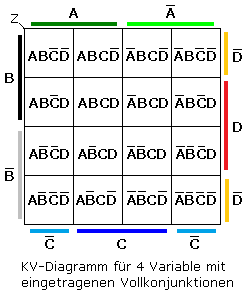
Ab fünf Variablen lassen sich KV-Diagramme nicht mehr in einer Ebene darstellen. Sie bilden Quader mit übereinander liegenden Ebenen. Zur besseren Übersicht werden sie nach rechts abgebaut und nebeneinander gelegt. In allen Fällen sind beim Erstellen der KV-Diagramme folgende Regeln zu beachten:

• An jeder Kante steht nur eine Variable in normaler und negierter Form.
• Bei mehr als zwei Variablen müssen gegenüberliegende Kanten unterschiedlich aufgeteilt sein.
• Gegenüberliegende Kanten sind als benachbart anzusehen.

Herleiten der Funktionsgleichung aus dem KV-Diagramm

Aus der Wahrheitstabelle folgt die Funktionsgleichung entweder durch Herausschreiben der disjunktiven oder konjunktiven Normalform. Ein KV-Diagramm ist eine andere Darstellung der Wahrheitstabelle. Lassen sich die 1-Zustände der Minterme oder 0-Zustände der Maxterme durch besondere Blockbildung zusammenfassen, dann ergeben sich bereits minimierte Funktionsgleichungen. Das erspart eine meist langwierige Optimierung der DNF oder KNF mithilfe der Schaltalgebra. Bei der Blockbildung sind einige Regeln zu beachten:

• Blöcke können nur horizontal, vertikal oder quadratisch auftreten.
• Eine Blockbildung kann nur für Minterme oder Maxterme gebildet werden.
• Die Anzahl der Felder im Block entspricht einer 2-er Potenz, also 2, 4, 8, 16.
• Blöcke sollten so groß als möglich sein. Sie dürfen sich überschneiden.

Beispiele zur Blockbildung

Im KV-Diagramm lassen sich benachbarte Vollkonjunktionen, Feldwerte 1, oder benachbarte Volldisjunktionen, Feldwerte 0, zusammenfassen. Hat man sich für Vollkonjunktionen (UND) entschieden, dann werden eingetragene 0-Werte nicht berücksichtigt. Eine entsprechende Regel gilt für Volldisjunktionen (ODER). KV-Diagramme mit zwei Eingangsvariablen sind sehr einfach zu überblicken. Die Skizze zeigt diese KV-Diagramme mit erlaubten Blöcken für Minterme.

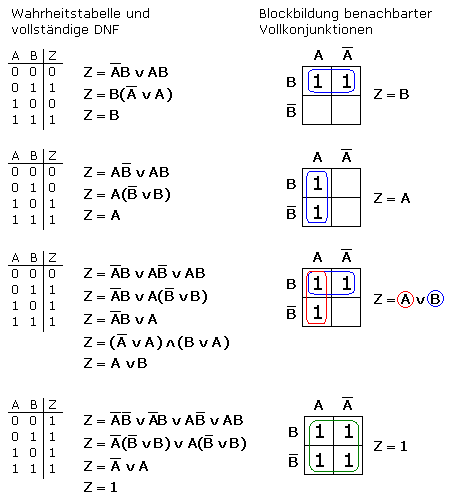
Optimierte DNF aus dem KV-Diagramm

• Es werden Blöcke mit Minterme, Feldwerte 1 gebildet.
• Alle im Block gemeinsam vorkommenden Variablen bilden durch UND verknüpft den Gleichungsterm.
• In der Funktionsgleichung sind alle Gleichungsterme disjunktiv durch ODER verknüpft.

Optimierte KNF aus dem KV-Diagramm

• Es werden Blöcke mit Maxterme, Feldwerte 0 gebildet.
• Alle Variablen, die im Block nicht vorkommen, bilden durch ODER verknüpft den Gleichungsterm.
• Alternativ können auch alle Variablen, die im Block vorkommen durch ODER verknüpft werden.
  Anschließend sind die Variablen dann noch zu negieren.
• In der Funktionsgleichung sind alle Gleichungsterme konjunktiv durch UND verknüpft.

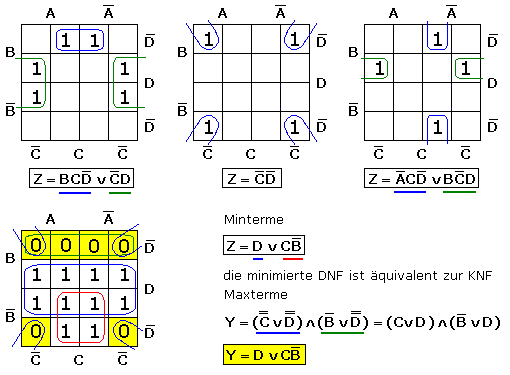
Die folgenden drei Beispiele zeigen für Minterme das Erstellen der Funktionsgleichung aus der Wahrheitstabelle mit vollständiger DNF die Optimierung durch die Schaltalgebra oder direkt aus dem KV-Diagramm. Die Blockbildung erfolgt mit benachbarten Vollkonjunktionen. Dabei sollten größtmögliche Schleifen gebildet und überflüssige Schleifen vermieden werden.

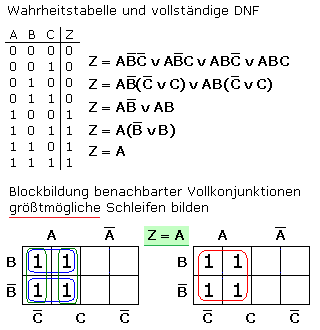
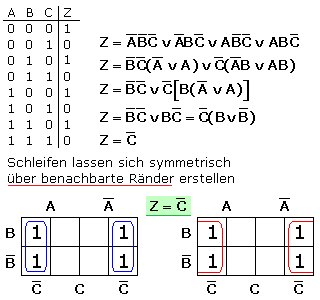
Das letzte Beispiel zeigt, dass auch mit den Maxtermen die Funktionsgleichung aus dem KV-Diagramm ausgelesen werden kann. Dazu werden Blöcke mit den Feldwerten 0 gebildet. Die dort gemeinsam auftretenden Variablen werden negiert durch ODER verknüpft und die Einzelterme dann durch UND verknüpft.

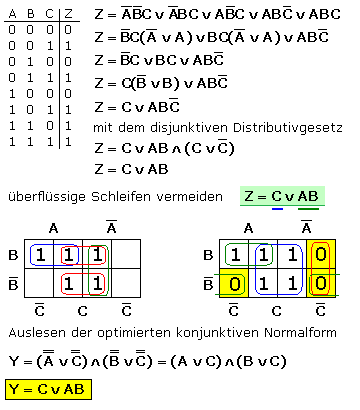
KV-Diagramme für vier Eingangsvariable bieten noch mehr Möglichkeiten zur Blockbildung. Das folgende Bild zeigt einige Beispiele zum Erstellen der Funktionsgleichung nach der DNF. Auch hier zeigt das letzte Beispiel, dass mit dem KV-Diagramm gleichermaßen auf Minterme oder Maxterme angewendet recht schnell die optimierte Funktionsgleichung ermittelt werden kann.