Die Spule im Gleichstromkreis

Wird ein langer Leiterdraht in aufeinanderfolgenden Windungen auf einen nichtleitenden mechanischen Träger ein- oder mehrlagig aufgewickelt, so entsteht eine Spule. Sie hat immer einen Widerstandswert, der bei Kenntnis der Drahtlänge, dem Drahtquerschnitt und der elektrischen Leitfähigkeit des Drahts errechnet werden kann. Zusätzlich zu diesem Wirkwiderstand hat jede Spule eine Induktivität.

Wird Gleichspannung an einen Wirkwiderstand gelegt, dann fließt sofort der nach dem Ohm'schen Gesetz errechnete maximale Strom. Bei einer Spule mit ihrem Drahtwiderstand und vielen Windungen nimmt der Strom nichtlinear zu und erreicht erst nach einer bestimmten Zeit den maximalen Strom, der dann vom Drahtwiderstand bestimmt ist. Dieses Verhalten kann sehr gut mit einem Zweikanal Oszilloskop dargestellt werden. Generell sind Oszilloskope Spannungsmessgeräte, daher muss für die Strommessung ein kleiner Widerstand in Reihe zur Spule geschaltet werden. Die Spannung an diesem Messwiderstand ist proportional zum Strom durch die Spule, der vom zweiten Kanal als Spannungsverlauf dargestellt wird.

In einem sich ändernden äußeren Magnetfeld (magnetische Fremderregung) erzeugt eine Spule an ihren Anschlüssen eine sich ändernde (Selbst)induktionsspannung. Fließt elektrischer Strom durch eine Spule, so entsteht senkrecht zur Stromrichtung um jede Leiterwindung ein magnetischer Fluss. Bei einer Stromänderung ändert sich proportional der magnetische Fluss und die Spule reagiert auf ihr sich änderndes Magnetfeld. Sie generiert eine (Selbst)induktionsspannung Uind und wird zur Spannungsquelle. Nach der Lenz'schen Regel muss Uind so gerichtet sein, dass sie der Stromänderung entgegen wirkt. Im Erzeugerzählpfeilsystem sind die Zählpfeilrichtungen für Spannung und Strompfeil entgegengesetzt.

Beide Messgrößen zeigen einen nichtlinearen exponentiellen Verlauf. Das Verhalten einer Spule im Gleichstromkreis ist prinzipiell vergleichbar mit dem Aufladen eines Kondensators an einer DC-Quelle. Im Unterschied zum Kondensator, wo nach dem Aufladen die Quellenspannung am Kondensator messbar ist und kein Strom fließt, ist an der Spule praktisch keine Spannung messbar, während der maximale Strom fließt. Der Kondensator speichert die aufgenommene Energie im elektrischen Feld. Die Spule speichert die zugeführte Energie in einem konstanten Magnetfeld und ist auf den dauerhaften Strom angewiesen.

Schaltdiagramme im Gleichstromkreis

Der folgende Videoclip zeigt für drei verschiedene Induktivitäten die Ein- und Ausschaltvorgänge. Der Drahtwiderstand der Spule ist im Vorwiderstand enthalten. Für den Einschaltprozess ist die Schaltung mit einer Konstantspannungsquelle verbunden. Beim Ausschaltprozess ist die DC-Quelle abgetrennt und der Vorwiderstand bildet mit der Spule den geschlossenen Stromkreis. Für jeden Versuchsabschnitt hat die Spule ihre vorgegebene konstante Induktivität während der Vorwiderstand für den Ein- und Ausschaltprozess einen anderen Widerstandswert hat. Der Videoclip kann nur mithilfe der einblendbaren Controlleiste gesteuert werden.

Wird der Stromkreis zur DC-Quelle geschlossen dann ist vom Zeitpunkt t = 0 ausgehend die zeitliche Stromänderung dI/dt anfangs am stärksten und erreicht mit abnehmender Änderungsrate den endgültigen Maximalstrom. Das scheint für eine Schaltung mit einem Drahtwiderstand ungewöhnlich zu sein. Jede reale Spule ist eine Reihenschaltung des konstanten Drahtwiderstands RCu mit der idealen Induktivität L (Spule). Die angelegte DC-Quellenspannung ist konstant, folglich muss die Spule mit ihrer Induktivität als Spannungsquelle wirken. Für die (Selbst)induktionsspannung gibt es in Formelsammlungen für lange Spulen eine Funktionsgleichung, die an dieser Stelle nicht hergeleitet wird. In dieser Funktion ist L die Induktivität der Spule mit der Einheit Henry \(1\,H = 1\,Vs/A\): \[{U_{ind}}(t) = L \cdot \frac{{dI}}{{dt}}\quad mit\quad L = {\mu _o}{\mu _r}{n^2}\frac{A}{l}\]

Die folgende Grafik zeigt, dass nach dem Einschalten der zeitliche Stromanstieg am stärksten zunimmt, also positiv ist. Die DC-Quelle wird von der Spule und ihrem in Reihe geschalteten konstanten Drahtwiderstand belastet. Im Zählpfeilsystem der Verbraucherschaltung weisen Spannungs- und Strompfeile in die gleiche Richtung. Nach der Funktionsgleichung ist die (Selbst)induktionsspannung positiv und anfangs sehr hoch.

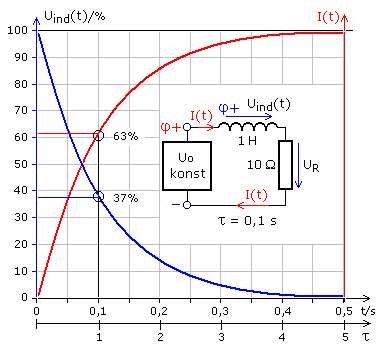
Es kann eine Maschengleichung aufgestellt werden: \({U_o} = {U_{ind}}(t) + {U_R}(t)\). Die Spannungen an den beiden Lastwiderständen wird vom zeitlich abhängigen Strom I(t) bestimmt, der nach einiger Zeit den konstanten Maximalstrom Io erreicht. Dieser errechnet sich nach dem Ohm'schen Gesetz aus der Quellenspannung und dem Widerstandswert. Für die Stromänderung gilt die Exponentialfunktion: \[I(t) = {I_o} \cdot (1 - {e^{ - t/\tau }})\;\;\,\quad (1)\] Ist der Stromkreis geschlossen, so fließt zum Zeitpunkt t = 0 kein Strom und die Spannung am Widerstand ist null. Das bedeutet, dass sich die Spule wie eine Spannungsquelle verhält und die Induktionsspannung Uind(t) gleich der Quellenspannung Uo sein muss. Sie hat ihr positives Potenzial (φ+ blau) dort, wo sie mit dem Pluspol der DC-Quelle verbunden ist. Im Einschaltmoment ist das Potenzial der DC-Quelle (φ+ rot) gleich dem Spulenpotenzial (φ+ blau) und die Potenzialdifferenz, also die Spannung, die den Strom im Stromkreis verursacht, ist null. Die Lenz'schen Regel ist erfüllt, da die Spule mit ihrem Verhalten der von der DC-Quelle ausgehenden Stromänderung entgegen wirkt.

Nach einer bestimmten Zeit ändert sich der Strom nicht mehr und ist mit I(t) = Io konstant. Diese Zeit ist das Fünffache der Zeitkonstanten \(\tau = L/R\). Die (Selbst)induktionsspannung der Spule muss dann null sein und der Maximalstrom Io wird vom Wirkwiderstand in der Schaltung bestimmt. Solange Io fließt, speichert die Spule Energie im dann konstanten Magnetfeld.

Mathematische Herleitung des Einschaltvorgangs

Für die reale Spule an einer konstanten DC-Quellenspannung gilt für die RL-Reihenschaltung die weiter oben aufgestellte Maschengleichung. Aus dem Videoclip und Laborversuchen sind zwei Randbedingungen bekannt. Zum Zeitpunkt des Einschaltens fließt bei t = 0 kein Strom und nach einiger Zeit fließt der vom Wirkwiderstand begrenzte Maximalstrom. Für die Zeitabhängigkeit des Stroms kann die folgende Gleichung aufgestellt werden: \[\begin{array}{l} U(t) = {U_o} + {U_{ind}}(t)\quad \quad {U_{ind}}(t) = - L\frac{{d\,I(t)}}{{dt}}\\ U(t) = R\,I(t) = {U_o} - L\frac{{d\,I(t)}}{{dt}} \end{array}\] Es wird durch L dividiert und nach dem Umstellen ist als Ergebnis eine inhomogene Differenzialgleichung (DGL) zu erkennen: \[\frac{R}{L}\,I(t) = \frac{{{U_o}}}{L} - \frac{{d\,I(t)}}{{dt}}\quad \Rightarrow \quad \frac{{d\,I(t)}}{{dt}} + \frac{R}{L}\,I(t) = \frac{{{U_o}}}{L}\quad (2)\] Für sie kann ein Lösungsansatz mit einer Exponentialfunktion (e-Funktion) vermutet werden. Um die Endbedingung für den Maximalstrom zu erfüllen muss der Exponent negativ sein: \[I(t) = {I_o} - {I_o} \cdot {e^{ - k\,t}} = {I_o}\,(1 - {e^{ - k\,t}})\] Sie erfüllt die beiden Randbedingungen. Zum Zeitpunkt t = 0 ist das Ergebnis I(t) = 0. Zum Zeitpunkt t → ∞ ist wegen des negativen Exponenten I(t) = I0. Dieser Lösungsansatz wird mit der Kettenregel abgeleitet und in die vorherige Funktion Gl.(2) eingesetzt und schrittweise umgeformt: \[\begin{array}{l} \frac{{dI(t)}}{{dt}} = {I_o} \cdot k \cdot {e^{ - k\,t}}\\ {I_o} \cdot k \cdot {e^{ - k\,t}} + \frac{R}{L}\,I(t) = \frac{{{U_o}}}{L}\quad \quad {U_o} = R\,{I_o}\\ {I_o} \cdot k \cdot {e^{ - k\,t}} + \frac{R}{L}\left( {{I_o} - {I_o} \cdot {e^{ - k\,t}}} \right) = \frac{{R\,{I_o}}}{L}\\ {I_o} \cdot k \cdot {e^{ - k\,t}} + \frac{{R\,{I_o}}}{L} - \frac{R}{L}{I_o} \cdot {e^{ - k\,t}} = \frac{{R\,{I_o}}}{L}\\ {I_o} \cdot {e^{ - k\,t}}\left( {k - \frac{R}{L}} \right) = 0\quad \Rightarrow \quad k = \frac{R}{L} \end{array}\]

Die angenommene e-Funktion erfüllt den im Videoclip und im Labor messbaren Stromverlauf. Der Kehrwert von k ist die oben im Diagramm eingetragene Teilung der Horizontalachse mit der Zeitkonstanten \(\tau = L/R\). Der Widerstand R ist der Summenwiderstand der Reihenschaltung aus dem Drahtwiderstand der Spule, dem Innenwiderstand der DC-Quelle und einem weiteren vielleicht vorhandenen konstanten Vorwiderstand.

Ändert sich der magnetische Fluss, der eine Spule durchdringt, so generiert sie eine Induktionsspannung. Der magnetische Fluss ist proportional zur Stromänderung. Nach der Lenz'schen Regel muss die Induktionsspannung so gerichtet sein, dass sie der Stromänderung entgegen wirkt. Die Änderung der Induktionsspannung kann wie folgt bestimmt werden: \[\begin{array}{l} {U_{ind}}(t) = - N\frac{{d\Phi }}{{dt}}\quad \quad d\Phi \propto d{I_L}\\ {U_{ind}}(t) = - L\frac{{d{I_L}}}{{dt}}\quad in\;\frac{{Vs}}{A} \cdot \frac{A}{s} = V\\ \frac{{dI}}{{dt}} = \frac{{{U_o}}}{L} \cdot {e^{ - t/\tau }}\\ {U_{ind}}(t) = - {U_o} \cdot {e^{ - t/\tau }} \end{array}\] Die Induktionsspannung ist der anliegenden Quellenspannung entgegengerichtet. Sie hat im Einschaltmoment den Wert der Quellenspannung und beim aufgebauten statischen Magnetfeld den Wert null: \[t = 0\quad \Rightarrow {U_{ind}}(0) = - {U_o}\quad und\quad t \to \infty \quad \Rightarrow {U_{ind}}(\infty ) = 0\] In beiden hergeleiteten e-Funktionen steht im Exponent die Zeitkonstante \(\tau = L/R\). Für den Einschaltvorgang gelten die folgenden Formeln:

Spannungsverlauf am Vorwiderstand

\({U_R}(t) = {U_o}\left( {1 - {e^{ - t/\tau }}} \right)\)

Spannungsverlauf an der Spule

\({U_L}(t) = - {U_o} \cdot {e^{ - t/\tau }}\)

Stromverlauf

\(I(t) = \frac{{{U_o}}}{R}\left( {1 - {e^{ - t/\tau }}} \right)\)

Abschaltprozess

Hat sich das Magnetfeld vollständig aufgebaut und die DC-Quelle wird abgeschaltet oder aus dem Stromkreis entfernt, so bleibt das Magnetfeld nicht erhalten. Das ist bei einem auf die Endspannung aufgeladenen Kondensator anders, denn er behält die Ladung und damit die Spannung über lange Zeit. Im Videoclip wird nach dem Aufbau des Magnetfelds der Vorwiderstand von der DC-Quelle getrennt und zur Schaltungsmasse umgeschaltet. Die Messungen zeigen, dass der Strom in die gleiche Richtung wie vorher fließt. Das setzt voraus, dass beim Umschalten die Spule eine hohe Spannung generiert, deren Vorzeichen entgegengesetzt wie zum Einschaltvorgang gepolt ist. Die Spannungshöhe entspricht der vorherigen Quellenspannung da im Umschaltmoment gerade noch der Maximalstrom als Entladestrom fließt. Das Magnetfeld baut sich ab und die nach dem Induktionsgesetz generierte Spannung verringert ebenso wie der Strom. Nach fünf Zeitkonstanten haben alle Größen ihren Endwert null erreicht.

Mathematische Herleitungen

Der Strom nimmt nach einer e-Funktion ab. Die zeitliche Stromänderung wird mithilfe der 1. Ableitung dieser Funktion bestimmt: \[I(t) = \frac{{{U_o}}}{R} \cdot {e^{ - t/\tau }} = {I_o} \cdot {e^{ - t/\tau }}\quad \quad \tau = \frac{L}{R}\quad \quad R = {R_{Cu}} + {R_v}\] \[\frac{{dI(t)}}{{dt}} = {I_o} \cdot \left( { - \frac{1}{\tau }} \right) \cdot {e^{ - t/\tau }} = - \frac{R}{L} \cdot {I_o} \cdot {e^{ - t/\tau }}\quad \] Die Grenzwertbetrachtung zeigt, dass zur Umschaltzeit t = 0 der Maximalstrom fließt und nach ausreichend langer Zeit (5 Zeitkonstanten) der Strom gegen null geht. Wie schnell der Strom abnimmt wird bei derselben Induktivität vom Entladewiderstand bestimmt. In der e-Funktion steht im Exponenten der Widerstand R im Zähler. Je größer der Wert ist, desto steiler verläuft die e-Funktion und der Strom nimmt schneller ab.

Die Änderung der Induktionsspannung kann mit dem gleichen Ansatz hergeleitet werden, der weiter oben für den Einschaltmoment angewendet wurde. \[\begin{array}{l} {U_{ind}}(t) = - L \cdot \frac{{dI(t)}}{{dt}} = - L\left[ { - \frac{R}{L} \cdot {I_o} \cdot {e^{ - t/\tau }}} \right]\\ {U_{ind}}(t) = R \cdot {I_o} \cdot {e^{ - t/\tau }} \end{array}\] Sind zur Startzeit t = 0 des Abschaltvorgangs die Spule und der Widerstand gleich geblieben, dann erzeugt die Spule eine Induktionsspannung die gleich der vorher angelegten Quellenspannung \(R \cdot {I_o} = {U_o}\) ist. Die Änderungsrate der Induktionsspannung wird mit der 1. Ableitung bestimmt: \[\frac{{d{U_{ind}}(t)}}{{dt}} = {U_o} \cdot \left( { - \frac{1}{\tau }} \right) \cdot {e^{ - t/\tau }} = - \frac{R}{L}{U_o} \cdot \left( { - \frac{1}{\tau }} \right) \cdot {e^{ - t/\tau }}\] Die Grenzbetrachtung zeigt, dass bei t = 0 die Induktionsspannung ihren Maximalwert hat und dann abnimmt, um nach 5 Zeitkonstanten praktisch den Wert null erreicht hat. Für den Ausschaltvorgang gelten für den Strom- und Spannungsverlauf die folgenden allgemeinen Gleichungen:

Stromverlauf

\(I(t) = \frac{U}{R} \cdot {e^{ - t/\tau }} = I \cdot {e^{ - t/\tau }}\)

Spannungsverlauf am Widerstand

\({U_R}(t) = U \cdot {e^{ - t/\tau }}\)

Spannungsverlauf an der Spule

\({U_L}(t) = - U \cdot {e^{ - t/\tau }}\)

Schutzvorkehrung gegen hohe Induktionsspannungen beim Abschalten

Mit einem Simulationsprogramm kann die Abschaltspannung gemessen werden. Eine Spule mit 100 mH und 10 Ω Drahtwiderstand wurde an U = 1 V Gleichspannung angeschlossen. Nach dem Erreichen des maximalen Gleichstroms I = 100 mA wurde die Spule von der DC-Quelle zum Entladewiderstand R = 90 Ω nach Masse umgeschaltet. Zum Zeitpunkt der Unterbrechung errechnet sich die Induktionsspannung an der Spule zu 10 V. Die Simulation bestätigt das Ergebnis. Die Zeitkonstante zur Abschaltphase beträgt τ = 1 ms.

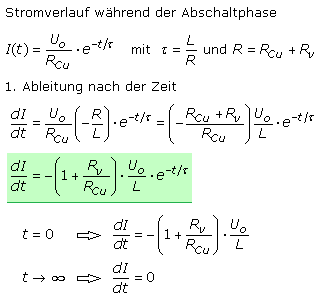
Bei gleicher 1 V Betriebsspannung aber einem Entladewiderstand von 990 Ω erreicht die Spannungsspitze im Abschaltmoment den Wert 100 V. Laststromkreise werden oft mit Relais geschaltet, deren transistorisierte Steuerschaltung mit Niederspannung von 12 bis 24 Volt und einem Arbeitsstrom von 50 mA erfolgt. Wird das Relais abgeschaltet, dann ist der Transistor extrem hochohmig. Die Spannungsspitze der Spule kann Werte erreichen, die oberhalb der erlaubten Kollektor-Emitter-Sperrspannung liegen. Zum Schutz des Transistors wird parallel zur Relaisspule eine sogenannte Freilaufdiode geschaltet. Zur DC-Betriebsspannung der Transistorschaltung ist sie in Sperrrichtung geschaltet. Im Abschaltmoment wird die Diode leitend und begrenzt den Spitzenwert der Induktionsspannung der Spule auf die Dioden Durchlassspannung <1 V.

Werden größere Induktivitäten mit mechanischen Schaltern geschaltet, dann entspricht der Abschaltwiderstand dem Isolationswiderstand zwischen den Kontakten. Trockene Luft beim Normaldruck von 1 bar ≈ 1013,25 hPa und 20°C isoliert rund 3 kV pro Millimeter. Ohne Schutzmaßnahmen bilden sich Funkenstrecken mit Kontaktabbrand oder die Kontaktflächen verschweißen miteinander. Mit einem parallel geschalteten Widerstand oder einer RC-Reihenkombination können die Schaltkontakte im AC-Betrieb geschützt werden. Im DC-Betrieb ist eine antiparallel geschaltete Freilaufdiode gut geeignet.

Reihenschaltung von Spulen

Sind in einem Stromkreis mehrere Induktivitäten in Reihe geschaltet und beeinflussen sich ihre Magnetfelder gegenseitig nicht, dann ist die Gesamtinduktivität gleich der Summe der Einzelwerte. \({L_{ges}} = {L_1} + {L_2} + \cdots + {L_n}\)

Parallelschaltung von Spulen

Für parallel geschaltete Spulen, deren Magnetfelder sich gegenseitig nicht beeinflussen, berechnet sich die Gesamtinduktivität für mehrere und für 2 Spulen wie folgt: \[{L_{ges}} = \frac{1}{{\frac{1}{{{L_1}}} + \frac{1}{{{L_2}}} + \cdots + \frac{1}{{{L_n}}}}}\quad \quad {L_{ges}} = \frac{{{L_1} \cdot {L_2}}}{{{L_1} + {L_2}}}\]

Magnetische Energie einer Spule

Eine an Gleichspannung angeschlossene reale Spule erhält elektrische Energie. Ein Teil wird am Wirkwiderstand in Wärme umgesetzt. Der größere Teil wird im Magnetfeld gespeichert. Da es sich um einen nichtlinearen dynamischen Vorgang handelt, kann nur mit differenziell kleinen Zeitabschnitten gerechnet werden. Die endgültige Beziehung ergibt sich durch Integration. \[\begin{array}{l} u = {u_R} + {u_L}\\ d{W_{el}} = d{W_{therm}} + d{W_{magn}}\\ d{W_{magn}} = {u_L} \cdot {i_L}\,dt\quad mit\quad {u_L} = L\frac{{di}}{{dt}}\\ d{W_{magn}} = L\frac{{di}}{{dt}} \cdot {i_L}\,dt = L \cdot {i_L}\,di\\ {W_{magn}} = L\int\limits_0^I {{i_L}\,di} \\ {W_{magn}} = \frac{1}{2}L \cdot {I^2}\quad \frac{{V\,s}}{A}{A^2} = W\,s \end{array}\]

Weitere Informationen zur Spule im Wechselstromkreis sind auf der Seite: Wechselstromwiderstände, induktiver Blindwiderstand zu finden.