Elektrische Leitungen
Im Stromkreis sind elektrische Geräte und Baugruppen durch elektrische Leitungen, Kabel oder Einzeldrähte miteinander verbunden. Umgangssprachlich führt alles zum Ziel, es gibt differenziertere Beschreibung in Anlehnung an das Lexikon der Nachrichtentechnik der SEL – Standard Elektric Lorenz AG. Auf dieser Seite gibt es einfach gehaltene Erklärungen zur allgemeinen Leitungstheorie, wo der Leitungswellenwiderstand theoretisch und experimentell behandelt wird. Zur Theorie passend sind die Ergebnisse einiger Labor- und Simulationsergebnisse. Bestimmt wurde die Signalgeschwindigkeit und Wellenlänge und Reflexionen für die angepasste und nicht angepasste Leitung. Im letzten Teil wird der bei hohen Frequenzen zunehmende Einfluss des Skin-Effekts beschrieben und für wenige Beispiele berechnet.
- Draht
- Draht ist ein metallisches Erzeugnis von geringem, meist rundem Querschnitt und großer Länge. Durchmesser bis 5 mm werden durch Walzverfahren hergestellt. Geringere Durchmesser bis 0,01 mm entstehen im wiederholten Ziehverfahren durch Zieheisen oder Ziehsteine. Wird Platindraht mit Silber ummantelt, so lassen sich im Ziehverfahren nach Wegätzen des Silbers Platindrahtdurchmesser von einigen μm herstellen (nach Duden Lexikon).
- Leiter
- In der Verbindungstechnik fließt der elektrische Strom durch einen metallischen Leiter. Der Leiterdurchmesser wird in Millimetern angegeben und ohne die Isolierung gemessen.
- Leitung
- Als technischer Begriff ist es eine durch Schaltanweisungen in technischen Merkmalen und Schaltpunkten vorgegebene Hintereinanderschaltung von Versorgungsstromkreisen. In bestimmten Einrichtungen wird die Leitung zur Übertragung elektrischer Signale benutzt.
- Leitungsbündel
- Die Summe aller Leitungen zwischen zwei Endpunkten wird als Leitungsbündel bezeichnet.
- Kabel
- Das Kabel fasst mehrere isolierte Leiter unter einer gemeinsamen Schutzhülle zusammen und dient der Fortleitung elektrischer Energie oder Nachrichtensignale.
- Ader, Adernpaar, Doppelader
- Der Leiter mit seiner Isolierhülle wird als Ader bezeichnet. Bei Innenkabeln bilden zwei miteinander verseilte Adern einen Leitungskreis. Ein symmetrisches Adernpaar ist die Anordnung zweier Leiter mit gleichem Durchmesser und gleichartiger Isolierung, die zueinander eine räumlich definierte Lage haben. Die Doppelader bei Kabeln ist das aus zwei Adern eines Paares bestehende Übertragungselement.
- Koaxialpaar (KxP)
- Das Koaxialpaar ist ein Leiterpaar mit einem konzentrisch um den Innenleiter angeordneten Außenleiter. Beide Leiter sind gegeneinander durch Isoliermaterial, dem Dielektrikum im festen Abstand abgestützt. Diese Anordnung wird auch Koaxialtube (englisch Tube) genannt.
- Koaxialkabel (KxK)
- Es handelt sich um einzelne Koaxialkabel. Für große Anlagen können mehrere Koaxialkabel zusammengeschlossen sein, um Analogübertragungen breiter Frequenzbänder (TF-Tonfrequenz oder TV-Fernseh-Video-Signale) oder Übertragungen von Digitalsignalen mit hohen Übertragungsraten zu ermöglichen. Beim Koaxialkabel sind die ohmschen Widerstände vom Innen- und Außenleiter sind fast immer unterschiedlich. Die Werte werden sind im Datenblatt getrennt und zum Teil durch den ohmschen Schleifenwiderstand ergänzt angegeben.
- Twisted Pair
- Darunter werden paarweise verdrillte Zweidrahtleitungen verstanden. Mit einer zusätzlichen äußeren Schirmung können elektrische Störeinflüsse auf das Twisted Pair gedämpft werden.
Allgemeine Leitungstheorie
Zur Übertragung von Gleichstrom und sehr niederfrequentem Wechselstrom über nicht zu lange Strecken ist praktisch nur der ohmsche Leiterwiderstand von Interesse. Bei der Signalübertragung hoher Frequenzen müssen weitere Leitungseigenschaften berücksichtigt werden. Die Signale eines breiteren Frequenzbandes sollen die Leitung möglichst unverfälscht passieren. Die Signalübertragung erfolgt im einfachsten Fall durch eine auf das Signal bezogene symmetrische Leitung oder eine unsymmetrische Koaxialleitung. Eine symmetrische Leitung mit einem Adernpaar ist meistens eine einfache Zweidrahtleitung. Sie kann auch mit besonderen geometrischen Eigenschaften ausgerüstet werden. Eine Stegleitung hat zwei gleiche Einzeladern eingebettet in ein flaches Isolationsmaterial definierter Breite. Beim Twisted Pair sind zwei gleiche Einzeladern mit konstantem Drehsinn verdrillt.
Jeder Draht hat einen ohmschen Widerstand. Im Zeigerdiagramm wird er in Richtung der horizontalen Realwertachse (Re-Achse) gezeichnet. Würde der Draht zu einer Spule gewickelt werden, so hat diese einen induktiven Blindwiderstand. Er ist von der Frequenz abhängig und im Zeigerdiagramm wird er in Richtung der vertikalen Imaginärwertachse (Im-Achse) gezeichnet. Da ein Leiterdraht vergleichbar mit einem abgewickelten Spulendraht ist, hat er mit der Windungszahl n = 1 eine kleinere Induktivität. Ein Stromkreis besteht aus einem Hin- und Rückleiter. Parallel laufende Hin- und Rückleiter sind vergleichbar mit einem Plattenkondensator. Eine Doppelleitung hat somit geringe kapazitive Eigenschaft und einen von der Frequenz abhängigen kapazitiven Blindwiderstand. Die folgenden Beschreibungen gelten für längshomogene Leitungen zur Übertragung von DC und sinusförmigen periodischen AC-Signalen.
Für elektrische Signale ist jede Leitung durch ein passives Zweitor (Vierpol) beschreibbar. Bei einer (längs)homogenen Leitung verteilen sich die genannten Eigenschaften wie Widerstand, Induktivität und Kapazität gleichmäßig entlang der gesamten Leitung. Ein- und Ausgang einer Leitung können getauscht werden. Die Leitung entspricht in ihren Eigenschaften einem symmetrischen Vierpol wird aber vereinfacht mit idealer Rückleitung dargestellt. Die zur Leitungslänge proportionalen Widerstands-, Induktivitäts- und Kapazitätswerte werden als Belagswerte R', L' und C' bezeichnet. Sie sind auf eine Längeneinheit in m oder km bezogen. Haben beide Leiter eine identische Isolierung und bestehen aus dem gleichen Material, so besteht auch eine Querhomogenität. Der Isolationswert wird als paralleler ohmscher Querleitbelag G' in der Einheit Siemens pro Längeneinheit angegeben. Die folgende Darstellung zeigt Schaltbilder verlustbehafteter längshomogener Leitungselemente der infinitesimalen Länge dx. Der Leitungswiderstand wird von allen Leitungsparametern R', L', C' und G' bestimmt. Er ist von der Frequenz abhängig und wird als Leitungswellenwiderstand oder Impedanz bezeichnet. Die Einheit der Impedanz ist Ohm. Es ist eine komplexe Größe und kann am Bauteil Leitung nicht direkt wie beim ohmschen Widerstand gemessen werden.
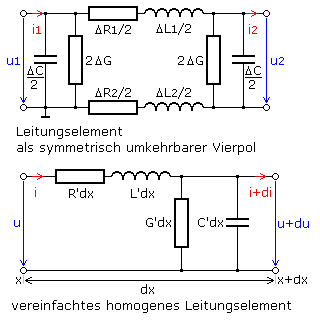
Das Ersatzschaltbild zeigt, dass jede elektrische Leitung Tiefpasscharakter hat.
Der Widerstandsbelag R'
In Datenblättern können Angaben zum Schleifenwiderstand eines Adernpaars und/oder Einzelwiderstandswerte der Hin- und Rückleitung zu finden sein. Die Einheit für R' ist Ω/m oder Ω/km. Mit zunehmender Frequenz nimmt der ohmsche Wechselstromwiderstand der Leitung zu, da durch den Skin-Effekt der Stromtransport zur Leiteroberfläche hin verdrängt wird. Der Leiterkern wird mehr und mehr stromfrei und der noch aktiv vom Strom durchflossene Leiterquerschnitt kleiner. Das entspricht einem größeren Widerstandswert. Für dünne Leitungsdrähte und Signalfrequenzen unterhalb 1 MHz wird der Skin-Effekt praktisch nicht berücksichtig. Der Schleifenwiderstand kann durch eine Spannungs- und Strommessung der am Ende kurzgeschlossenen Leitung messtechnisch ermittelt werden. Dieser ohmsche Wirkwiderstand dividiert durch die Leitungslänge in Ω/m entspricht dem Widerstandsbelag R' der Doppelleitung.
Der Induktivitätsbelag L'
Der Wert setzt sich aus einem äußeren und inneren Induktivitätsbelag zusammen. Der äußere Induktivitätsbelag ist vom geometrischen Leitungsaufbau und von den magnetischen Eigenschaften des Leiters abhängig. Normalerweise werden keine ferromagnetischen Leiter verwendet, somit kann für die magnetische Permeabilität \({\mu _r} = 1\) gesetzt werden. Der viel kleinere innere Induktivitätsbelag beruht auf magnetischen Wechselfeldern innerhalb des Leiters. Er ist verantwortlich für den Skin-Effekt, wo mit zunehmender Frequenz die Stromdichte zur Leiteroberfläche verdrängt wird. Die folgenden Betrachtungen gelten für Leitungen mit geringem Querschnitt, deren induktive Eigenschaft für Signalfrequenzen oberhalb 50 kHz überwiegend von der äußere Induktivität bestimmt wird. Die Einheit des Induktivitätsbelags L' ist H/m.
In guten Formelsammlungen gibt es Formeln zur Berechnung der Induktivität langer Doppelleitungen und Koaxialleitungen. Bei symmetrischen Doppelleitungen müssen der Leiterradius r oder Durchmesser 2·r sowie der Mittelpunktsabstand a zwischen den beiden Adern bekannt sein. Der längenbezogene Wert ist dann Induktivitätsbelag L'. Ist der Quotient a/2r ≥ 10 so gilt die folgende Herleitung: \[\begin{array}{l} L' = \frac{{{\mu _o}}}{\pi }ar\cosh \left( {\frac{a}{d}} \right) = \frac{{{\mu _o}}}{\pi }ar\cosh \left( {\frac{a}{{2\,r}}} \right)\\ L' = \frac{{{\mu _o}}}{\pi }\ln \left( {\frac{a}{{2\,r}} + \sqrt {{{\left( {\frac{a}{{2\,r}}} \right)}^2} - 1} } \right)\\ L' = \frac{{{\mu _o}}}{\pi }\ln \left( {2\frac{a}{{2\,r}}} \right) = \frac{{{\mu _o}}}{\pi }\ln \left( {\frac{a}{r}} \right) \end{array}\] Zur Berechnung des Induktivitätsbelags einer Koaxialleitung muss der Radius oder Durchmesser des Innenleiters und der innere Durchmesser des Außenleiters (Schirmung) bekannt sein. Ist der Radius des Innenleiters mit \({r_i} \ll {r_a}\) dann kann der Induktivitätsbelag in guter Näherung mit der folgenden Gleichung berechnet werden: \[L{'_{koax}} \approx L{'_{aussen}} = \frac{{{\mu _o}}}{{2\,\pi }}\ln \frac{{{r_a}}}{{{r_i}}}\quad \quad {\mu _o} \approx 4 \cdot \pi \cdot {10^{ - 7}}\;\frac{H}{m}\]
Der Kapazitätsbelag C'
Die Kapazität C ist abhängig vom geometrischen Aufbau der Leitung und vom Dielektrizitätswert \({\varepsilon _r}\), der nunmehr als Permittivität oder dielektrische Leitfähigkeit bezeichnet wird. Der Kapazitätsbelag C' ist ein längenbezogener Wert mit der Einheit F/m. Das Vakuum hat mit der elektrischen Feldkonstante \({\varepsilon _o}\) ebenfalls eine Permittivität. Es ist die Naturkonstante mit dem Wert: \[{\varepsilon _o} = \frac{1}{{{\mu _o}c_o^2}} = 8,8541878128 \cdot {10^{ - 12}}\;\frac{{A\,s}}{{V\,m}}\] Die Permittivität ist das Produkt \(\varepsilon = {\varepsilon _o} \cdot {\varepsilon _r}\). Für Luft kann in guter Näherung \({\varepsilon _r} = 1\) gesetzt werden.
In Formelsammlungen gibt es zur Berechnung der Kapazität C langer Leitungen verschiedene Formeln. Zur Berechnung der Kapazität einer symmetrischen Paralleldrahtleitungen, die als Überland-Freileitung auf Traversen installiert ist, muss der Drahtdurchmesser d oder der Radius r und der konstante Mittelpunktsabstand a beider Drähte bekannt sein. Die Leitungslänge l sollte groß zum Drahtabstand und dieser groß zum Drahtdurchmesser sein. \[C = \frac{{{\varepsilon _o}\,\pi \,l}}{{ar\cosh \left( {\frac{a}{d}} \right)}} = \frac{{{\varepsilon _o}\,\pi \,l}}{{\ln \left( {\frac{a}{d} + \sqrt {{{\left( {\frac{a}{d}} \right)}^2} - 1} } \right)}}\] Ist der Quotient a/d ≥ 10 so vereinfacht sich die Gleichung zu: \[C = \frac{{{\varepsilon _o}\,\pi \,l}}{{\ln \left( {2 \cdot \frac{a}{d}} \right)}} = \frac{{{\varepsilon _o}\,\pi \,l}}{{\ln \left( {2 \cdot \frac{a}{{2\,r}}} \right)}} = \frac{{{\varepsilon _o}\,\pi \,l}}{{\ln \left( {\frac{a}{r}} \right)}}\]
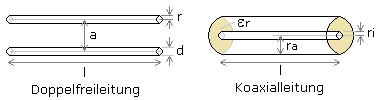
Für eine unsymmetrische Koaxialleitung müssen vom Mittelpunkt der Leitung der Innenradius des Leiterdrahts, der Außenradius zur Schirmung und die Leiterlänge gegeben sein. Ist es keine besonders dämpfungsarme Leitung so ist die Kapazität um den Faktor der Permittivität der durchgehenden inneren Isolierung größer: \[C = \frac{{2\,{\varepsilon _o}\,{\varepsilon _r}\,\pi \,l}}{{\ln ({r_a}/{r_i})}}\]
Der Ableitungsbelag G'
Der Wert G' mit dem Schaltzeichen eines ohmschen Widerstands hat die Dimension S/m. Der Wert des Isolationswiderstands ist sehr hoch. Der Signalstrom durch die Leitung wird praktisch nur vom ohmschen Leitungswiderstand beeinflusst. Als Parallelwiderstand zum Kondensator kennzeichnet er die Eigenschaften des Dielektrikums und damit die Isolation zwischen Hin- und Rückleiter. Im Bereich sehr hoher Frequenzen ist der Isolationswiderstand von der Frequenz abhängig. Anstelle von G' wird manchmal auch der Verlustfaktor tan δ genannt. Sein Wert errechnet sich zu \(\tan \delta = G'/(\,\omega \cdot C'\,)\).
Der Dämpfungsbelag α
Der Dämpfungsbelag mit dem Buchstaben Alpha (α) und ist von der Frequenz und vom Isolationsmaterial abhängig. Er kann bei einer beidseitig angepassten Leitung aus dem Dämpfungsmaß a bezogen auf die Leiterlänge l messtechnisch bestimmt werden. Der Dämpfungsbelag wird in Neper/km oder dB/100 m angegeben. Zwischen Neper und Dezibel gibt es die auf drei Nachkommastellen gerundete Umrechnungsgleichung: 1 Np = 8,686 dB. Für die Dämpfung a in dB gilt: \[a = 20 \cdot \lg ({U_e}/{U_a})\]
Mit dem Leitungswellenwiderstand Z (Leitungsimpedanz) berechnet sich der Dämpfungsbelag \(\alpha \) zu: \[\alpha = \frac{{R'}}{{2{\mkern 1mu} \,Z}} + \frac{{G'\,Z}}{2}\] Bei einer verlustlosen Leitung werden R' und G' als vernachlässigbar klein im Vergleich zu C' und L' gesetzt. Die hier nicht hergeleitete Formel zum Leitungswellenwiderstand vereinfacht sich mit R' = 0 und G' = 0 zu: \[Z = \sqrt {\frac{{R' + j\omega L'}}{{G' + j\omega C'}}} \approx \sqrt {\frac{{L'}}{{C'}}} \] Im Quotienten kürzen sich die imaginäre Einheit j und \(\omega = 2\,\pi \,f\) der Wellenwiderstand Z der verlustlose Leitung wird reell. Dieser Idealfall gilt nicht generell. Im Bereich niedriger Frequenzen ist R' im Vergleich zu L' noch nicht vernachlässigbar. Im Bereich sehr hoher Frequenzen treten zunehmend Ableitströme im Dielektrikum der Isolierung auf. Kondensatoren im Wechselstrombetrieb werden bei höheren Frequenzen merklich warm, es wird also Wirkleistung umgesetzt.
Leitungen und wichtige Betriebsfälle
Die Leitungstheorie ist sehr umfangreich und erfordert zum vollständigen Verständnis gute Kenntnisse der höheren Mathematik angefangen von komplexer Wechselstromrechnung bis hin zu Differenzialgleichungen und den von Maxwell aufgestellten Formel für elektrische und magnetische Felder. Das sind hier nicht Themen der folgenden Abschnitte. Wichtig sind die Belagswerte einer Leitung und die Feststellung, dass sie eine nicht direkt messbare Leitungsimpedanz besitzt. Eine Leitung kann auf unterschiedliche Weise betrieben werden. Immer ist der Leitungseingang mit einer Signalquelle verbunden.
- Angepasste Leitung
- Der Leitungsausgang wird mit dem ohmschen Widerstand belastet, der den Wert der Leitungsimpedanz hat. Es handelt sich um eine Impedanz angepasste Leitung, die das Eingangssignal an den Ausgang leitet, wo es vollständig umgesetzt wird. Auf der Leitung gibt es keine Signalreflexionen.
- Offene Leitung
- Der Ausgang der Leitung bleibt offen, die Leitung befindet sich im Leerlauf. Das ankommende Signal wird vollständig reflektiert und läuft zum Eingang zurück. Da der Ausgangswiderstand gleichsam unendlich groß ist wird die Signalspannung unverändert, also mit gleicher Phasenlage und der Signalstrom gespiegelt reflektiert. Auf der Leitung überlagert sich die hinlaufende mit der rücklaufenden Welle und es entsteht eine sogenannte Stehwelle.
- Kurzgeschlossene Leitung
- Der Kurzschluss am Leitungsausgang entspricht einem Widerstand mit null Ohm. Das dort eintreffende Signal wird vollständig zum Eingang reflektiert. Jetzt hat die Stromwelle die gleiche Phasenlage wie die ankommende Welle und die Spannungswelle ist dazu gespiegelt. Durch die Überlagerung zwischen Hin- und Rückwelle entsteht entlang der Leitung ebenfalls eine Stehwelle.
- Freileitungstyp
- Die Eigenschaften beim Freileitungstyp sind vergleichbar mit denen einer verlustlosen Leitung. Es besteht eine geringe von der Frequenz unabhängige Signaldämpfung. Für diesen Leitungstyp soll \(j\omega L' \gg R'\) und \(j\omega C' \gg G'\) sein. Der Leitungswellenwiderstand verhält sich praktisch reell. Bei längeren Koaxialkabeln mit einem im Inneren durchgehenden Dielektrikum ist die Dämpfung von der Frequenz abhängig und nimmt mit zunehmender Signalfrequenz deutlich zu. Nähere Angaben können in den Datenblättern der Hersteller gefunden werden.
- Kabeltyp
- Für diese Leitungen soll \(j\omega L' \ll R'\) und \(j\omega C' \gg G'\) gelten. Der Leitungswellenwiderstand ist eine komplexe Größe. Hat das Eingangssignal ein breiteres Frequenzspektrum wie im Sprachband analoger Telefonie, so gelangen Signalanteile unterschiedlicher Frequenzen mit verschiedenen Laufzeiten am Ausgang ein. Bei größeren Leitungslängen treten Laufzeitverzerrungen und von der Frequenz abhängig hohe Dämpfungen auf.
Der Leitungswellenwiderstand oder Leitungsimpedanz
Viele Leitungseigenschaften geben Hersteller in Datenblättern an. Sind geometrische und physikalische Eigenschaften einfacher Leitungen bekannt, so kann mithilfe von Formelsammlungen die Leitungsimpedanz Z in guter Näherung berechnet werden. Im Labor können die hauptsächlichen Leitungseigenschaften mit einer automatischen R-L-C-Messbrücke mit zwei Messungen bei höherer Frequenz ermittelt werden. Die Wellenlänge der Messfrequenz muss sehr viel größer als die Länge des Leiterstücks sein. Eine Messung erfolgt bei offenem Leitungsende, wobei sich die Leitung kapazitiv verhält. Die andere Messung wird bei gleicher Frequenz und kurzgeschlossenem Leitungsende durchgeführt. Zusätzlich kann der ohmsche Schleifenwiderstand mit einem DC-Signal gemessen werden. Mit den Ergebnissen der AC-Messungen kann die Leitungsimpedanz berechnet werden: \[Z = \sqrt {{Z_{offen}} \cdot {Z_{kurz}}} \]
Experimentelle Bestimmung des Wellenwiderstands einer Leitung
Die Messungen erfolgten an einer 19 m langen flachen Verlängerungsleitung aus Kupferlitze mit einem Leiterquerschnitt von 1 mm2. Die Signalquelle war ein einstellbarer Sinusfrequenzgenerator. Die Strom- und Spannungsmessung wurden mit einem elektronischen Analogmultimeter vorgenommen. Der Hersteller garantierte die Anzeigegenauigkeit innerhalb einer 30 kHz Bandbreite für sinusförmige Signale. Eine zusätzliche Testmessreihe ergab korrekte Werte auch noch für Sinusfrequenzen bis 50 kHz. Die Bedingung, dass die Wellenlänge der höchsten Messfrequenz mit 6 km sehr viel größer als die Leitungslänge ist, war erfüllt.
Der ohmsche Schleifenwiderstand der 19 m langen Leitung wurde mittels DC-Spannungs- und Strommessungen mit kurzgeschlossenem Leitungsende rechnerisch zu 0,45 Ω bestimmt. Dieser Wert hätte auch aus der Leiterlänge, dem Leiterquerschnitt und der Leitfähigkeit von Kupfer errechnet werden können. Die kapazitive Leitungseigenschaft wurde bei offenem Leitungsende gemessen. Die Tabelle zeigt die Werte der gleichzeitigen Spannungs- und Strommessung am Leitungseingang. Der ohmsche Schleifenwiderstand hat bei offener Leitung keinen Einfluss.
| f/kHz | U/V | I/mA | Z/kΩ | C/nF |
|---|---|---|---|---|
| 5 | 5 | 0,188 | 26,60 | 1,20 |
| 10 | 5 | 0,360 | 13,90 | 1,14 |
| 15 | 5 | 0,530 | 9,43 | 1,13 |
| 20 | 5 | 0,715 | 6,99 | 1,14 |
| 25 | 5 | 0,875 | 5,71 | 1,11 |
| 30 | 5 | 1,100 | 4,55 | 1,17 |
| 35 | 5 | 1,270 | 3,94 | 1,15 |
| 40 | 5 | 1,460 | 3,42 | 1,16 |
| 45 | 5 | 1,650 | 3,03 | 1,17 |
| 50 | 5 | 1,810 | 2,76 | 1,15 |
Die induktive Leitungseigenschaft wurde mit kurzgeschlossenem Leitungsende durch gleichzeitige Spannungs- und Strommessung durchgeführt. Bei der Berechnung des induktiven Blindwiderstands wurde der ohmsche Schleifenwiderstand berücksichtigt. Die Tabelle zeigt die Mess- und Rechenwerte.
| f/kHz | U/mV | I/mA | Z/Ω | XL/Ω | L/μH |
|---|---|---|---|---|---|
| 5 | 50 | 78,5 | 0,637 | 0,451 | 14,35 |
| 10 | 50 | 52,3 | 0,956 | 0,843 | 13,42 |
| 15 | 100 | 75,0 | 1,333 | 1,255 | 13,32 |
| 20 | 100 | 58,0 | 1,724 | 1,664 | 13,24 |
| 25 | 100 | 46,8 | 2,137 | 2,089 | 13,30 |
| 30 | 100 | 39,3 | 2,545 | 2,505 | 13,29 |
| 35 | 100 | 33,5 | 2,990 | 2,956 | 13,44 |
| 40 | 100 | 26,8 | 3,730 | 3,703 | 14,73 |
| 45 | 100 | 23,0 | 4,348 | 4,325 | 15,30 |
| 50 | 100 | 20,0 | 5,000 | 4,98 | 15,85 |
Mit diesen Ergebnissen errechnet sich ein durchschnittlicher Kapazitätswert zu 1,15 nF und ein durchschnittlicher Induktivitätswert zu 14 μH. Der Isolationswiderstand der Leitung konnte nicht gemessen werden. PVC oder Silikonkautschuk hat einen durchschnittlichen spezifischen Widerstand von 10 TΩ·m. Manchmal wird bei online Berechnungsprogrammen ein Ableitungswert von G' = 0,1μS/km vorgegeben. Das entspricht einem Isolations-Belagswert von 10 GΩ/m. Der Isolationswiderstand ist umgekehrt proportional zur Leiterlänge.
Die untersuchte Leitung hat die durchschnittlichen Belagswerte: Widerstandsbelag R' = 23,7 mΩ/m, Kapazitätsbelag C' = 60,53 pF/m und Induktivitätsbelag L' = 736,84 nH/m. Mit der vereinfachten Formel errechnet sich die Impedanz dieser Leitung zu: \[Z = \sqrt {\frac{{14 \cdot {{10}^{ - 6}}\,H}}{{1,15 \cdot {{10}^{ - 9}}\,F}}} = 110,34\,\Omega \] Die Durchschnittswerte aus den Messwerttabellen sind \({Z_{offen}} = 8\,k\Omega \) und \({Z_{kurz}} = 2,54\,\Omega \). Mit der weiter oben genannten Formel errechnet sich die Leitungsimpedanz zu \(Z = \sqrt {8\,k\Omega \cdot 2,54\,\Omega } = 142,5\,\Omega \). Das Ergebnis ist vergleichbar. Der ohmsche Leitungswiderstand war wirksam und auf eine Fehlerrechnung wurde verzichtet.
Für AC-Signale zeigt eine Leitung Tiefpasscharakter mit einer messbaren oberen Grenzfrequenz. Zur Messung muss sie mit einem ohmschen Widerstand abgeschlossen oder belastet sein, der den Wert der Leitungsimpedanz hat. Das vereinfachte Ersatzschaltbild zeigt unter Vernachlässigung des Ableitwiderstands eine RLC-Reihenschaltung, vergleichbar mit einem Reihenschwingkreis. Am offenen Leitungsausgang muss parallel zur Leitungskapazität eine Resonanzfrequenz messbar sein. Mit den ermittelten Belagswerten wurden mit einem Simulationsprogramm für unterschiedliche Leitungslängen die oberen Grenzfrequenzen ermittelt. Die Amplituden-Frequenzdiagramme wurden mit dem ohmschen Leitungsabschluss von 110 Ω entsprechend der (verlustfreien) Leitungsimpedanz erstellt.
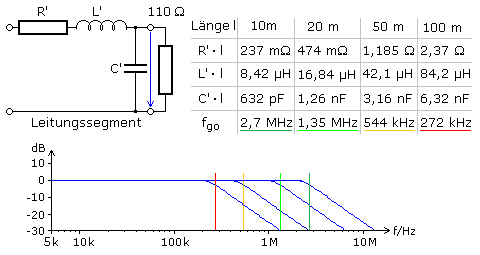
Mit offenem Leitungsende wurden die Resonanzfrequenzen per Simulation mithilfe des Amplituden-Frequenzgangs bestimmt. Für eine 10 m lange Leitung sind es 2,18 MHz während die Resonanzfrequenz für eine 100 m lange Leitung mit 218 kHz um den Faktor 0,1 kleiner ist. Die Werte entsprechen der mathematischen Berechnung mit der Schwingungsformel nach Thomson: \[{f_{res}} = {\left[ {2 \cdot \pi \cdot \sqrt {L' \cdot l \cdot C' \cdot l} } \right]^{ - 1}}\]
△Ausbreitungsgeschwindigkeit und Wellenlänge
Liegt am Eingang einer homogenen Leitung Wechselspannung als elektromagnetisches Signal, so bewegt sich die Spannungs- und Stromwelle mit einer bestimmten Ausbreitungsgeschwindigkeit zum Leitungsende. Licht hat die Eigenschaft einer elektromagnetischen Welle und breitet sich im Vakuum mit der höchsten in der Natur beobachteten Lichtgeschwindigkeit aus. Die Signallaufzeit einer elektromagnetischen Welle entlang einer Leitung ist von den Eigenschaften der Leitung abhängig. Hier ist es insbesondere die elektrische Feldkonstante \({\varepsilon _o}\) auch Influenzkonstante oder Permittivität des Vakuums und die magnetische Feldkonstante oder magnetische Permeabilität \({\mu _o}\). Hinzu kommen als Multiplikatoren \({\varepsilon _r}\) und \({\mu _r}\). Es sind benennungslose relative Eigenschaften des Ausbreitungsmediums, die im Vakuum den Wert 1 haben. Ist ein elektrischer Leiter mit einem nichtleitenden Werkstoff isoliert, dann ist \({\varepsilon _r} > 1\). Für nicht ferromagnetische Werkstoffe unterscheiden sich die magnetischen Permeabilitätswerte erst ab der vierten Stelle nach dem Komma. Für sie gilt in sehr guter Näherung weiterhin \({\mu _r} \approx 1\).
Für eine verlustfreie homogene Leitung ist das Produkt L'·C' von der Leitungsgeometrie unabhängig. Mit den Proportionalitäten \(L' \propto {\mu _o} \cdot {\mu _r}\) und \(C' \propto {\varepsilon _o} \cdot {\varepsilon _r}\) kann folgendes geschrieben werden: \[L'\,C' = {\mu _o}\,{\mu _r}\,{\varepsilon _o}\,{\varepsilon _r}\quad \Rightarrow \sqrt {L'\,C'} = \sqrt {{\mu _o}\,{\mu _r}\,{\varepsilon _o}\,{\varepsilon _r}} \] Die Lichtgeschwindigkeit kann mithilfe der Naturkonstanten \({\varepsilon _o}\) und \({\mu _o}\) wie folgt berechnet werden: \[{\varepsilon _o} = \frac{1}{{{\mu _o}\,c_o^2}}\quad \Rightarrow {c_o} = \frac{1}{{\sqrt {{\varepsilon _o}\,{\mu _o}\,} }}\] Diese Gleichungen können zusammengefasst auch geschrieben werden als: \[\frac{1}{{\sqrt {L'\,C'} }} = {c_o}\frac{1}{{\sqrt {{\mu _r}\,{\varepsilon _r}} }}\] Auf der rechten Seite der Gleichung steht die Lichtgeschwindigkeit \({c_o}\) in m/s multipliziert mit einem benennungslosen Faktor. Der Ausdruck links des Gleichheitszeichens muss ebenfalls die Benennung einer Geschwindigkeit haben. Die Einheitengleichung zeigt, dass diese Aussage richtig ist: \[\frac{1}{{\sqrt {\frac{H}{m} \cdot \frac{F}{m}} }} = \frac{1}{{\sqrt {\frac{{V\,s}}{{m\,A}} \cdot \frac{{A\,s}}{{m\,V}}} }} = \frac{1}{{\sqrt {\frac{{{s^2}}}{{{m^2}}}} }} = \frac{m}{s}\] Für ein monochromatisches Signal, ein Signal mit einer konstanten Frequenz wird dieser Ausdruck als Phasengeschwindigkeit bezeichnet. Sie kann bei Kenntnis der Belagswerte mithilfe der folgenden Formel berechnet werden: \[v = \frac{1}{{\sqrt {L'\,C'} }}\] Die Phasengeschwindigkeit ist kleiner als die Lichtgeschwindigkeit. In Datenblättern wird oft das Geschwindigkeitsverhältnis als sogenannter Verkürzungsfaktor VKF (in älterer Literatur als k) angegeben. Für die meisten Koaxialleitungen liegen die Werte zwischen 0,65 ... 0,85. \[VKF = \frac{v}{{{c_o}}} = \frac{1}{{\sqrt {{\mu _r}\,{\varepsilon _r}} }} \approx \frac{1}{{\sqrt {{\varepsilon _r}} }}\]
Im Vakuum kann für jede Periodendauer T einer elektromagnetischen Welle durch Multiplikation mit der Lichtgeschwindigkeit \({c_o}\) die zugehörige Wellenlänge λ berechnet werden. Ein Signal gleicher Periodendauer und Frequenz ist entlang einer isolierten Leitung mit einem Dielektrikum \({\varepsilon _r} > 1\) langsamer und die Wellenlänge ist kürzer. \[\lambda = T \cdot {c_o} = \frac{{{c_o}}}{f} = \frac{{{c_o}}}{{f\sqrt {{\mu _r}\,{\varepsilon _r}} }}\] \[\lambda \approx \frac{{{c_o}}}{{f\sqrt {{\varepsilon _r}} }}VKF \cdot \frac{{{c_o}}}{f}\]
Sind die am Leitungseingang eingespeiste Signalfrequenz und der Verkürzungsfaktor der Leitung bekannt, so kann mit einem Oszillograph die Leitungslänge bestimmt werden. Wird am Leitungseingang ein monochromatisches Signal eingespeist, dann kann aus dem Phasenversatz zwischen dem Ein- und Ausgangssignal der Verkürzungsfaktor bestimmt werden. Für die im Labor untersuchte Verlängerungsleitung errechnet sich die Ausbreitungsgeschwindigkeit mit den gemessenen Belagswerten zu: \[v = \frac{1}{{\sqrt {L'\,C'} }} = \frac{1}{{\sqrt {737 \cdot {{10}^{ - 9}} \cdot 60,5 \cdot {{10}^{ - 12}}} }} = 1,5 \cdot {10^8}\,\frac{m}{s}\] Der Verkürzungsfaktor kann errechnet werden und daraus die relative Permittivität der Isolierung: \[VKF = \frac{v}{{{c_o}}} = \frac{{1,5 \cdot {{10}^8}}}{{3 \cdot {{10}^8}}} = 0,5\quad \Rightarrow {\varepsilon _r} = \frac{1}{{VK{F^2}}} = 4\] Kabelisolierungen mit dem Werkstoff Polyvinylchlorid PVC und den VDE-Kurzzeichen Y, YK, YOE haben diesen Wert. Die Vakuum-Wellenlänge eines 1 MHz-Signals beträgt λo = 300 m und hätte auf dieser Leitung mit λ = 150 m eine kürzere Wellenlänge.
Mit den im Laborversuch ermittelten Leitungswerten wurde im Simulationsprogramm für zwei Leitungslängen die Laufzeit ermittelt. Die Leitung war am Ein- und Ausgang mit einem ohmschen Widerstand abgeschlossen. Zur Verhinderung jeglicher Reflexionen entlang der Leitung hatte er den Wert der Leitungsimpedanz. Am Eingang wurde ein 1 MHz Sinussignal eingespeist. Die Laufzeit zwischen dem Ein- und Ausgangssignal wurde mit einem Oszillograph ermittelt.
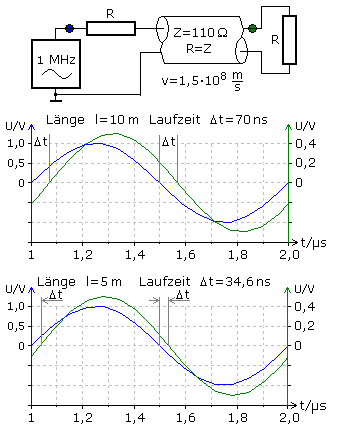
Mit dem zuvor berechneten Verkürzungsfaktor und den beiden im Simulationsversuch ermittelten Laufzeiten kann die Leitungslänge berechnet werden. \[VKF = \frac{v}{{{c_o}}}\quad v = \frac{{\Delta l}}{{\Delta t}}\quad \Rightarrow \Delta l = \Delta t \cdot {c_o} \cdot VKF\] Zur Simulation wurden die Bauteilwerte für eine 10 m und 5 m eingesetzt. Die Auswertung der Messergebnisse bestätigen, dass mit dieser Methode unbekannte Leitungslängen recht gut bestimmt werden können: \[\begin{array}{l} \Delta l = 70 \cdot {10^{ - 9}} \cdot 3 \cdot {10^8} \cdot 0,5 = 10,5\;m\\ \Delta l = 34,6 \cdot {10^{ - 9}} \cdot 3 \cdot {10^8} \cdot 0,5 = 5,19\;m \end{array}\]
△Reflexionsmessungen
Ist das Leitungsende mit dem ohmschen Wert des Wellenwiderstands abgeschlossen (belastet), so wird die ankommende Signalenergie vollkommen umgewandelt. Bei einem größeren oder kleineren Leitungsabschluss entsteht am Leitungsende ein neues Spannungs-/Stromverhältnis. Der Leitungsausgang wirkt wie eine Signalquelle und sendet ein Reflexionssignal mit einer bestimmten Amplitude zum Eingang zurück. Die Phasenlage zwischen der am Leitungsende ankommenden und dort reflektierten Signalwelle wird vom Wert des Abschlusswiderstands bestimmt. Die reflektierte Welle wandert mit der gleichen Phasengeschwindigkeit zum Leitungseingang zurück. Während der Reflexion entsteht entlang der Leitung eine sogenannte Stehwelle. Sie hat die maximale Amplitude beim offenen oder kurzgeschlossenen Leitungsende. Die Signalreflexion ist mithilfe einer Simulation und Videoclips auf einer anderen Seite dieses Webprojekts noch ausführlicher beschrieben.
An der im Labor untersuchten Leitung wurden Reflexionsmessungen durchgeführt. Sie wurden später angepasst für ein Simulationsprogramm bestätigt. Das Eingangssignal ist ein Rechtecksignal mit der Frequenz 1 MHz und dem Tastgrad D = 10%. Das Leitungsende ist mit einem einstellbaren Widerstand abgeschlossen. Das Quellensignal (blau) vor dem Eingangswiderstand dient als Referenz. Die Reflexionssignale (grün) wurden direkt am Leitungseingang mit einem Oszillograph gemessen. Ist der Abschlusswiderstand auf fehlendes oder minimales Reflexionssignal eingestellt, so entsprach sein Wert der mathematisch ermittelten Leitungsimpedanz. Das folgende Bild zeigt die Schaltung und die Messergebnisse für drei unterschiedliche Belastungen.
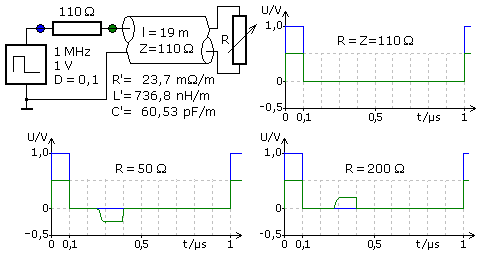 △
△
Der Skin-Effekt
In diesem Abschnitt sind die Vektorgrößen in hervorgehobener Schriftart dargestellt. Liegt Gleichspannung an einem Leiter an, so fließt nach dem ohmschen Gesetz im Leiter ein konstanter Gleichstrom. Im elektrischen Feld ist Gleichspannung die Potenzialdifferenz auf einem Wegabschnitt entlang einer Feldlinie. Die Ursache des Stroms ist eine auf den Leiter wirkende proportionale elektrische Feldstärke E. Im homogenen metallischen Leiterquerschnitt fließt ein gleichmäßig verteilter Gleichstrom. Alle Strompfade durch die Querschnittsfläche A ergeben die vektorielle Stromdichte J. Jeder Strompfad ist von einem konzentrischen Magnetfeld umgeben. Entlang des Leiterrands erreicht die magnetische Feldstärke H den höchsten Wert. Außerhalb des Leiters nimmt H(r) umgekehrt proportional mit dem Abstand r ab. Entlang des Leiters ist ein zeitlich konstantes magnetisches Gleichfeld nachweisbar.
Der Skin-Effekt entsteht im Leiter durch sich periodisch ändernde Feldgrößen, also Wechselwirkungen zwischen elektrischen und magnetischen Feldänderungen. Ein sich zeitlich ändernder Wechselstrom erzeugt im Leiter um jeden Strompfad ein konzentrisches magnetisches Wechselfeld. Wird senkrecht zur H-Feldrichtung eine geschlossene Fläche angenommen, dann ist die Dichte der magnetischen Feldlinien durch diese Fläche gleich der vektoriellen magnetischen Flussdichte B. Sie wird als magnetische Induktion bezeichnet. Beide zeitabhängige Größen H und B haben den gleichen Richtungssinn. Im Leiter entstehen in sich geschlossene Wirbelstrompfade. Nach dem Energieerhaltungssatz und der Lenz'schen Regel muss der Induktionsstrom dem primären Erregerstrom entgegen wirken. Auf der Seite zu den Größen eines Magnetfelds sind mehr mathematisch basierte Erklärungen zu finden.
Zur besseren Übersicht zeigt die Skizze nur einen Strompfad (rot) in der Leitermitte. Er ist konzentrisch vom Magnetfeld umgeben, von der nur eine Magnetfeldlinie H eingezeichnet ist. Die magnetische Feldstärke nimmt mit zunehmendem Abstand zum erzeugenden Strompfad ab. Das sich zeitlich ändernde Magnetfeld H ist proportional zur magnetischen Flussdichte B. Beide Felder haben die gleiche Richtung. Der magnetische Fluss Φ ist das Skalarprodukt aus B, einem grau eingezeichneten Flächenelement und dem Cosinus seines Anstellwinkels im H-Feld. Die maximale magnetische Flussdichte ergibt sich, wenn dieses graue Flächenelement senkrecht zum H-Feld steht. Die Ableitung dΦ/dt ist die Induktionsspannung, die nach der Lenz'schen Regel ein negatives Vorzeichen haben muss. Das E-Feld ist ein Rotationsfeld. Es erzeugt in gleicher Feldrichtung geschlossene sekundäre Strompfade. Zwei davon sind als orange Wirbelstrompfade eingezeichnet.
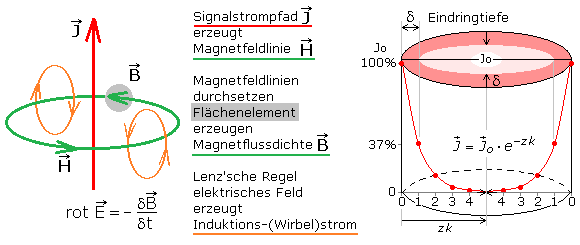
Es ist zu erkennen, dass im inneren Leiterbereich die Wirbelstrompfade entgegen der primären Erregerstromrichtung verlaufen. Im äußeren Leiterbereich weisen sie in Richtung des Primärstroms. Es findet eine Stromverdrängung zur Leiteroberfläche hin statt. Vom Außenrand zum Zentrum des Leiters nimmt die effektive Stromdichte nach einer e-Funktion ab. Der Abstand vom Außenrand des Leiters zur Leitermitte ist z und k der Dämpfungsfaktor.
Eindringtiefe / Skin-Tiefe
Für gute Leiter wird eine äquivalente Leitschichtdicke oder Skin-Tiefe δä (delta), (englisch: skin depth) definiert, wobei das Formelzeichen \(\delta \) meist ohne Index geschrieben wird. Die Skin-Tiefe ist von der elektrischen Leitfähigkeit σ (κ) des Leiters, seiner magnetischen Permeabilität μ und der Signalfrequenz f abhängig. Die theoretische Elektrophysik leitet für die Stromdichteverteilung und den Dämpfungsfaktor k folgende Formel her: \[\overrightarrow J = {\overrightarrow J _o} \cdot {e^{ - z\,k}}\quad \quad k = \sqrt {\frac{{\omega \,\mu \,\sigma }}{2}} = \sqrt {\pi \,f\mu \,\sigma } \] Der reziproke Wert von k ist die äquivalente Leitschichtdicke oder Skin-Tiefe. \[\delta = \frac{1}{k} = \frac{1}{{\sqrt {\pi \,f{\mu _o}\,{\mu _r}\,\sigma } }}\] Für nicht magnetisierbare Leiter kann \({\mu _r} = 1\) gesetzt werden. In der Formel ist \({\mu _o} = 4 \cdot \pi \cdot {10^{ - 7}}\) Vs/Am, σ (κ) die spezifische Leitfähigkeit in 1/(Ω·m) und f die Signalfrequenz. Für Rundleiter mit r » δ ist die Eindringtiefe δ der Wert, bei der die Stromdichte um den Faktor 1/e niedriger ist. Dann fließen noch 63% der auf den Außenrand normierten Stromdichte Jo = 1 innerhalb der im Bild oben skizzierten Ringfläche. Zur Leitermitte hin nimmt die Stromdichte exponentiell weiter ab. Die Tabelle zeigt für drei metallische Leiter für 1/e = 37% die Skin-Tiefe in Abhängigkeit der Signalfrequenz.
| 50 Hz | 5 kHz | 500 kHz | 5 MHz | 50 MHz | 500 MHz | σ S/m | |
| Silber | 9,11 mm | 0,91 mm | 91,1 μm | 28,8 μm | 9,11 μm | 2,88 μm | 61·106 |
| Kupfer | 9,35 mm | 0,94 mm | 93,5 μm | 26,6 μm | 9,35 μm | 2,96 μm | 58·106 |
| Aluminium | 11,7 mm | 1,17 mm | 117 μm | 37,0 μm | 11,7 μm | 3,70 μm | 37·106 |
Bei Gleichspannung fließt der Strom homogen durch eine gewählte Querschnittsfläche. Der Drahtwiderstand wird nach dem ohmschen Gesetz berechnet und ist nur von der elektrischen Leitfähigkeit \(\sigma \;(\kappa )\), dem Querschnitt A und der Leiterlänge l abhängig. Bei Wechselspannung und zunehmender Frequenz gewinnt der Skin-Effekt an Wirksamkeit. Für die Eindringtiefe besteht die Proportionalität: \(\delta \propto 1/\sqrt f \). Mit zunehmender Frequenz verringert sich die Kreisringfläche für die Strompfade. Sie werden von der Leitermitte zur Leiteroberfläche verdrängt. Für einen Rundleiter mit gegebenem Radius kann ein Zusammenhang zwischen der Skin-Tiefe δ und der Frequenz hergeleitet werden. Zwischen der Kreisringfläche und der Eindringtiefe besteht folgender Zusammenhang: \[\begin{array}{l} {A_\delta } = \pi \,{r^2} - \pi \,r_i^2 = \pi (r + {r_i})(r - {r_i})\\ \delta = r - {r_i}\quad \Rightarrow {r_i} = r - \delta \\ {A_\delta } = \pi (2\,r - \delta )\,\delta \quad mit\quad \delta \ll r\\ {A_\delta } \approx 2\,\pi \,r\,\delta \end{array}\]
Bei Wechselspannung mit konstanter Amplitude ist der Wechselstromwiderstand Rskin eines Leiters wegen des Skin-Effekts bei höheren Frequenzen größer. Mit der vereinfachten Annahme, dass der Wechselstrom bei der Eindringtiefe δ nur die Kreisringfläche nutzt, wird in der bekannten Widerstandsformel anstelle A des Massivleiters die hergeleitete Kreisringfläche Aδ eingesetzt. Der frequenzabhängige Widerstand Rskin berechnet sich mithilfe der Formel: \[{R_{skin}} = \frac{l}{{{A_\delta }\,\sigma }} = \frac{l}{{\sigma \,2\,\pi \,r}}\sqrt {\pi \,f{\mu _o}{\mu _r}\sigma } \] Die folgende Tabelle zeigt für zwei Kupferdrähte der Länge l = 1 m mit dem Radius r1 = 0,5 mm und r2 = 0,05 mm sowie μr = 1 die an der Eindringtiefe δ berechneten frequenzabhängigen Werte. Die Gleichstromwiderstände errechnen sich zu RDC1 = 22 mΩ und RDC2 = 2,2 Ω.
| Frequenz | 50 Hz | 5 kHz | 50 kHz | 0,5 MHz | 5 MHz | 50 MHz | 0,5 GHz |
| Rskin1 / mΩ | 0,587 | 5,87 | 18,6 | 58,7 | 185,7 | 587 | 1857 |
| Rskin2 / Ω | 0,0059 | 0,059 | 0,186 | 0,587 | 1,857 | 5,872 | 18,57 |
Für niedrige Frequenzen ist der Drahtwiderstand RDC die bestimmende Größe und der Skin-Effekt kann vernachlässigt werden. Ein 1 m langer Cu-Draht mit dem Radius 0,5 mm hat den ohmschen Widerstand 22 mΩ. Für den Draht errechnet sich die Eindringtiefe bei 5 kHz zu 0.94 mm. Der mit dem Skin-Effekt verbundene Widerstand beträgt aufgerundet Rskin = 6 mΩ.
Die Tabelle zeigt, dass bei einem kleineren Drahtdurchmesser der Einfluss des Skin-Effekts in den höheren Frequenzbereich verschoben ist. Aus diesem Grund werden Spulen für den Hochfrequenzbereich der Sende- und Empfangstechnik nicht mit Volldraht, sondern mit HF-Litze gewickelt. Sie besteht aus vielen sehr dünnen, einzeln mit Lack isolierten Adern, die zum Teil nach einem bestimmten System verseilt sein können und eine Außenisolierung haben. Früher war das eine Seidenumspinnung. Am Anschlusspunkt müssen alle Einzeladern gemeinsam leitend erfasst werden. Durch das Parallelschalten aller Einzeladern bleibt der ohmsche Widerstand klein. Für die Eindringtiefe ist die wirksame Oberfläche viel größer. Die Güte einer Spule ist umgekehrt proportional zum ohmschen Widerstand. Eine mit HF-Litze gewickelte Spule hat verglichen mit einer aus Volldraht gewickelten Spule mit gleichem ohmschen Widerstand in HF-Anwendungen eine höhere Güte, da sich der Skin-Effekt erst ab sehr hohen Frequenzen negativ auswirkt.
Für alle Menschen, die sich tiefergehend mit dem Skin-Effekt und den möglichen Auswirkungen beschäftigen wollen oder müssen, sollten die Maxwell Gleichungen, die zugehörige höhere Mathematik zur Berechnung der Differenzialgleichungen wirklich verstehen und anwenden können. Wie wäre es mit einem Studium der theoretischen Physik im Fachbereich Elektronik? Das ist weder mein Gebiet noch mein Aufgabenziel.
Proximity Effekt
Das englische Wort proximity bedeutet Nähe. Der Proximity Effekt beschreibt eine von der Frequenz abhängige Stromverdrängung für nahe beieinander verlaufenden Leitern, die von Wechselstrom durchflossen werden. Der Effekt ist besonders ausgeprägt bei hohen Frequenzen. Der durch den einen Leiter A fließende Strom generiert um sich herum ein Magnetfeld. Die Feldänderungen verursachen ein dynamisches elektrisches Feld und wie anfangs ausgeführt nach der Lenz'schen Regel folgen Wirbelströme. Je nach Betrachtung dringen Anteile des B-Felds oder der Wirbelströme in den oder die Parallelleiter ein und interagieren mit den dort vorhandenen dynamischen Feldgrößen. Die Wirbelströme sind nicht wie beim Skin-Effekt rotationssymmetrisch zum Leitermittelpunkt. Bildlich vorgestellt generieren die einwirkenden Magnetfeldlinien senkrecht zur Eintrittsrichtung Wirbelstrombereiche, die zu einem Wirbelstromring in Leiterlängsrichtung führen. In den nahe beieinanderliegenden Leiterinnenseiten fließt der Erregerstrom im Leiter A und der Wirbelstrom im Leiter B in gleicher Richtung. In der zum Leiter A weiter entfernten Außenseite Leiters B fließt der Wirbelstrom dem Erregerstrom entgegen.
Ein entsprechender Vorgang kann für einen Erregerstrom im Leiter B gemacht werden, der mit seinem äußeren Magnetfeld auf den Leiter A wirkt und dort einen in Leiterrichtung verlaufenden gesamten Wirbelstromring generiert. Verlaufen beide Erregerströme in entgegengesetzter Richtung, dann wird die Stromdichte im Bereich der Leiterinnenseiten größer und im Außenbereich geringer. Ist die Erregerstromrichtung in beiden Leitern gleich, dann verringert sich die Stromdichte an den direkt benachbarten Kanten und vergrößert sich nach außen. In beiden Fällen verringert sich der für den Stromfluss effektiv wirksame Leiterquerschnitt und die Impedanz nimmt zu.