Signalausbreitung auf Leitungen

Der Sinn und Zweck von Informationen ist ihre Verbreitung, wozu Informationsträger notwendig sind. Ein Stein, der ins Wasser fällt, erzeugt ein Wellenbild, das sich von Eintauchort wegbewegt. Schlägt man ein gespanntes Seil an, so ist nach einer gewissen Laufzeit am Seilende eine Auslenkung zu verspüren, die sich eine Zeit lang abschwächend periodisch wiederholt. Die Schwingungen einer Glocke oder die Membranauslenkungen eines Lautsprechers übertragen sich auf das Medium Luft. In größerer Entfernung ist der Schall dann um einige Zeit verzögert hörbar. Ein elektrisches Signal wird im oder entlang eines elektrischen Leiters übertragen, kann sich aber auch als elektromagnetische Welle im Vakuum ausbreiten.

Von der mechanischen Welle ausgehend und der Wellengleichung linearer Transversalwellen wird eine Verbindung zu elektromagnetischen Wellen auf einer Leitung hergestellt. Die dabei möglichen Reflexionen auf einer Leitung werden erklärt und auch in einem Videoclip gezeigt. Abschließend werden mittels Grafik und Formeln das Stehwellenverhältnis und der Reflexionsfaktor dargestellt.

Die mechanische Welle

Die Entstehung und Ausbreitung einer mechanischen Welle ist im physikalischen Versuchsaufbau der Wellenmaschine gut darstellbar. Als Voraussetzung gilt, dass es einen materiellen Träger gibt. Zwischen den Teilchen des Trägers besteht eine elastische Kopplung, die oftmals auf intermolekularen Kräften beruht. Lenkt man ein Trägerteilchen an seinem Ort aus, so wird das Nachbarteilchen wegen der gegenseitigen elastischen Kopplung zeitversetzt in die gleiche Richtung ausgelenkt. Das regt dann in Fortsetzung seinen nächsten Nachbarn an. Führt das erste Erregerteilchen eine stetige Schwingung um seinen Ruheort aus, so beobachtet man eine Wellenbewegung. Nach einer vollen Schwingungsdauer des Erregerteilchens hat sich die Welle aufgrund der elastischen Kräftekopplung um eine bestimmte Strecke fortbewegt. Dieser Weg entspricht der Wellenlänge λ, dem Abstand benachbarter Teilchen, die sich im gleichen Schwingungszustand oder gleicher Phasenlage befinden.

Kommt das Erregerteilchen, die eigentliche Informationsquelle, zur Ruhe, so befinden sich nach einiger Zeit alle Teilchen wieder am ursprünglichen Ruheort. Nur die Informationsenergie hat sich vom Ort der Erregung auf oder im Träger weiter bewegt. Schwingen die Teilchen senkrecht zur Ausbreitungsrichtung wie bei einer schwingenden Saite, einer Seilwelle oder Wasserwelle, so entstehen Transversalwellen. Verläuft die Ausbreitungsrichtung parallel zur Schwingungsebene der Teilchen, wie bei einer Spiralfeder oder der Schallausbreitung, so entstehen Longitudinalwellen.

Wellengleichung linearer Transversalwellen

Das Erregerteilchen, in der Elektronik die Elektronen der Signalquelle oder des Oszillators, soll um ihren Ruheort sinusförmige Schwingungen ausführen. Die Nachbarteilchen erfahren die Auslenkung der Schwingung entsprechend zeitverzögert. Die Amplitude der Wellenbewegung ist in Abhängigkeit vom Ort x und der Zeit t zu betrachten. Die Wellengleichung ergibt sich daraus wie folgt:

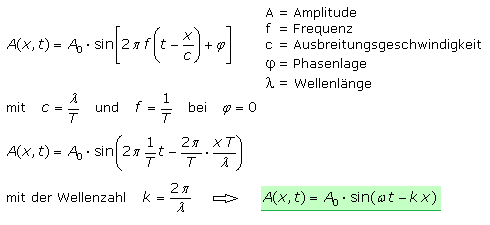
Die Wellenzahl k steht für die Anzahl der Wellen, die sich auf der Ausbreitungsstrecke x befinden. Die Angabe erfolgt im physikalisch nicht mehr gebräuchlichen Maßsystem cm⁻¹. Werden auf dem Wellenzug entlang der Ausbreitungsrichtung alle Punkte mit gleichem Phasenzustand betrachtet, kann daraus die Ausbreitungsgeschwindigkeit c der Welle berechnet werden. Das Verhältnis aus dem kürzesten Weg und der zugehörigen Zeit für den gleichen Phasenzustand wird als Phasengeschwindigkeit bezeichnet.

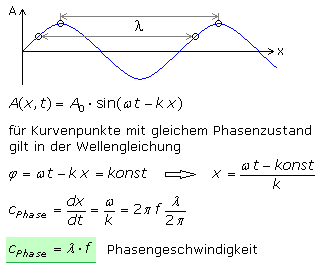
Die Phasengeschwindigkeit ist bei konstanter Frequenz vom Ausbreitungsmedium abhängig. Für elektromagnetische Wellen im Vakuum entspricht sie der Lichtgeschwindigkeit c ≈ 3·10⁸ m/s. Die Schallausbreitung in Luft beträgt c ≈ 340 m/s, während sie im Wasser mit c ≈ 1480 m/s wesentlich schneller ist. Für eine gegebene Frequenz errechnen sich vom Medium abhängig unterschiedliche Wellenlängen.

Eine Tonfrequenz kann im Kundtschen Rohr, bekannt aus dem Physikunterricht, durch die Dichteverteilung von Korkmehl messbar gemacht werden. Der Abstand gleicher Dichteverteilungen entspricht beim einseitig geschlossenen Rohr der halben Wellenlänge. Ein Ton mit 10 kHz hat in Luft eine Wellenlänge von rund 3,4 cm. Für die gleiche Frequenz beträgt die Wellenlänge im Wasser rund 15 cm.

Diese niedrige 10 kHz Frequenz als elektromagnetische Welle über eine Antenne abzustrahlen ist praktisch nicht sinnvoll. Die Antenne sollte ein Halbwellendipol sein, der dann eine Länge von 15 km haben müsste. Das UKW-Rundfunkband hat eine Mittenfrequenz von 98 MHz und die zugehörige Wellenlänge beträgt etwa 3 m. Eine Stabantenne mit 1,5 m entspricht dem Halbwellendipol und gewährleistet guten Empfang.

Die Entstehung und Ausbreitung einer Transversal- oder Querwelle ist im ersten Teil des später gezeigten Videoclips zu sehen. Er zeigt die Wellenbewegung nach der aus dem Physiklabor bekannten Wellenmaschine. Die einzelnen erregten Teilchen schwingen senkrecht zu festen Ortsparametern. Für eine konstante Erregerfrequenz zeigt die Animation die fortschreitende Welle bei einfacher und doppelter Weglänge.

Elektromagnetische Wellen auf einer Leitung

Mit dem Modell der mechanischen Welle ist auch die Signalübertragung elektromagnetischer Wellen im elektrischen Leiter erklärbar. Der elektrische Impuls oder die Information wird mit nahezu Lichtgeschwindigkeit c0 übertragen. Der Stromkreis benötigt eine Hin- und Rückleitung, die insgesamt über ohmsche, induktive und kapazitive Eigenschaften verfügt. Die theoretisch mathematischen Grundlagen sind im Kapitel Leitungen und ihre Eigenschaften dargelegt. Die Signalgeschwindigkeit ist abhängig von der relativen Dielektrizitäts- oder Permittivitätszahl εr des Isolationsmaterials zwischen dem Adernpaar. Die Ausbreitungsgeschwindigkeit ist kleiner als die Lichtgeschwindigkeit, die nur in der Luft oder im Vakuum erreicht wird. Für Koaxialleitungen liegt der Verkürzungsfaktor zwischen K = 0,65 ... 0,85.

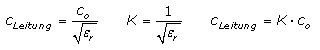
Jede Leitung hat einen Wellenwiderstand, die Leitungsimpedanz. Dieser Wert ist nicht identisch mit dem ohmschen Drahtwiderstand und kann nicht mit einem Ohmmeter gemessen werden. Mit zunehmender Signalfrequenz und bei Impulsen mit steilen Flanken ist das Einbeziehen der Leitungsimpedanz in Verbindung mit der Generator- und Verbraucherimpedanz besonders wichtig. Der ohmsche Leitungswiderstand erzeugt für alle Frequenzen lineare Verzerrungen. Bezogen auf das Eingangssignal wird mit zunehmender Leitungslänge das Ausgangssignal in der Amplitude gedämpft. Mit ihren induktiven und kapazitiven Eigenschaften wirkt jede Leitung als Tiefpass. Je höher die Eingangsfrequenz bei konstanter Leitungslänge oder je länger der Übertragungsweg bei gleicher Frequenz ist, desto weniger Oberwellenanteile weist das Ausgangssignal auf. Rechtecksignale am Eingang werden zu sinusförmigen Ausgangssignalen verschliffen.

Reflexion auf einer Leitung

Für die folgenden Betrachtungen soll der Signalgenerator am Eingang der Leitung die gleiche Impedanz wie die Leitung haben. Am Eingang besteht Leistungsanpassung und zur Vereinfachung sollen keine Energieverluste auf der Leitung auftreten. Am Leitungsende ergeben sich drei eindeutige Zustände und zwei Bereiche der Belastung, die als Leitungsabschluss bezeichnet werden.

• Der Ausgang ist mit der gleichen Impedanz belastet, die der Generator und die Leitung haben.
• Der Ausgang bleibt unbelastet und offen. Für die Abschlussimpedanz kann Z ≈ ∞ gesetzt werden.
• Der Ausgang ist kurzgeschlossen, die Abschlussimpedanz hat den Wert Z = 0 Ω.
• Die Lastimpedanz ist kleiner als die Leitungsimpedanz aber kein Kurzschluss.
• Die Lastimpedanz ist größer als die Leitungsimpedanz jedoch nicht offen.

Der erste Fall beschreibt die Leistungsanpassung. Die am Leitungsausgang ankommende Signalenergie wird vollständig umgesetzt. Das System einer Senderendstufe mit Sendedipolantenne arbeitet so. Kabelverbundene Computernetze, sowie alle Videosysteme von der Kamera über den Schnittplatz bis zum Bildschirm sind von gleicher Impedanz und folglich für Leistung angepasst. Das eingespeiste Signal durchläuft die Leitung ungestört.

Ist das Leitungsende offen und unbelastet, kann die ankommende Energie nicht umgesetzt werden. Am Leitungsende fließt zu keinem Zeitpunkt Strom. Der Spannungsverlauf entspricht dem ankommenden Signal. Die Energie kann nicht verloren gehen und muss vollständig reflektiert werden. Der Leitungsausgang verhält sich als Oszillator oder Generator und sendet das Signal auf der Leitung zum Eingang zurück.

Die Betrachtung kann für die Signalspannung und für den Signalstrom getrennt erfolgen. Ein hilfsweise angenommener, virtueller Oszillator am Ausgang erzeugt eine zum eintreffenden Signal phasengleiche Spannungswelle. Da bei offener Leitung am Ausgang kein Strom fließt, hat die Stromwelle mit der Amplitude null einen festen Knotenpunkt. Die reflektierte Stromwelle muss daher mit einem Phasensprung von 180° invertiert zum Eingang zurücklaufen.

Der Signalstrom des virtuellen Oszillators schwingt bei einer am Ausgang kurzgeschlossenen Leitung zu jedem Zeitpunkt phasengleich mit dem ankommenden Signal. Bei Kurzschluss ist am Ausgang zu keinem Zeitpunkt eine Spannung messbar. Die ankommende Spannungswelle muss folglich am Leitungsende mit 180° Phasendrehung zum Eingang reflektiert werden.

Ist der Leitungsausgang mit einem beliebigen Widerstand belastet, der nicht der Leitungsimpedanz entspricht, wird das Signal mit einer mehr oder weniger großen Amplitude vom Ausgang zum Eingang reflektiert. Alle folgenden Betrachtungen gehen von einer Impedanzanpassung am Eingang aus. Das Leitungsende wird unterschiedlich belastet. Auf der Leitung überlagern sich die hin- und rücklaufenden Spannungs- und Stromwellen. Sie bilden dort ortsfeste Wellenmuster aus, die als Stehwellen bezeichnet werden. Die Wellengleichung der Überlagerung errechnet sich durch Addition der Wellengleichungen für das Hin- und Rücksignal. Die Herleitung verwendet die Additionstheoreme für Winkelfunktionen, wobei hier entweder eine offene oder kurzgeschlossene Leitung ohne ohmsche Verluste angenommen wird.

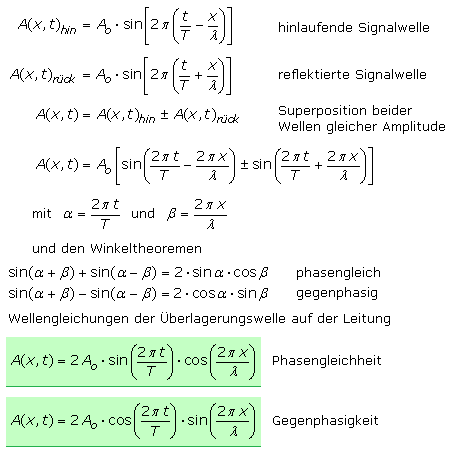
Der folgende Videoclip zeigt die beschriebenen Fälle animiert. Die individuelle Steuerung kann nur mithilfe der Controlleiste erfolgen. In einzelnen Abschnitten wird die Ausbreitung eines Sinussignals mit einfacher und doppelter Frequenz entlang einer Leitung dargestellt. Die nächsten beiden Abschnitte zeigen den Spannungs- und Stromverlauf, wenn die Leitung am Ende mit ihrer eigenen Impedanz belastet ist. Es folgen die Wellenausbreitungen für Spannung und Strom für eine am Ende offene, nicht belastete Leitung. Die nächsten beiden Abschnitte zeigen den Verlauf der Strom- und Spannungskurven beim Kurzschluss am Leitungsende.

Weitere Abschnitte im Videoclip zeigen für die Signalspannung das Reflexionsverhalten der Leitung bei den Leitungsabschlüssen: Kurzschluss, Impedanzabschluss und offene Leitung. Es folgen drei Einstellungen zum Stehwellenverhältnis bei variablem Leitungsabschluss. Für den Impedanzabschluss mit 100 Ω ist das Stehwellenverhältnis 1 und es gibt keine Reflexion und keine Stehwelle. Bei Fehlanpassung mit zu großem Lastwiderstand, hier 150 Ω wird das Stehwellenverhältnis größer und entlang der Leitung bildet sich eine Stehwelle mit dem berechneten Amplitudenverlauf aus. Bei zu kleinem Lastwiderstand, hier 50 Ω werden das Stehwellenverhältnis und die Amplitude der Stehwelle ebenfalls größer.

Stehwellenverhältnis und Reflexionsfaktor

Die am Leitungsende ankommende Energie wird bei Leistungsanpassung vollständig von der Anschlussimpedanz ZA übernommen. Eine Reflexion findet nicht statt und ein noch zu definierender Reflexionsfaktor hat seinen Minimalwert r = 0. Eine am Ausgang unbelastete oder kurzgeschlossene Leitung führt zur Totalreflexion mit dem Maximalwert r = 1. Fehlangepasste Leitungen reflektieren mit 0 < r < 1 mehr oder weniger Energie zum Eingang zurück.

Das Verhältnis aus Summe und Differenz der zum Ausgang hinlaufenden und zum Eingang rücklaufenden Effektivwerte der Wellen auf einer Leitung wird als Stehwellenverhältnis SWR oder auch VSWR, voltage standing wave ratio bezeichnet. Der Wert wird nur von der Leitung und ihrem Abschlusswiderstand bestimmt. Die Messtechnik verwendet spezielle Stehwellenmessgeräte, die das Stehwellenverhältnis oder den entsprechenden Reflexionsfaktor aus dem Spannungsverhältnis anzeigen. Bei sehr hohen Signalfrequenzen bestimmt man den Wert mithilfe Leistungsmessungen.

Ohne Reflexion, bei Leistungsanpassung am Leitungsende ergibt sich ein Stehwellenverhältnis von VSWR = 1. Bei Reflexion mit VSWR = 2 liegt eine gute Anpassung mit geringen Energieverlusten auf der Leitung vor. Werte über 5 weisen auf eine schlechte Anpassung mit großem Reflexionsanteil hin.

Die beiden Extremfälle mit Leerlauf oder Kurzschluss am Leitungsausgang ergeben eine vollständige Reflexion. Ein Kurzschluss am Leitungsausgang bewirkt einen Spannungsknoten mit dem Spannungsminimum 0 Volt. Dieser Knotenpunkt wiederholt sich entlang der Leitung bei λ/2, λ, 3λ/2 usw. während bei λ/4, 3λ/4, 5λ/4 usw. die Amplitude ihren Maximalwert hat.

Bei der unbelasteten, am Ausgang offenen Leitung befindet sich dort das Spannungsmaximum. Der erste Knotenpunkt liegt bei λ/4. Die Verhältnisse sind somit nur um eine viertel Wellenlänge verschoben. Das Stehwellenverhältnis geht für beide Extremfälle gegen unendlich. Die Leitung wirkt dann als Schwingkreis, wobei die Resonanzwellenlänge und die Frequenz von der Leitungslänge und ihrem mechanischen Aufbau bestimmt sind.

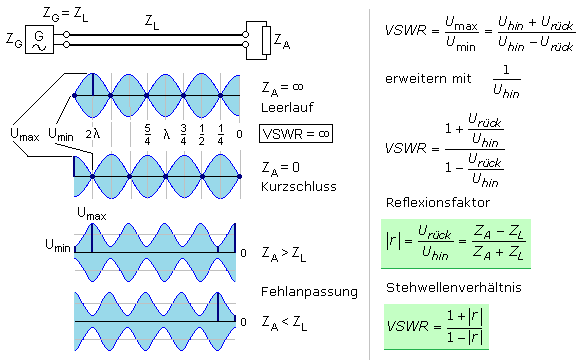
Leitungs- und Lastimpedanz bilden für das hinlaufende Signal einen Spannungsteiler. Die hinlaufende Spannung ist somit proportional zur Summe der Abschlussimpedanz ZA und der Leitungsimpedanz ZL. Die Spannung an ZA wird bei der Reflexion vom selben Spannungsteiler beeinflusst. Die zurücklaufende Spannung am Eingang ist daher proportional zur Differenz ZA − ZL. Der Reflexionsfaktor ist das vorzeichenlose Verhältnis der rücklaufenden zur hinlaufenden Signalamplitude.

Für den Leerlauf- und Kurzschlussfall bildet die Stehwelle auf der Leitung im Abstand von λ/2 ausgezeichnete Nullstellen. Bei allen anderen Fehlanpassungen gehen die Nullstellen in Amplitudenminima über. Das Amplitudenverhältnis Umax/Umin ist stets kleiner als bei den Extremfällen. Ist ZA > ZL bildet die Stehwelle am Ausgang ein Amplitudenmaximum und mit ZA < ZL entsteht dort ein Amplitudenminimum.