Der Vektoroperator Nabla
Skalarfeld
Viele Beobachtungen unserer Umwelt und experimentelle Ergebnisse versucht man durch mathematische Funktionen zu beschreiben. So verhält sich der elektrische Strom am selben ohmschen Widerstand proportional zur angelegten elektrischen Spannung. Die mathematische Funktion wird durch I = f(U) = U / R mit R als konstantem Parameter beschrieben. Entsprechend können viele Abhängigkeiten als Funktion mit einer Variablen und ein oder mehreren konstanten Parametern beschrieben werden. Der Funktionsgraph im kartesischen ebenen Koordinatensystem ist eine Kurve. Wird der Parameter bei sonst unveränderten Versuchsbedingungen geändert und grafisch dargestellt, erhält man Kurvenscharen.
Ein Skalarfeld ist eine Ansammlung von Zahlenwerten in der Ebene oder im Raum. Es sind die Werte einer Funktion, die von mehreren Variablen abhängig ist. Für das oben gegebene Beispiel kann der Wert des elektrischen Stroms, der von den Variablen U und R abhängig ist, für jedes Wertepaar berechnet und in ein nunmehr dreidimensionales kartesisches Koordinatensystem eingetragen werden. Der Stromwert zeigt sich in der Grafik dann als Höhenwert. Das Messen von Temperatur- oder Druckwerten im Raum ergibt für jeden Raumpunkt mit den Variablen (x, y, z) einen bestimmten Wert und in der grafischen Darstellung ein räumliches Skalarfeld. Die Stärke eines elektrischen Feldes kann für jeden Ort mithilfe einer dort eingebrachten Probeladung, die das Feld nicht stört, bestimmt werden.
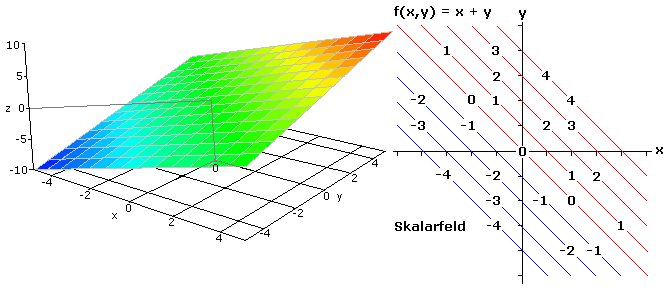
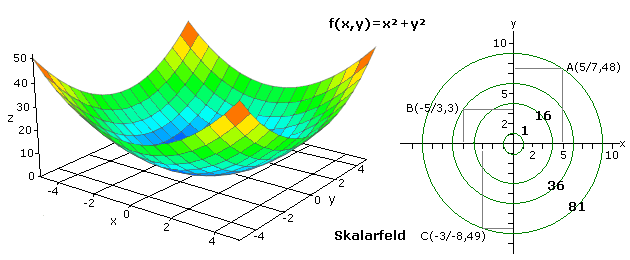
Die zwei folgenden Bilder zeigen für einfache mathematische Funktionen mit zwei Variablen ein Ausschnitt der Skalarfelder. Die räumlichen Darstellung wurde mittels einer Online-Software (https://academo.org/demos/3d-surface-plotter) erstellt und geringfügig überarbeitet. Bei der ebenen Darstellung des Skalarfelds schaut man direkt senkrecht von oben in die Richtung der z-Achse. Die mit der Funktionsgleichung errechneten Höhenwerte oder Potenziale am gewählten Ort (x, y) liegen parallel und senkrecht ober- oder unterhalb der x-y-Ebene an. Im Bildteil rechts sind die skalaren Werte in die x-y-Ebene eingetragen.
Das Höhenprofil der zweiten Funktion ist mit symmetrischen Schalen vergleichbar. Sie sind konzentrisch um den Koordinatenursprung angeordnet und haben dort den niedrigsten Wert. Mit den Punktkoordinaten errechnen sich die im rechten Bildteil eingetragenen Potenzialwerte. Die Isolinien oder Äquipotenziallinien sind die Verbindungen aller Punkte mit gleichem Höhenwert und liegen hier auf konzentrischen Kreisen.
In einem Skalarfeld ist jedem Punkt P eines ebenen oder räumlichen Bereichs einer reell wertigen Funktion eindeutig eine Zahl zugeordnet. Bei einem stationären Skalarfeld bleiben die Messwerte zeitunabhängig konstant. Werden gleiche Messwerte miteinander verbunden, so erhält man in einem zweidimensionalen Skalarfeld Niveau- oder Äquipotenziallinien, auch als Isolinien bezeichnet und im dreidimensionalen Skalarfeld Niveau- oder Äquipotenzialflächen.
Vektorfeld
Jedem Ort in der Ebene (x, y) oder im Raum (x, y, z) wird ein Vektor zugeordnet, der durch seinen Anfangs- und Endpunkt definiert ist. Im kartesischen Koordinatensystem werden die Vektoren des Vektorfelds durch die skalaren Komponenten des Vektors in den Achsenrichtungen beschrieben. Die Vektorkomponenten hängen von den Einheitsvektoren der Achsen ab.

Für ein Skalarfeld kann von einem Punkt ausgehend die Richtung zur größten Zunahme ermittelt werden. Ein Feld wird grafisch durch Feldlinien dargestellt, wobei es sich um Hilfslinien handelt, die in Richtung der wirkenden Größe zeigen. Die an einen Punkt des Vektorfelds angelegte Tangente gibt die Richtung der wirkenden Größe an. Von einer Punktladung ausgehend verlaufen die elektrischen Feldlinien radial nach außen. Es handelt sich um ein radial- oder kugelsymmetrisches Vektorfeld mit Feldvektoren in radialer Richtung und dem vom Radius abhängigen Betrag. Ein aufgeladener Plattenkondensator hat in seinem Innenbereich ein homogenes Vektorfeld, da alle Feldvektoren in die gleiche Richtung weisen und den gleichen Betrag haben. Die Vektoren stehen senkrecht auf den Isolinien oder Isoflächen.
Differenzialoperatoren – Nabla-Operator
Aussagen über das Verhalten einer Funktion mit einer Variablen lassen sich durch Bilden der Ableitungen für die Funktion machen. Der anzuwendende Operator ist der bekannte Differenzialoperator d / dx. Auf die Funktion y = f(x) angewendet erhält man die Ableitung erster Ordnung zu f '(x) = df(x) / dx. Funktionen, die von mehreren Variablen abhängig sind, können partiell (einzeln) nach jeder Variablen abgeleitet werden. Alle Komponenten, die dabei nicht von der gewählten Variablen abhängen, werden als konstante Parameter betrachtet. Partielle Differenzialoperatoren werden mit den Zeichen ∂ geschrieben. Ein einfaches Beispiel soll das verdeutlichen.

Ein wichtiger Bestandteil der Vektoranalysis ist der Differenzialoperator Nabla, auch Hamilton-Operator genannt. Der Nabla-Operator wird auch als Vektoroperator, im englischen Sprachgebrauch mit Del bezeichnet und hat als Komponenten die partiellen Differenzialoperatoren. Geschrieben wird er als ein auf der Spitze stehendes gleichseitiges Dreieck ∇ mit oder ohne Vektorpfeil. Er kann allgemein oder im kartesischen Koordinatensystem als gebundener Vektor mit den Einheitsvektoren der Achsen geschrieben werden.
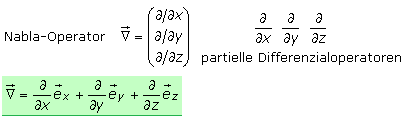
Der Nabla-Operator kann sowohl auf skalare Funktionen als auch auf Vektorfunktionen angewendet werden. Auf ein Skalarfeld angewendet, wird die Funktion partiell differenziert und man erhält mit dem Gradienten ein Vektorfeld. Nabla mit einem Vektorfeld skalar multipliziert führt als Divergenz zum zugehörigen Skalarfeld. Bei der Kreuzmultiplikation erhält man eine Aussage über den Charakter des Vektorfelds. Mit dieser als Rotation, im englischen Sprachgebrauch als curl bezeichneten Operation lässt sich feststellen, ob das Feld Quellen und Senken hat.
In einem statischen elektrischen Feld entspringen die Feldlinien in Quellen und enden in Senken, es gibt keine Wirbel. Die Divergenz eines derartigen Vektorfelds hat einen Wert ungleich null, der bei vorhandenen Quellen positiv und bei Senken negativ ist. Die Rotation des Vektorfelds ist null. Feldlinien in einem quellenfreien Wirbelfeld sind wie im Magnetfeld in sich geschlossen, da in der Natur bisher keine magnetischen Monopole bekannt sind. Die Divergenz eines Wirbelfelds hat den Wert null, während die Rotation einen Wert ungleich null hat. Die von Antennen abgestrahlten dynamischen Hochfrequenzfelder setzen sich aus elektrischen und magnetischen Wirbelfeldern mit jeweils in sich geschlossenen E- und H-Feldlinien zusammen.
Gradient
Die Steigung ist der Gradient einer Funktion, die in 1-D nur von einer Variablen abhängt. Sie wird mithilfe des bekannten Differenzialoperators bestimmt. Für Funktionen in 2-D mit zwei unabhängigen Variablen oder in 3-D mit drei Variablen kann ebenfalls die Steigung in jedem Punkt bestimmt werden. Die Funktion wird dazu partiell nach ihren Variablen abgeleitet. Das Ergebnis ist ein vom Koordinatenursprung ausgehender Vektor mit den durch die partiellen Ableitungen bestimmten Komponenten. Er wird parallel an den Ort der Punktkoordinaten verschoben und zeigt in Richtung des steilsten Anstieges des Skalarfelds. Der Betrag des Vektors steht für die Größe des Anstieges. Hat die Funktion im betrachteten Punkt einen Extremwert wie Minimum, Maximum oder ist es ein Sattelpunkt, dann ergibt der Gradient einen Nullvektor.
Der Gradient kann mit dem Nabla-Operator ∇ als Multiplikation mit der Funktion geschrieben werden. Man erhält das zum Skalarfeld zugehörige Vektorfeld, dessen Komponenten die partiellen Ableitungen des Skalarfelds sind. Für Funktionen in 2-D ist der Gradient ein ebener Vektor, der senkrecht auf den Niveau- oder Äquipotenziallinien mit f(x, y) = konst steht. Für Funktionen in 3-D steht der Gradient senkrecht auf den Äquipotenzialflächen mit f(x, y, z) = konst. Der Gradientenvektor geht vom Koordinatenursprung aus und zeigt nicht auf die absolute Lage des Maximums. Durch Einsetzen der Punktkoordinaten in die partiellen Ableitungen kann der Gradient für jeden Ort bestimmt werden. Der Betrag des Vektors gibt den Steigungswert in diesem Ort an.

Richtung der größten Steigung
Die Steigung einer Funktion mit nur einer Variablen ist für jeden Punkt durch die 1. Ableitung bestimmbar. Für Funktionen in 2-D und 3-D wird die Steigung durch einen Richtungsvektor bestimmt. Bei Funktionen mit zwei Variablen liegen alle Richtungsvektoren in der x-y-Ebene. Die Funktion hat dort einen Extrempunkt, wo die anliegende Tangente den Steigungswinkel null hat. Mathematisch ermittelt werden die Punktkoordinaten durch Nullsetzen der 1. Ableitung. Zeigt ein Vektor in die Richtung seines Einheitsvektors, dann hat der eingeschlossene Winkel den Wert 0°. Die Länge des Vektors hat in dieser Richtung ihr Maximum. Der Gradient einer differenzierbaren Funktion gibt für die Punktkoordinaten die Richtung zur maximalen Steigung an. Der Betrag des Vektors gibt die Größe der Steigung an.

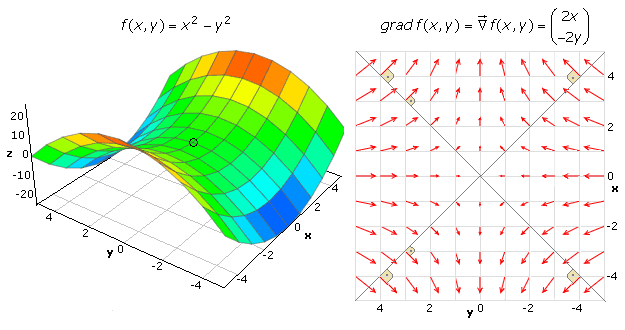
Das folgende Bild zeigt links einen Ausschnitt der Funktion f(x, y) = x² − y² um den Sattelpunkt herum, der im Koordinatenursprung liegt. Rechts ist für diesen Bereich das zugehörige Vektorfeld, der Gradient der Funktion dargestellt. Es ist ein etwas überarbeitetes Ergebnis der Online-Software (https://academo.org/demos/vector-field-plotter). Für Funktionen in 2-D liegen alle Vektoren in der x-y-Ebene. Die Diagonalen der x-y-Ebene stellen Isolinien der Höhe null dar. Man erkennt, dass die zugehörigen Vektoren immer senkrecht auf den Isolinien stehen. Sie zeigen in die Richtung der größten Steigung, aber nicht in die z-Richtung. Im Sattelpunkt liegt der Nullvektor. Entlang der x-Achse ist der Sattelpunkt der höchste Punkt. Die Vektoren zeigen dorthin, werden aber kürzer, da von außen kommend der Anstieg immer geringer wird. Vom Sattelpunkt weg in Richtung der y-Achse wird die Steigung zunehmend größer. Die Vektoren zeigen das mit ihrer Richtung und zunehmender Länge an.
Richtungsableitung
Mit der Richtungsableitung bestimmt man die Änderung eines Funktionswertes von einem Ort ausgehend in eine beliebige Wegrichtung. Die neue Richtung entspricht dem Richtungsvektor. Zur Bestimmung der Richtungsableitung werden eine partiell differenzierbare Funktion für das Skalarfeld Φ und die Koordinaten des Ausgangspunkts P sowie die Koordinaten des Richtungsvektors benötigt. Man geht schrittweise vor und bestimmt mit den partiellen Ableitungen den Gradienten der Funktion. Im nächsten Schritt wird der Richtungsvektor durch seine Länge dividiert und somit normiert. Die Richtungsableitung ist das Skalarprodukt des Gradienten der Funktion im Punkt P mit dem normierten Richtungsvektor.
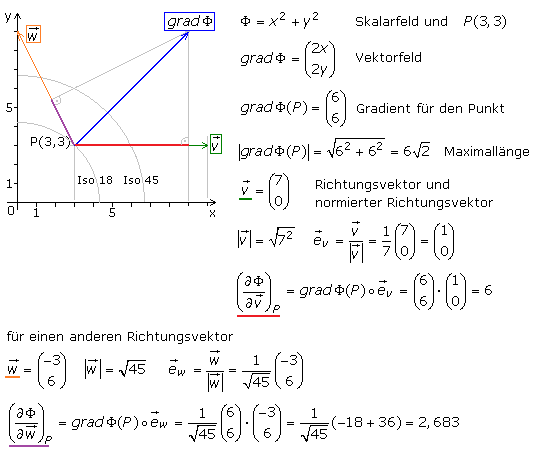
Für verschiedene Richtungen ergeben sich unterschiedliche Ergebnisse. Die Änderungsrate hat ihren Maximalwert, wenn der Richtungsvektor und damit sein Einheitsvektor mit dem Einheitsvektor des Gradienten parallel liegt. Die Richtungsableitung ist die Projektion des Gradienten der Funktion auf die vom Richtungsvektor gegebene Gerade. Die Richtungsableitung ist eine skalare Größe. Das Bild zeigt einen Ausschnitt des Skalarfelds mit der Funktion Φ in 2-D mit zwei Isolinien, wo von einem gegebenen Punkt P ausgehend die Richtungsableitungen in unterschiedliche Richtungen v und w bestimmt werden. Die Maximallänge wird nicht erreicht, da die Richtungsvektoren ungleich dem Einheitsvektor des Gradienten sind.
Divergenz
Wird der Differenzialoperator Nabla skalar mit einem Vektorfeld multipliziert, so ist das Ergebnis ein Skalarfeld. Diese Methode wird Divergenz genannt und ist ein Maß für das Auseinanderstreben (divergieren) der Vektoren in einem kleinen (infinitesimalen) Bereich. Stellt man sich das Vektorfeld als Strömungsfeld oder Flussdichtefeld vor, dann erlaubt die Divergenz eine Aussage über Quellen, von denen Vektoren ausgehen und Senken, zu denen Vektoren hinführen. Die Vektoren zeigen in die Flussrichtung und ihre Länge steht für die Menge, die den betrachteten Bereich durchfließt. Ist das Ergebnis der Divergenz positiv, so nimmt der Fluss zu und es befindet sich eine Quelle im betrachteten Bereich. Bei negativer Divergenz und abnehmenden Fluss gibt es im Bereich eine Senke. Ist das Ergebnis der Divergenz null, so ist der Bereich frei von Quellen und Senken oder der Energiefluss ist konstant mit gleichgroßem Zu- und Abfluss. Die Vektorkomponenten in den Achsenrichtungen sind selbst von den Achsenkoordinaten abhängig. Die Divergenz eines 3-D Vektorfeldes ist wie folgt definiert:
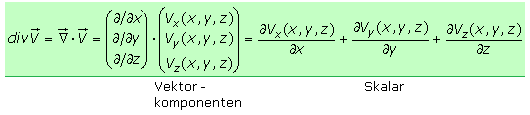
Ein Quader infinitesimaler Kantenlängen soll sich in einem 3-D Vektorfeld mit den Komponenten V(x, y, z) befinden. Betrachtet wird ein von der linken Fläche ausgehender Vektor V1 aus dem Vektorfeld, der für den Fluss durch diese Fläche steht. Ein Vektor V2, der nur in seiner x-Komponente zur rechten Fläche verschoben ist, steht dort für den Fluss durch das gleich große Flächenelement. Die Flächennormale dA ist mit dem Einheitsvektor in Achsenrichtung verbunden, steht senkrecht auf der Fläche, zeigt nach außen und der Betrag des Vektors entspricht der Flächengröße. Der Fluss durch eine Oberfläche, hier die linke und rechte, errechnet sich mithilfe der Skalarmultiplikation der Vektoren.
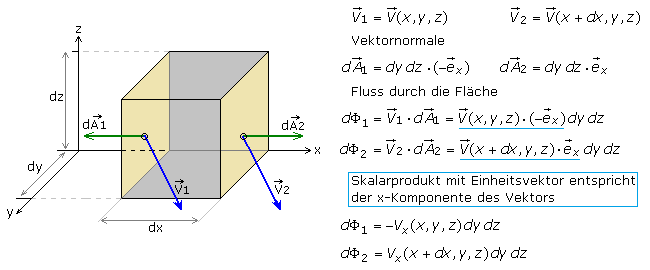
Da die Flächennormale nach Außen weist, hat sie links ein negatives und rechts ein positives Vorzeichen. Die Teilflüsse dΦ1,2 werden zum Gesamtfluss dΦ addiert. In diesem Beispiel ändert sich nur die x-Komponente um einen kleinen Betrag, während die Fläche konstant bleibt. Im folgenden Klammerausdruck steht daher die Ableitung der Funktion für die x-Komponente nach x mit der Schrittweite dx.

Summiert man über die gesamte Oberfläche des Quaders, bildet also das Integral über O, der geschlossenen Oberfläche, erhält man den Gesamtfluss durch den Quader mit dem Volumen V. Für die Flussrichtung, die senkrecht auf eine Fläche trifft und auf der Gegenseite senkrecht herauskommt, sind die Komponenten in den anderen Achsenrichtungen null, da das Skalarprodukt senkrecht aufeinander stehender Vektoren null ergibt. Die oben beschriebene Herleitung für infinitesimale Änderungen in x-Richtung kann entsprechend für die anderen Achsenrichtungen erfolgen.

Für einen Punkt im Vektorfeld ist der Fluss mithilfe der Divergenz bestimmbar. Die Summe aller Divergenzen und damit die Summe aller Quellen und Senken in einem betrachteten Volumen ist gleich dem Fluss durch die Oberfläche des Volumens. Die Divergenz ist der Fluss durch ein infinitesimal kleines Volumen oder Flächenelement, das einem Punkt entspricht. Die Divergenz eines 3-D Vektorfelds wird auch als Quellendichte pro Volumeneinheit bezeichnet.
Ein Volumen oder eine Fläche endlicher Größe kann in viele kleine aneinandergrenzende Bereiche aufgeteilt werden. An allen inneren Grenzflächen heben sich die benachbarten Flüsse wegen der entgegen gerichteten Flächennormalen auf. Der Gaußsche Integralsatz gilt auch dann für den Raum. Das Oberflächenintegral eines 3-D Vektorfelds ist über eine geschlossene Fläche gleich dem Volumenintegral aus der Divergenz des Vektorfelds, wobei die Fläche das Volumen umschließt.
Rotation – Wirbel
Die Rotation ist definiert als das vektorielle Kreuzprodukt des Differenzialoperators ∇ mit einem Vektorfeld F. Bei der Rotation handelt es sich nicht um eine Drehung im herkömmlichen Sinn, eine bessere Bezeichnung wäre Wirbel, im englischen Sprachgebrauch curl. Das Ergebnis rot F = ∇ x F ist ein neues Vektorfeld und steht für die Wirbeldichte von F. Für das kartesische Koordinatensystem errechnet sich die Rotation mit den skalaren Vektorkomponenten wie folgt:
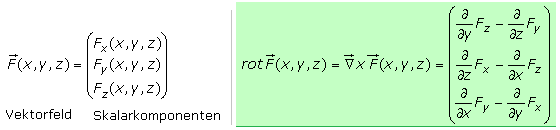
Für ein ebenes 2-D Vektorfeld ohne z-Komponente bleibt für die Rotation nur der Ausdruck der dritten Zeile stehen. Bewegt sich ein Teilchen durch ein ebenes Kräftefeld, so wird entlang eines geschlossenen Wegs Arbeit am Teilchen verrichtet. Mit der Rotation erhält man eine Aussage, ob das Vektorfeld an einem Punkt Wirbel bildet und das Teilchen auf diesem Weg verwirbelt. Bei einem positiven Ergebnis wirbelt das Feld in der Wegrichtung. Bei negativem Ergebnis ist der Weg den Feldvektoren entgegen gerichtet. Ist das Ergebnis der Rotation null, so gilt das Feld als wirbelfrei.
Die Arbeit, das Produkt aus Kraft und Weg, die am angenommenen Teilchen verrichtet wird, setzt sich additiv aus vielen kleinen Wegelementen zum geschlossenen Gesamtweg (Kontur) zusammen. Die einfachste Vorstellung für einen Weg ist der Umlauf um ein infinitesimal kleines Quadrat. Jede größere Fläche setzt sich aus vielen dieser kleinen inneren Quadrate zusammen, die alle im gleichen Umlaufsinn durchlaufen werden. Im oberen Bildteil sind es 4 gleiche kleine Quadrate, an deren gemeinsamen Innenkanten sich die Kräfte gegenseitig aufheben. Es bleibt die Wirkung entlang der äußeren Kontur. Der Gesamtumlauf um ein infinitesimal kleines Quadrat errechnet sich aus der Summe der vier Teilintegrale für jede einzelne Wegstrecke.
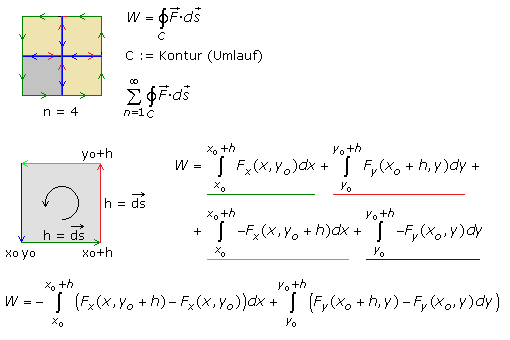
Der Umlauf beginnt links unten an P(xo, yo). Die Wegstrecke ds entspricht der Höhe des Quadrats. Auf dem Weg nach rechts ändert sich nur die x-Komponente um dx, wobei yo konstant bleibt. Es ist von xo bis (xo + h) zu integrieren. An der rechten Kante bleibt die x-Koordinate mit (xo + h) konstant und y ändert sich um dy, wobei von yo bis (yo + h) zu integrieren ist. Auf der konstanten Höhe (yo + h) führt der Weg um dx nach links zurück zur xo Ausgangsposition. Die Kraftkomponente entspricht mit negativem Vorzeichen genau der auf der unteren Wegänderung. Der Umlauf wird mit der entsprechenden negativen Kraftkomponente des rechten Wegstücks geschlossen. Die Teilintegrale lassen sich paarweise zusammenfassen.
Würde man die Klammerausdrücke der Integrale durch h dividieren, dann käme man zu einem Differenzenquotienten. Je kleiner das Quadrat und damit h wird, desto mehr nähert man sich der Ableitung des Kraftfelds nach x oder y. In den beiden Teilintegralen ändert sich entweder die x-Komponente oder die y-Komponente. Die rechte Seite der Kraftbilanz des Gesamtumlaufs entspricht der dritten Vektorkomponente der Rotation des 3-D Vektorfelds. Es ist das Ergebnis der Rotation des ebenen Vektorfelds.
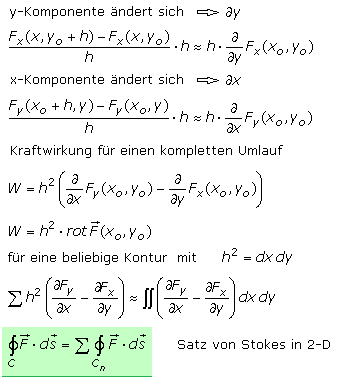
Für die Divergenz wurde der Gaußsche Integralsatz erwähnt. Für die Rotation gibt es einen entsprechenden Integralsatz nach Stokes. Mit ihm gelingt die Umwandlung eines Oberflächenintegrals in ein Kurven- oder Linienintegral. Das Vektorfeld muss stetig differenzierbar sein und die Kontur der Fläche ist so orientiert, dass die Fläche beim Durchlauf für jeden Punkt links liegt. Das Kurven- oder Linienintegral eines räumlichen Vektorfelds F entlang einer geschlossenen Kontur ist gleich dem Oberflächenintegral der Rotation von F über eine beliebige Fläche, die von der Kontur umrandet wird. Das Oberflächenintegral wird als Wirbelfluss bezeichnet, der durch eine geschlossene Fläche null ist. Für alle Flächen, die von der gleichen Kurve umrandet sind, ist der Wirbelfluss gleich groß.
In 3-D ist das Ergebnis der Rotation angewendet auf ein Vektorfeld nicht nur eine Zahl, sondern ein neues Vektorfeld. Für einen bestimmten Ort zeigt der Vektor in die Richtung, um die eine Verwirbelung stattfindet. Das folgende Bild zeigt für 2-D Vektorfelder mögliche Verwirbelungen um die z-Achse.

Für das letzte Vektorfeld ist die Rotation null und das Vektorfeld ist wirbelfrei. Ein wirbelfreies Vektorfeld ist immer als Gradient eines Skalarfelds darstellbar. Ebenso gilt die Umkehrung, dass ein Gradientenfeld wirbelfrei ist. Dagegen ist ein Wirbelfeld stets quellenfrei oder in der Umkehrung ist die Divergenz einer Rotation dann immer null.
