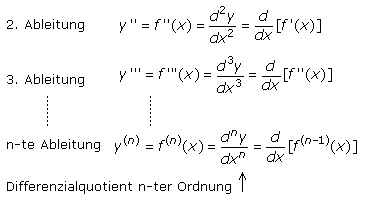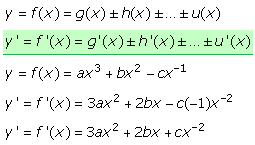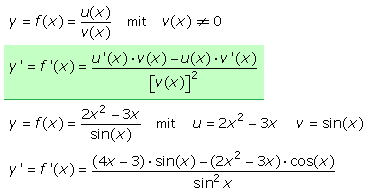Differenzialrechnung

Die Differenzialrechnung (die ebenfalls gültige Schreibweise Differentialrechnung) ist ein Werkzeug zur Bestimmung vieler Eigenschaften mathematischer Funktionen und ihren grafischen Darstellungen. Wichtige Eigenschaften sind die Steigung und das Steigungsverhalten, Extremalpunkte, Wende- und Sattelpunkte, der Krümmungsverlauf und das Monotonieverhalten. Im Mathematikunterricht wird in diesem Zusammenhang auch die Bestimmung von Nullstellen, der Schnittpunkt mit der y-Achse sowie die Punkt- und Achsensymmetrie behandelt. Diese letzten Punkte kommen ohne Differenzialrechnung aus, sind aber Teil der späteren Kurvendiskussion.

Der Funktionsbegriff

Der Funktionsgraph kann die Achsen eines ebenen rechtwinkligen Achsensystems schneiden oder berühren. In der Mathematik wird die vertikale Achse meistens als y-Achse und die horizontale Achse als x-Achse bezeichnet. Andere Problemstellungen nutzen ihre eigenen Achsenbezeichnungen, wie beispielsweise Weg-Zeit-Diagramme oder Strom-Spannungs-Diagramme. Die horizontale Achse bestimmt den Definitionsbereich der Funktion und wird auch als Abszissenachse bezeichnet. Die vertikale Achse ist die Ordinatenachse mit dem Wertebereich der Funktion. Ein gewählter Koordinatenwert auf der Abszisse (Abschnitt) bestimmt den zugehörigen Wert im Ordinatenbereich (Zuordnung). Eine beliebige Funktionsgleichung kann daher als y = f(x) geschrieben werden, mit der Aussage, dass y eine Funktion von x ist.

Nicht jede grafische (graphische) Darstellung im ebenen Achsenkreuz kann durch eine Funktionsgleichung beschrieben werden. In der Mathematik ist die Funktion einer Variablen die Vorschrift, die jedem Element x aus dem Definitionsbereich D (x ∈ D) genau ein Element y aus dem Wertebereich W (y ∈ W) zuordnet. Die unabhängige und veränderliche Variable ist x. Die davon abhängige veränderliche Variable ist y als Funktionswert. Im Folgenden sollen nur reelle Werte betrachtet werden. Die Abbilder von Kreis, Ellipse oder Spirale können somit nicht durch eine Funktion beschrieben werden.

Nullstellen

Schneidet oder berührt der Funktionsgraph die x-Achse, dann ist der Funktionswert y = 0. Es liegt eine Nullstelle oder ein Berührpunkt (Doppelnullstelle) vor. Bei bekannter Funktionsgleichung wird zur Bestimmung der Nullstelle(n) der Funktionswert f(x) = 0 gesetzt. Damit wird die Funktionsgleichung zur Bestimmungsgleichung für die x-Koordinate(n). Am leichtesten geht das bei Geraden- und Parabelfunktionen. Für Funktionen höherer Ordnung ist der Rechenaufwand entsprechend größer.

y-Achsenabschnitt

Schneidet der Funktionsgraph die y-Achse, dann ist immer der x-Koordinate des Schnittpunkts null. Hat die gegebene Funktion ein von x unabhängiges lineares Glied, so bestimmt sein Wert den y-Achsenabschnitt.

Symmetrien

Im schulischen Bereich wird nur die Achsen- und Punktsymmetrie betrachtet. Ist eine Funktion spiegelsymmetrisch zur y-Achse, dann dürfen nur geradzahlige Exponenten der unabhängigen Variablen x in der Funktionsgleichung vorkommen. Für alle x gilt dann x ∈ D ⇔ −x ∈ D. Der mathematische Nachweis muss die Gleichung f(−x) = f(x) erfüllen.

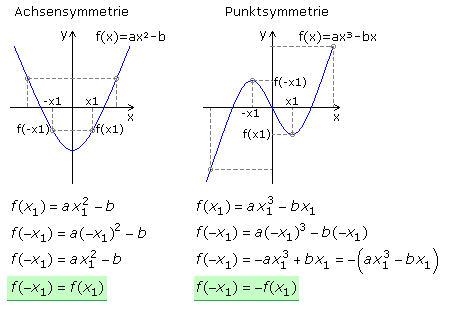
Kommen in der Funktionsgleichung nur ungeradzahlige Exponenten der x-Variablen vor, dann besteht Punktsymmetrie zum Koordinatenursprung. Die Funktionsgleichung darf kein absolutes Glied haben, denn dieses hätte mit x^o einen geraden Exponenten. Für alle x gilt dann x ∈ D ⇔ −x ∈ D. Der mathematische Nachweis muss die Gleichung f(−x) = −f(x) erfüllen.

Monotonie

Der Funktionsverlauf kann bei positiver Steigung monoton wachsend oder bei negativer Steigung monoton fallend sein. Da im Funktionsverlauf die Steigung auch gleich bleiben kann, wird das Verhalten der Monotonie durch den Zusatz streng noch genauer spezifiziert. Für alle x-Werte des Definitionsbereichs mit x1 < x2 ist die Funktion monoton wachsend, wenn f(x1) ≤ f(x2) gilt. Bei einer streng monoton wachsenden Funktion gilt f(x1) < f(x2). Bei einer monoton fallenden Funktion ist f(x1) ≥ f(x2) erfüllt und für streng monoton fallend muss f(x1) > f(x2) sein. Das Monotonieverhalten kann für die gesamte Funktion gelten oder wird für einzelne Funktionsabschnitte bestimmt.

Vom Differenzen- zum Differenzialquotient

Der Funktionsgraph einer Geraden, ein Polynom 1. Grades, hat für jeden gewählten Abschnitt des Graphen eine konstante Steigung. Wie im Kapitel über Die Gerade gezeigt wird, kann die Steigung aus dem Differenzenquotienten Δy / Δx ermittelt werden. Funktionen höherer Ordnung haben in jedem Punkt ihres Funktionsbilds fast immer unterschiedliche Steigungswerte. Die Steigung für einen bestimmten Kurvenpunkt kann durch das Anlegen und Zeichnen einer Tangente bestimmt werden. Die Tangentensteigung lässt sich dann wieder durch ihren Differenzenquotienten ermitteln.

Diese grafisch weniger genaue Bestimmungsmethode wird durch die Differenzialrechnung zu einer allgemeingültigen optimalen Methode. Mit ihr lassen sich Steigungen für jeden Kurvenpunkt direkt bestimmen, wenn die gegebene Funktion differenzierbar ist. Die Gerade, die durch zwei nahe beieinanderliegende Kurvenpunkte geht, heißt Sekante. Ihre Steigung ist aus dem Differenzenquotienten unter Verwendung der beiden Kurvenpunktkoordinaten bestimmbar. Wandert ein Punkt P entlang des Funktionsgraphen auf einen feststehenden Kurvenpunkt P1 zu, so geht die Sekante beim Erreichen von P1 in die Tangente über.

Die Tangente im Kurvenpunkt P1 wird als Grenzlage verstanden. Die Sekanten durch den festen Punkt P1 und einem weiteren Kurvenpunkt P, der sich P1 nähert, verändern ihre Steigung. Fallen beide Punkte zusammen, dann sind Sekanten- und Tangentensteigung in P1 als Grenzwert gleich. Im folgenden Videoclip wird dieser Übergang nacheinander für vier Kurvenpunkte schrittweise dargestellt. Eine individuelle Steuerung ist nur mithilfe der einblendbaren Controlleiste möglich.

Es ist vorstellbar, dass sich zu einem ausgewählten Kurvenpunkt P1 Sekanten zeichnen lassen, deren zweiter Kurvenpunkt rechts oder links von P1 liegt. Die Steigungen der Sekanten stehen für einen Mittelwert zum gesuchten Momentanwert der Steigung für die Tangente für P1. Ergeben beide Steigungsfolgen der Sekanten von rechts und links kommend beim Grenzübergang, wo der Differenzenquotient in den Differenzialquotienten übergeht, den gleichen Grenzwert, so ist die betrachtete Funktion an der Stelle P1 differenzierbar.

Die Funktion f(x) ist im Definitionsbereich stetig. Sie ist an jeder Stelle differenzierbar, wenn für jeden Kurvenpunkt der rechts- und linksseitige Grenzwert gleich der Tangentensteigung in diesem Kurvenpunkt ist. Für f(x) existiert eine Ableitungsfunktion f ' (x), die den Wert der Steigung für jeden Kurvenpunkt bestimmt.

Grenzwertbestimmung

Die folgende Darstellung zeigt den Ausschnitt eines Funktionsgraphen. Die Tangentensteigung im Punkt P(xo/yo) wird durch den Übergang vom Differenzen- zum Differenzialquotienten bestimmt. Dazu ist oberhalb von P ein weiterer Punkt Q eingezeichnet, der um den x-Achsenabschnitt Δx entfernt liegt. Mit diesem Wert errechnet sich der Funktionswert zu f(xo + Δx). An der Stelle P ist der Funktionswert f(xo). Durch die Punkte P und Q verläuft die Sekante mit der Steigung Δy/Δx, die sich aus dem Steigungsdreieck ergibt. Nähert sich der Punkt Q dem Punkt P, so wird das mathematisch mithilfe der Grenzwertbildung durch den Limes, wo Δx gegen null strebt, beschrieben.

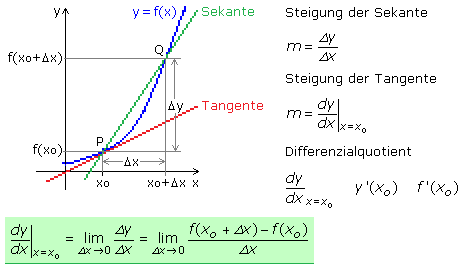
Das folgende Beispiel zeigt die Anwendung der Grenzwertbildung für die Funktionsgleichung einer Geraden. Ihre Steigung ist in allen Kurvenpunkten konstant und entspricht somit auch dem Differenzenquotienten. Im Term des Differenzialquotienten kürzt sich Δx heraus, sodass die Grenzwertbildung nicht mehr notwendig wird.

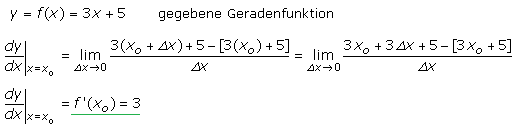
Der Rechenweg gilt auch für Funktionen höherer Ordnung. Das folgende Beispiel zeigt die Grenzwertbildung für eine Parabelfunktion, ein Polynom 2. Grades.

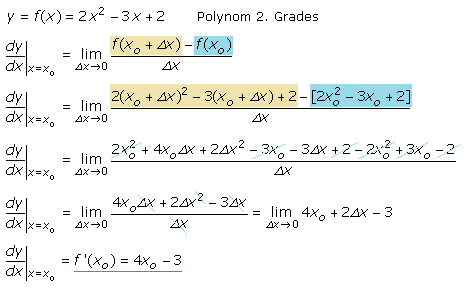
Im Videoclip ist der im 1. Quadranten verlaufende Ast der Hyperbel mit der Funktionsgleichung f(x) = 10/x dargestellt. Die Ableitfunktion für diese Stammfunktion kann ebenso ermittelt werden wie in den vorangegangenen Beispielen. Ein Vergleich mit den im Video ermittelten Tangentensteigungen und den mit der folgenden Ableitgleichung errechenbaren Werten für den ausgewählten Punkt zeigt die Richtigkeit des Verfahrens.

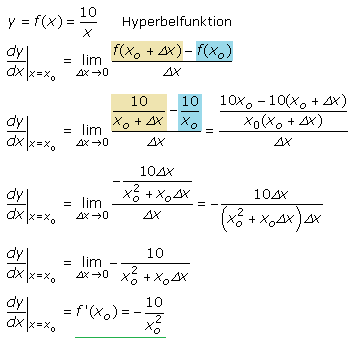
Die Steigungsfunktion mithilfe der Grenzwertbildung zu berechnen ist umständlich, da beim Vergleich der gegebenen Polynomfunktion mit der Ableitfunktion eine Bildungsregel zu erkennen ist. Sie gilt auch für echt-gebrochen-rationale Funktionen in deren Zählern keine Potenzen größer x^o = 1 vorkommen. Um die Tangentensteigungs- oder Ableitfunktion zu bilden, wird bei der gegebenen Funktion der Exponent der Variablen des betrachteten Glieds als Faktor vor das Glied gesetzt und der Exponent um 1 erniedrigt. Da jede Konstante formal mit x^o multipliziert geschrieben werden kann, ist das Ergebnis ihrer Ableitung gleich 0.

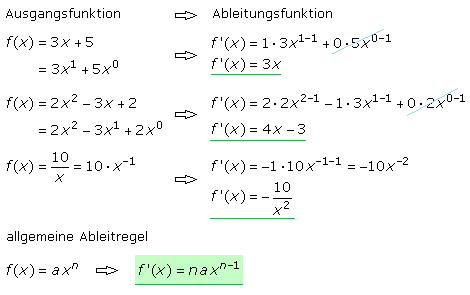
Mit der Ableitungsfunktion kann an jeder Stelle x aus dem Definitionsbereich eines differenzierbaren Funktionsintervalls der Wert der Steigung der Tangente für den Funktionswert ermittelt werden. Die 1. Ableitung angewendet auf eine Ausgangsfunktion ergibt als neue Funktion deren Steigungsfunktion. Der Differenzialoperator d/dx angewendet auf f(x) führt zur Steigungsfunktion. In der Physik wird die Geschwindigkeit als Änderung des Ortes nach der Zeit bestimmt, somit nach t abgeleitet. Die abgeleitete Größe wird meistens mit einem darüberstehenden Punkt und nicht wie in der Mathematik mit einem ' (Hochkomma) geschrieben.

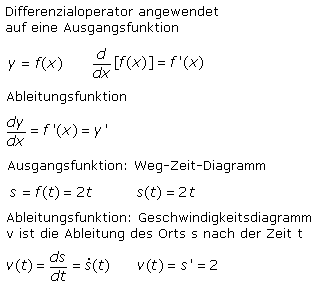
Höhere Ableitungen

Hat die 1. Ableitung noch Potenzen von x größer null, so kann der Differenzialoperator erneut angewendet werden. Das Ergebnis ist die 2. Ableitung und somit die Steigungsfunktion der 1. Ableitung. Dieser Prozess kann wiederholt werden, solange in der höheren Ableitung die abzuleitende Variable noch enthalten ist. Durch mehrfaches Ableiten lassen sich die Eigenschaften von Funktionen höheren Grades eindeutig beschreiben.

Ableitungsregeln

Faktor- und Potenzregel

Bei Differenzieren bleibt der konstante Faktor einer Variablen unverändert erhalten. Ein von der Variablen unabhängiger konstanter Wert wird beim Differenzieren zu null. Der Exponent der Variablen wird als Faktor vor die Variable geschrieben und der neue Exponent wird um 1 erniedrigt.

Summen- und Differenzregel

Ist die gegebene Funktion eine endliche Summe oder Differenz von Teilfunktionen, so wird jedes Glied nach der Faktor- und Potenzregel einzeln differenziert. Diese Methode findet ihre Anwendung bei Polynomfunktionen. Sie können als Linearkombination einzelner Funktionen mit der gleichen Variablen verstanden werden.

Produktregel

Diese Regel ist anzuwenden, wenn zwei Funktionen miteinander multipliziert werden. Ein fast selbsterklärendes Beispiel ist die Multiplikation zweier unterschiedlicher Potenzen für dieselbe Variable x. Hier kann vor der Ableitung das Potenzgesetz angewendet werden, indem die Exponenten addiert werden. Die Ergebnisfunktion kann dann einfach nach der Potenzregel abgeleitet werden. Das zweite Beispiel zeigt die Multiplikation von zwei nicht zusammenfassbaren Teilfunktionen.

Quotientenregel

Die Quotientenregel ist anzuwenden, wenn eine gebrochen rationale Funktion abgeleitet werden soll, wo die Variable im Zähler und Nenner in nicht zusammenfassbaren Teilfunktionen vorkommt.

Kettenregel

Die gegebene Funktion ist nicht elementar differenzierbar und stellt die Funktion einer anderen Funktion dar. Es handelt sich um miteinander verkettete Funktionen y = f(x) = F(u(x)). Die gegebene Ausgangsfunktion wird durch eine Substitution u = u(x) in eine von u abhängige elementare Funktion y = F(u) umgewandelt. Die Substitution u(x) wird als innere Funktion und die damit gebildete Funktion F(u) als äußere Funktion bezeichnet. Beide Funktionen müssen nach ihrer unabhängigen Variablen differenzierbar sein. Die gesuchte Ableitfunktion ist die Multiplikation der äußeren und inneren Ableitung und anschließender Rücksubstitution von u. Das scheint kompliziert zu sein, ist am Beispiel aber leicht nachvollziehbar.

Die Kettenregel kann auch auf mehrfach verkettete Ausgangsfunktionen angewendet werden. Im folgenden Beispiel muss eine zweimalige Substitution durchgeführt werden, um elementar differenzierbare Teilfunktionen zu erhalten. Vorangestellt ist das allgemeine Lösungsverfahren.

Ableiten von e-Funktionen

Bei der einfachsten e-Funktion y = f(x) = e^x ist die Variable der Exponent zur Basis e = 2,71828..., der Eulerschen Zahl. Diese Exponentialfunktion ist eine elementare Funktion, deren erste Ableitung ebenso lautet. Ist der Exponent eine Funktion von x, dann erfolgt die Ableitung nach der Kettenregel oder einfacher gesagt, die e-Funktion bleibt erhalten und wird mit der Ableitung des Exponenten multipliziert. Ist die e-Funktion mit einer anderen Funktion der gleichen Variablen (im Beispiel t) multipliziert, dann ist beim Ableiten zusätzlich die Produktregel anzuwenden.

Ableiten von ln-Funktionen

Die einfachste elementare Funktion des natürlichen Logarithmus y = f(x) = ln(x) hat als erste Ableitung y' = 1/x. Hat die Logarithmusfunktion eine andere Basis, so wird noch durch den natürlichen Logarithmus der Basis dividiert. Ist der Klammerausdruck eine Funktion der Variablen, so muss wie bei der e-Funktion noch mit der inneren Ableitung der Funktion multipliziert werden. Die Ableitung erfolgt somit nach der Kettenregel.