Analytische Geometrie – Vektorgeometrie
Mit der Kenntnis über die Eigenschaften und den prinzipiellen Rechenregeln der Vektoralgebra werden hier einige Anwendungen beschrieben, bei denen Vektoren nützlich sein können. Die analytische Geometrie befasst sich mit Punkten, Geraden, Ebenen und anderen geometrischen Formen. Das Ziel ist es, die Beziehungen zwischen den geometrischen Darstellungen mathematisch zu beschreiben. Oft setzt das individuelle Vorstellungsvermögen Grenzen, um geometrisch Probleme in räumlicher Darstellung zu lösen. Mit mathematisch algebraischen Verfahren wird es einfacher. Analytische Geometrie und Vektorgeometrie ergänzen sich und setzen ein Koordinatensystem voraus. Das Bezugssystem sollen hier nur rechtwinklige Koordinatensysteme der Ebene und des Raumes mit ihrem Koordinatenursprungspunkt sein.
Vektorielle Darstellung von Geraden
Ist in einem Bezugssystem die Lage eines Startpunktes und davon ausgehend die Richtung bekannt, so kann eine eindeutige Gerade gezeichnet werden. Ebenso ist die direkte, kürzeste Verbindung zwischen zwei gegebenen Punkten eine Gerade. Mit zwei Koordinatenangaben kann die Bestimmungsgleichung einer Geraden aufgestellt werden. Das im ebenen Koordinatensystem angewendete Verfahren kann auf das räumliche Koordinatensystem erweitert werden.
Im weiteren Fließtext werden Vektoren durch hervorgehobene Buchstaben ohne Pfeil geschrieben.
Punkt-Richtungs-Form
Die Lage des Punkts P (Stützpunkt) ist durch den Ortsvektor r1 bestimmt, der im Koordinatenursprung beginnt und bei den Punktkoordinaten endet. Von dort zählen die Koordinaten des Richtungsvektors a, der kein Nullvektor sein darf. Bei einer Ursprungsgeraden ist der Ortsvektor ein Nullvektor und die Parameterform der Geradengleichung wird nur durch den Richtungsvektor bestimmt. Wird er mit einem skalaren (reellen) Parameter λ multipliziert, so sind mithilfe der Parameterdarstellung alle Punkte der Geraden bestimmbar. In der Skizze steht auch die oft mit Spaltenvektoren geschriebene vektorielle Geradendefinition.

Eine Gerade im Raum ist entsprechend durch einen Stützpunkt, seinem Ortsvektor und einen Richtungsvektor definiert. Orts- und Richtungsvektor haben als Spaltenvektoren geschrieben dann drei Komponenten.
Zweipunkteform
Sind die Koordinaten zweier unterschiedlicher Punkte einer Geraden gegeben, kann die vektorielle Geradengleichung nach dem gleichen Grundprinzip erstellt werden. Ist P1 der Stützpunkt und P2 ein weiterer Geradenpunkt, so ergibt sich der Richtungsvektor aus dem Vektor P1P2 und errechnet sich aus der Differenz der Komponenten von P2 − P1.
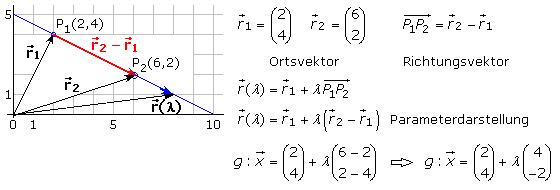
Die vektorielle Darstellung für Geraden im rechtwinklig räumlichen Koordinatensystem in Parameterschreibweise erfolgt nach dem gleichen Bildungsprinzip mit Ortsvektor und Richtungsvektor, wobei der Richtungsvektor kein Nullvektor sein darf. Sind die Komponenten des Richtungsvektors gegeben, werden sie anstelle der Differenz direkt eingesetzt.
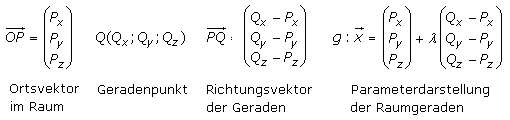
Die Parameterschreibweise ist die spezielle Darstellung einer Geraden. Sie unterscheidet sich von der aus der Analysis algebraischen Geradengleichung mit Steigung und Achsenabschnitt. Für jede definierte Gerade müssen beide Darstellungen gleichwertig und umwandelbar sein. In der Analysis werden die Koordinatenachsen mit x, y und z bezeichnet, wo in der analytischen Geometrie oft x1, x2 und x3 geschrieben steht. Zur einfacheren Vorstellung bleibe ich in den Beispielen bei Geraden in der Ebene mit x und y Koordinaten.
Parameterform in Koordinatenform
Das folgende Rechenbeispiel verwendet die Parameterform der oben dargestellten Geraden. Sie kann in die Koordinatenform und weiter in die gewohnte Geradenfunktion mit Steigung und Achsenabschnitt umgewandelt werden. Dazu wird ein lineares Gleichungssystem (LGS) aufgestellt, wobei die in Spaltenvektoren geschriebene Parameterform zeilenweise ausgelesen wird. Der Parameter λ kommt in beiden Gleichungen vor und kann mit λ = 1 eliminiert werden. Aus der Koordinatenform Gerade kann durch einfache Umstellung die Funktionsgleichung y = f(x) geschrieben werden.

Parameterform in Normalenform
Die Parameterform einer Geraden in der Ebene kann leicht in die Normalenform umgewandelt werden. Im ersten Ausdruck der Parameterform stehen die Koordinaten des Ortsvektors gefolgt von denen des Richtungsvektors. Der Normalenvektor n steht senkrecht auf dem Richtungsvektor a und wird einfach durch Vertauschen der Spaltenkomponenten erhalten, wobei eine Komponente zusätzlich negiert wird. Dieser Ansatz muss auch für jeden weiteren Punkt auf der Geraden mit den Koordinaten P(x;y) gelten. Ein bekannter Punkt ist der Endpunkt P des Ortsvektors, der andere Punkt erhält mit x und y die allgemeinen Koordinaten. Wird das Skalarprodukt der Normalenform aufgelöst, so folgt nach Umstellung die Funktionsgleichung y = f(x).

Orthogonale Vektoren
Ist das Skalarprodukt von Vektoren in der Ebene oder im Raum null, dann sind die Vektoren senkrecht (orthogonal) mit einem 90° Winkel zueinander ausgerichtet. Ist das Ergebnis des Skalarprodukts der Richtungsvektoren von Geraden gleich null, so verlaufen diese Geraden rechtwinklig zueinander.
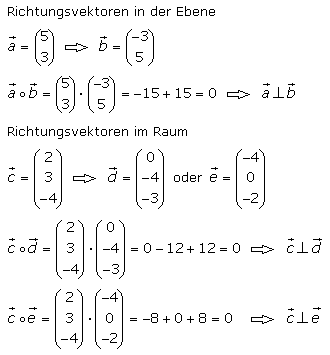
Soll ein Vektor bestimmt werden, der senkrecht zu einem gegebenen Vektor verläuft, dann werden die Komponenten der Spaltenschreibweise des gegebenen Vektors vertauscht und eine Komponente negiert. Für Vektoren im Raum wird eine beliebige Komponente null gesetzt, die anderen beiden werden getauscht und bei einer wird das Vorzeichen gewechselt.
Das Ergebnis des Vektor- oder Kreuzprodukts ergibt einen Vektor, der senkrecht auf seinen beiden Ausgangsvektoren steht. Das Skalarprodukt des Ergebnisvektors mit jedem der Ausgangsvektoren muss folglich null ergeben.
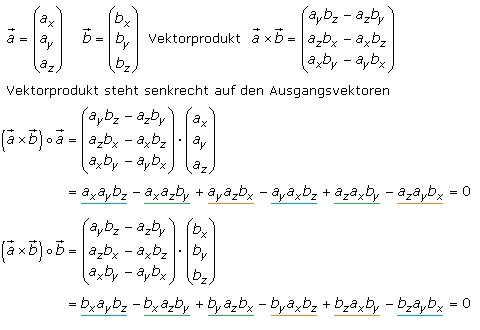
Lineare Abhängigkeit
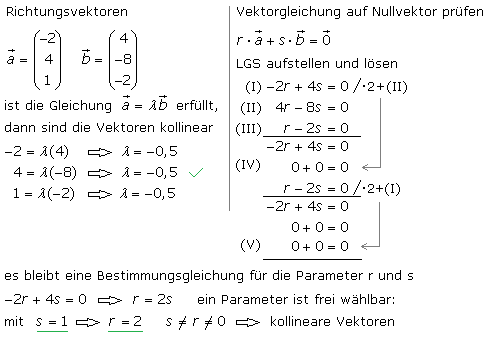
Vektoren sind linear abhängig, wenn sie parallel verlaufen. Zueinander sind es Vielfache unterschiedlicher Länge. Die Prüfung auf lineare Abhängigkeit in der Ebene und im Raum findet mithilfe der Richtungsvektoren statt. Beim Vergleich der Spaltenkomponenten von zwei Vektoren muss sich ein konstanter Parameter ergeben. Verlaufen die Vektoren parallel aber in Gegenrichtung im Winkel von 180°, so ist ihr Verhalten ebenfalls kollinear und sie sind linear abhängig. Wird mit den Richtungsvektoren und unterschiedlichen Parametern die Vektorgleichung aufgestellt, so ist für kollineare Vektoren das Ergebnis der Nullvektor. Dabei dürfen nicht alle Parameter null sein. Die Berechnung kann nach dem Aufstellen des linearen Gleichungssystems (LGS) erfolgen. Wird beim Lösungsverfahren des LGS nach Gauß eine Zeile null, dann sind die Vektoren linear abhängig.
Die lineare Abhängigkeit von drei Vektoren kann durch Berechnen der Determinante mit der Regel nach Sarrus ermittelt werden. Ist das Ergebnis null, so sind die Vektoren linear abhängig. Dieses schnellere Bestimmungsverfahren liefert keine Werte für die skalaren Streckungsfaktoren (Parametern). Das Verfahren kann auch für Geraden in der Ebene und dem Lösen der zweireihigen Determinante angewendet werden.
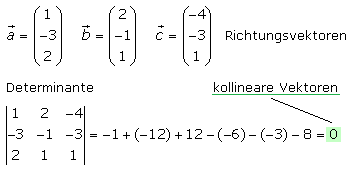
Lage von Geraden im Raum
Im Raum können Geraden in einer Ebene zueinander parallel verlaufen und auch direkt aufeinander liegen, also identisch sein. Sind sie nicht parallel, so können sie einen gemeinsamen Schnittpunkt haben oder auf verschiedenen (windschiefen) Ebenen ohne einen Schnittpunkt verlaufen. Beispiele zu windschief sind für separate Flugebenen, Kreuzungen von Straßen und Autobahnen und überbrückten Bahngleisanlagen zu finden. Zur rechnerischen Überprüfung sind die Geradengleichungen durch einen Stützpunkt mit seinem Ortsvektor und einem Richtungsvektor definiert.
Der parallele Verlauf wird mit den Richtungsvektoren nachgewiesen, wie es im vorigen Abschnitt mit dem Nachweis zur linearen Abhängigkeit beschrieben steht. Wenn sie parallel, also linear abhängig sind und keinen gemeinsamen Schnittpunkt haben, dann sind sie nicht identisch und verlaufen 'echt' parallel. Der Nachweis gelingt mit der Punktprobe und den Koordinaten des Ortsvektors. Erfüllt der Ortsvektor der einen Geraden die andere Geradengleichung, so sind beide Geraden deckungsgleich und identisch. Parallele Geraden haben keinen gemeinsamen Punkt. Die Lageüberprüfung wird mit den drei Geraden g, h und k im Raum durchgeführt.

Im folgenden Beispiel sind die Geraden nicht parallel, da ihre Richtungsvektoren keine Vielfache sind. Die Geraden können genau einen Schnittpunkt haben oder sie sind windschief zueinander und haben keinen Schnittpunkt. Für die Überprüfung wird für das Geradenpaar g und h sowie g und k das LGS aufgestellt, um die Parameter zu berechnen. Gibt es bei den Parametern einen Widerspruch, so hat das Geradenpaar keinen Schnittpunkt und die Geraden sind zueinander windschief.
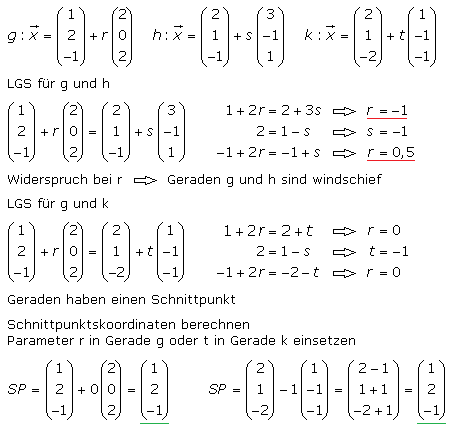
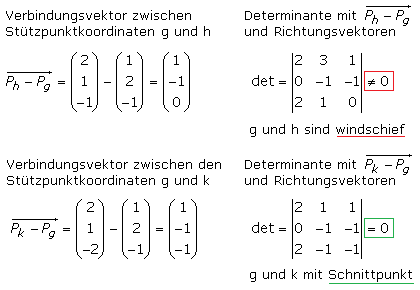
Ohne LGS kann mit dem Berechnen einer Determinante geprüft werden, ob ein Geradenpaar im Raum windschief ohne Schnittpunkt verläuft. Es wird der Verbindungsvektor zwischen den Stützpunktkoordinaten des Geradenpaars ermittelt und die Determinante mit den beiden Richtungsvektoren und dem Verbindungsvektor aufgestellt. Ist das Ergebnis ungleich null, so sind die Geraden zueinander windschief. Der Nachweis wird für die Geradenpaaren g und h sowie g und k gezeigt und stimmt mit dem Ergebnis zuvor überein.
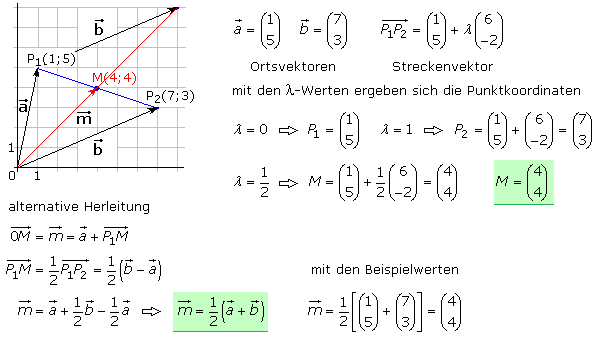
Mittelpunkt einer Strecke
Die vektorielle Bestimmung eines Streckenmittelpunkts ist in der Ebene und im Raum nach dem gleichen Verfahren möglich. Mit den Koordinaten des Streckenanfangs- und Endpunkts sind deren Ortsvektoren bekannt und der Richtungsvektor kann bestimmt werden. Da der Mittelpunkt den Richtungsvektor symmetrisch teilt, ist er mit dem Faktor 0,5 zu multiplizieren. Das Gleichungssystem der Parameterform liefert den Ortsvektor zum Mittelpunkt und somit die Mittelpunktkoordinaten. Die andere dargestellte Bestimmungsmethode kommt ohne den Zwischenschritt und dem Aufstellen der Gleichung für den Streckenvektor P1P2 aus.