Vektoralgebra
Zur genauen Beschreibung vieler physikalischer Eigenschaften reichen Betragszahlen mit ihren Maßeinheiten nicht aus. So fehlt zum Beispiel bei der Geschwindigkeit, der magnetischen oder elektrischen Feldstärke neben der Betragsangabe noch die Richtung. Strecken gleicher Länge können in der Ebene oder im Raum unterschiedliche Ausrichtungen haben. Ein Vektor ist eine gerichtete Größe und wird symbolisch durch einen Pfeil dargestellt. An ihm kann die Maßzahl und die Richtung abgelesen werden. Die Länge des Pfeils steht für die Maßzahl gleichsam dem Betrag. Die Pfeilspitze zeigt in die Richtung, wohin die Länge weist oder wirkt. Die folgenden Abschnitte bieten allgemeine und mathematische Überblicke, um sinnvoll mit Vektoren zu arbeiten.
Nach Hinweisen zu den Vektoreigenschaften folgen Abschnitte zur Komponentendarstellung, der Addition und Subtraktion, der Vektorvervielfachung, zur Ermittlung der Länge eines Vektors, zur Normierung, zum Skalarprodukt, Hinweise zur Projektion auf einen Vektor, dem Vektorprodukt und dem Spatprodukt.
Allgemeine Eigenschaften von Vektoren
Als Vektorsymbole findet man für Feldgrößen wie dem E-Feld oder B-Feld Großbuchstaben unter einem Pfeil. Einzelne symbolische Feldlinien werden als Pfeile gezeichnet, deren Pfeilspitzen in die Wirkrichtung des Feldes zeigt. Der Vektorpfeil kann mit einen Kleinbuchstaben in Frakturschrift (deutsche Schreibschrift) oder einen Kleinbuchstaben unter einem Pfeil (lateinische Schreibschrift) gekennzeichnet werden. Soll nur die Länge des Vektors berücksichtigt werden, so sollte das Vektorsymbol zwischen doppelte Betragszeichen geschrieben werden. In vielen Fällen wird nur das einfache Betragszeichen verwendet.
Eine Ebene kann mithilfe eines rechtwinkligen Achsensystems sehr gut charakterisiert werden. Ähnlich den Punktkoordinaten P(x;y) können Vektoren in der Ebene eindeutig durch Vektorkoordinaten in x- und y-Richtung, beschrieben werden. Normalerweise werden sie in runden Klammern untereinander, können im Fließtext platzsparend auch nebeneinander geschrieben werden. Jeder Vektor hat einen Anfangs- und Endpunkt. Die Differenz der Koordinaten vom Endpunkt minus Anfangspunkt ergibt die Vektorkoordinaten. Die folgende Skizze zeigt die Zusammenhänge.

Die Länge eines Vektors und keine gerichtete Größe sondern eine Zahl, eine skalare Größe. Oft gehört zum Skalar noch die Angabe der Maßeinheit. Soll die Länge berechnet werden, so müssen die einzelnen Vektorkoordinaten quadriert und aufsummiert werden. Die Länge ist dann die Wurzel aus der Summe.
Ein Vektor wird eindeutig durch die Lage seines Anfangs- und Endpunkts beschrieben. Der Punkteabstand ist seine Betragszahl. Zur physikalisch-technischen Vektorbeschreibung gehört die Maßeinheit.
Ganz allgemein ist der Vektor ein Vertreter der Menge aller Vektoren (Pfeile) mit gleicher Richtung und Länge. Diese Vektoren bilden eine Vektorklasse. Sie sind zueinander gleich, wenn sie durch Parallelverschiebung zur Deckung gebracht werden können. Sie stimmen in Betrag (Skalar) und Richtung, also allen Komponenten überein. Das Bild zeigt die Vektoren a und b als Richtungsvektor. Sie sind der jeweils einzige Vertreter ihrer eigenen Vektorklasse.
In der Skizze kann jeder der beiden Vektoren unabhängig vom anderen parallel zu sich selbst verschoben werden. Dabei verändern sich seine Eigenschaften nicht. Diese Vektoren werden als freie oder ungebundene Vektoren bezeichnet. Darf die Verschiebung nur entlang der Wirkungsrichtung erfolgen, so handelt es sich um linienflüchtige Vektoren. Werden die Vektoren parallel zu sich verschoben, dass ihre Anfangspunkte an den Ursprungspunkt des Koordinatensystems fest zu liegen kommen, dann werden sie als gebundene Vektoren bezeichnet. Immer bleiben ihre Länge und Richtung sowie ihre Vektorkoordinaten dabei gleich.
- Skalar:
- Es handelt sich um eine nicht gerichtete Größe, die durch eine reelle Zahl und Maßeinheit eindeutig beschrieben ist.
- Freier Vektor – Richtungsvektor:
- Er ist nicht an den Ursprungspunkt eines Koordinatensystems gebunden und wird auch als ungebundener Vektor bezeichnet. Er ist definiert durch seinen Betrag und seine Richtung und kann unter Beibehaltung dieser Eigenschaften parallel zu sich selbst verschoben werden. Der Richtungsvektor verbindet zwei Punkte in der Ebene oder im Raum und ist die kürzeste Verbindung zwischen zwei Ortsvektoren. Wird ein Richtungsvektor mit einem Skalar multipliziert, so bleibt seine Richtung unverändert und nur der Betrag ändert sich.
- Gebundener Vektor:
- Es ist ein durch seinen Anfangs- und Endpunkt festgelegter Vektor. Ohne Änderung der Anfangsbedingungen kann er nicht parallel verschoben werden. Von einem festen Punkt ausgehend ist er durch seinen Betrag und seine Richtung eindeutig definiert.
- Ortsvektor:
- Es ist ein an den Ursprungspunkt des Koordinatensystems (Nullpunkt) gebundener Vektor, der von dort gerichtet zum definierten Endpunkt verläuft. Er kann nicht parallel verschoben und nicht mit einem Skalar multipliziert werden.
- Nullvektor:
- Es ist ein Vektor der Länge 0 mit unbestimmter Richtung.
Parallele Vektoren müssen nur in ihrer Richtung übereinstimmen. Antiparallele Vektoren haben einen mit 180° entgegengesetzten Richtungssinn. Parallele und antiparallele Vektoren sind kollineare Vektoren. Sie dürfen durch Parallelverschiebung auf eine gemeinsame Linie gelegt werden.
Einen Vektor mit gleichem Betrag (und Maßzahl) und entgegengesetzter Richtung nennt man inversen oder Gegenvektor. Er ist zu sich selbst der antiparallele Vektor. Seine Koordinaten unterscheiden sich durch das Vorzeichen. Die Addition von Vektor und Gegenvektor ergibt einen Nullvektor. Anfangs- und Endpunkte sind identisch, sein Betrag ist 0 und er hat keinen Richtungssinn.
 △
△
Vektoren im kartesischen Koordinatensystem
Komponentendarstellung
Das numerische Rechnen mit Vektoren ist anschaulicher, wenn sie in ein Koordinatensystem eingebunden sind. Bewährt hat sich das räumliche kartesische Koordinatensystem, wo die drei Koordinatenachsen x, y und z jeweils paarweise zueinander rechte Winkel bilden. Liegen die zu berechnenden Vektoren in einer Ebene, so entfällt die z-Achse und es bleibt das ebene rechtwinklige xy-Achsensystem.
Im räumlichen Koordinatensystem werden den drei Achsen in Achsenrichtung Einheits- oder Basisvektoren zugeordnet. Sie sind als Ortsvektoren an den Koordinatenursprung gebunden, mit dem Betrag 1 stehen sie rechtwinklig (orthogonal) zueinander. Ihre Symbole sind oft als ![]() geschrieben.
geschrieben.
Hier werden im Fließtext die Vektoren durch hervorgehobene Kleinbuchstaben ohne Pfeil geschrieben.
Das Bild zeigt den Ortsvektor a im kartesischen Koordinatensystem. Er ist durch seine Vektorkoordinaten ax, ay, az bestimmt, die sich bei der jeweils senkrechten Projektion des Vektors auf die Koordinatenachsen ergeben. Werden die skalaren Koordinatenwerte mit den jeweiligen Einheitsvektoren e multipliziert, erhält man drei Ortsvektoren, die entsprechend addiert einen Richtungsvektor ergeben, der gleich dem gegebenen Ortsvektor a ist.
Eine äquivalente Darstellung ist die Summe der Einheitsvektoren multipliziert mit dem jeweiligen Skalar, der zum Erreichen des Endpunkts notwendig ist. Das entspricht dann den Vektorkomponenten. Am meisten genutzt wird die Schreibweise in Form des Spaltenvektors. Im Fließtext ist es einfacher ihn als Zeilenvektor a = (ax ay az) zu schreiben.

Wird der Vektor zu sich selbst parallel verschoben, so bleiben die Länge und die Richtung (Richtungssinn) gleich. Die Koordinaten des Vektors bleiben bei der Parallelverschiebung unverändert (invariant). Bei einem gebundenen Vektor sind die Koordinaten des Anfangs- und Endpunktes festgelegt. Für die Koordinaten- und Komponentendarstellung und die Schreibweise des Spaltenvektors verschiedener Vektoren gilt:
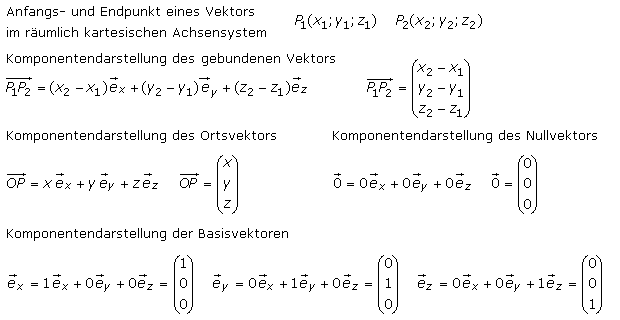 △
△
Addition und Subtraktion von Vektoren
Wirkt eine ausreichend große Kraft auf eine ruhende Masse, so bewegt sie sich um eine bestimmte Strecke in Richtung der Kraft. Wirken am selben Punkt der Masse mehrere Kräfte in verschiedene Richtungen, dann ist die Streckenlänge und die Bewegungsrichtung eine andere. Das Ergebnis kann mithilfe der Vektorrechnung ermittelt werden.
Vektoren sind gerichtete Größen, deren Eigenschaften erhalten bleiben, wenn sie parallel zu sich selbst verschoben werden. Das Bild zeigt zwei Vektoren, die in der Ebene ausgehend vom Anfangspunkt (2;5) wirken. Mithilfe der Parallelverschiebung werden die Vektoren miteinander verbunden. Es ergibt sich der resultierende Summenvektor, der vom Anfangspunkt (2;5) zum Endpunkt P(8;5) zeigt.
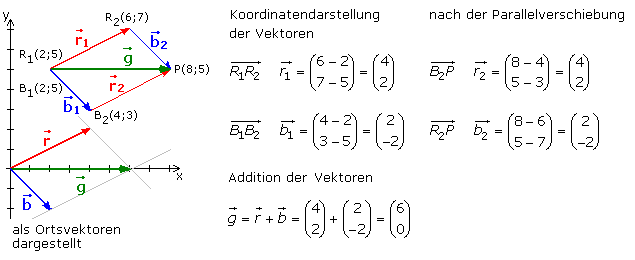
Die beiden Vektoren R1R2 und B1B2 sind für sich gesehen freie Vektoren. Sie lassen sich als Zeilenvektor r1 = (4 2) und b1 = (2 −2) oder wie im Bild als Spaltenvektor schreiben. Wird durch Parallelverschiebung der Vektor b1 mit seinem Anfangspunkt B1 an den Endpunkt R2 des Vektors r1 gesetzt, dann ändern sich seine Punktkoordinaten. Der Punkt B1 liegt auf dem Punkt R2 und ist additiv um horizontal 4 und vertikal 2 Einheiten verschoben worden. Damit die Richtung des Vektors gleich bleibt, müssen die Koordinaten von B2 ebenfalls additiv um horizontal 4 und vertikal 2 geändert werden. Der zu b1 verschobene und kollineare Vektor b2 hat die Kordinaten P(8;5) für den Endpunkt.
Das Bild zeigt, dass mit gleichem Ergebnis auch den Vektor r1 parallel zu sich entlang dem Vektor b1 verschoben werden kann. Der Endpunkt des neuen Vektors r2 ist ebenfalls P(8;5). Für den Summenvektor g gilt folglich: g = r1 + b2 = b1 + r2.
Liegen die Anfangspunkte der Vektoren im Koordinatenursprung, dann ist auch bei Ortsvektoren das Additionsergebnis identisch. Gleiches gilt für Vektoren im dreidimensionalen Koordinatensystem. Das Ergebnis der vektoriellen Addition oder Subtraktion ist ungleich der Summe oder Differenz ihrer Beträge (Längen), es sei denn, die Vektoren liegen kollinear.
Gegenvektor
Werden die Vektorkoordinaten eines Vektors mit (-1) multipliziert, also invertiert, dann entsteht der Gegenvektor. Er hat die gleiche Länge und bildet mit dem Ursprungsvektor einen Winkel von 180°, zeigt oder wirkt in die Gegenrichtung. Soll von einem Vektor a der Vektor b subtrahiert werden, dann werden seine Vektorkoordinaten von denen des Vektors a subtrahiert. Das entspricht der Addition von a und dem Gegenvektor −b.
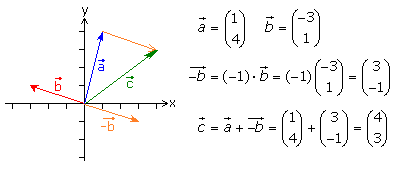
Rechenregeln der Addition und Subtraktion
Wie in der Mathematik mit Zahlen, den skalaren Größen, gilt auch bei der Addition und Subtraktion von Vektoren das Kommutativ- und Assoziativgesetz. Zur mathematischen Bestimmung des Summenvektors werden die Komponenten der einzelnen Vektoren miteinander addiert oder subtrahiert.

Grafische Vektoraddition
Vektoren werden addiert, indem durch Parallelverschiebung der Anfangspunkt des zu addierenden Vektors auf den Endpunkt eines Vektors zu liegen kommt. Der Summenvektor ist gleich dem Vektor, der vom Anfangspunkt des Ersten und Endpunkt des parallel verschobenen Vektors zeigt.
Grafische Vektorsubtraktion
Vektoren werden subtrahiert, indem der Gegenvektor des zu subtrahierenden Vektors zum ersten Vektor addiert wird.
Richtungsvektor
Ein Richtungsvektor ist durch die Koordinaten seines Anfangs- und Endpunkts bestimmt. Zu diesen beiden Punkten (A und B) können Ortsvektoren angegeben werden. Die Koordinaten des Richtungsvektors errechnen sich aus denen des Ortsvektors, der zum Endpunkt des Richtungsvektors weist, von denen die Koordinaten des Ortsvektors subtrahiert werden, der zum Anfangspunkt des Richtungsvektors weist.
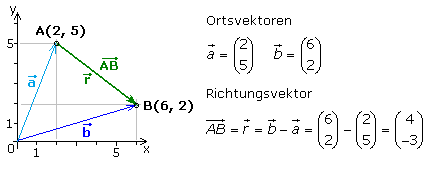 △
△
Vektorvervielfachung – Multiplikation eines Vektors mit einem Skalar
Werden n gleiche linienflüchtige Vektoren aneinander gereiht, dann ist deren Vektorsumme gleich der Multiplikation des einzelnen Vektors mit dem Skalar n. Die Richtung des Summenvektors bleibt bei positivem n erhalten. Bei negativem Skalar zeigt der Summenvektor in die 180° Gegenrichtung. Die Multiplikation mit null ergibt den Nullvektor. Die Multiplikation eines Vektors mit einem reellen Skalar wird meistens als S–Multiplikation bezeichnet.
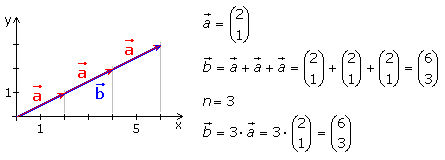
Ein Vektor wird mit einem reellen Skalar multipliziert, indem jede Vektorkoordinate mit dem Skalar multipliziert wird.
Rechenregeln zur skalaren Multiplikation
Wie bei der Multiplikation von Zahlen gelten ein gemischtes Assoziativgesetz und das Distributivgesetz, wobei die Skalare Elemente der reellen Zahlen sind. Ein Kommutativgesetz gibt es nicht, da die Multiplikation einer Zahl mit einem Vektor nicht definiert ist.
 △
△
Die Länge eines Vektors
Bei der senkrechten Projektion eines Vektors auf die Achsen eines orthogonalen kartesischen Koordinatensystems werden die einzelnen Vektorkomponenten auf die entsprechenden Achsen abgebildet. Sie können als Vielfache der Basis- oder Einheitsvektoren geschrieben werden. Mithilfe der senkrecht stehenden Vektorkomponenten und dem Satz des Pythagoras kann der Betrag des Summenvektors bestimmt werden. Nachfolgend sind die Lösungsschritte aufgezeigt. Die Quadrate der Einheitsvektoren haben den skalaren Wert 1.
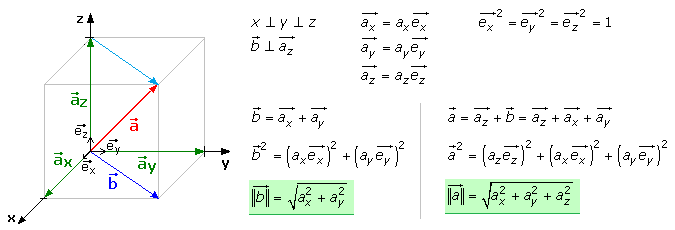
Die Länge eines Vektors, auch als sein Betrag bezeichnet, ist mathematisch die Wurzel aus der Summe der Quadrate seiner Vektorkoordinaten.
△Normierung eines Vektors
Die Normierung ist bedeutsam bei Darstellungen im Koordinatensystem. Im räumlich kartesischen Koordinatensystem haben die Einheits- oder Basisvektoren den Betrag 1 und liegen in der jeweiligen Achsenrichtung. Jedem Vektor, der kein Nullvektor ist, kann ein in seine Richtung verlaufender Einheitsvektor mit dem Betrag 1 zugewiesen werden. Die Normierung eines Vektors ergibt seinen Einheitsvektor mit gleicher Richtung aber unabhängig von der Länge. Die Vektorkoordinaten werden durch die Länge, also den Betrag des Vektors dividiert. Das Vektorsymbol, sein Bezeichner, ist ein e mit dem Index des Vektorbuchstaben oder wird als Vektorbuchstabe mit einem Dach (Zirkumflex) geschrieben. Dieser Einheitsvektor hat dann den Betrag 1.
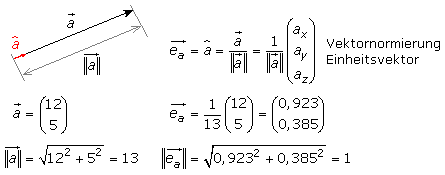 △
△
Skalarprodukt von Vektoren – Inneres Produkt
Zwei Ortsvektoren werden miteinander multipliziert indem ihre entsprechenden Vektorkoordinaten multipliziert und die einzelnen Ergebniswerte addiert werden. Das Endergebnis ist eine skalare Größe. Als eindeutiges Rechenzeichen sollte ein kleiner nicht ausgefüllter Kreis anstelle des sonst gewohnten Punkts verwendet werden. Das Ergebnis des Skalarprodukts zweier Ortsvektoren mit Längen ungleich null kann null ergeben. Ortsvektoren unterschiedlicher Richtung schließen einen Winkel ein und nachfolgend wird gezeigt, dass ihr Skalarprodukt von diesem Winkel abhängig ist. Das Bild zeigt einige Beispiele zum Skalarprodukt von Vektoren in der Ebene. Für Vektoren im Raum gelten die entsprechenden Rechenregeln.

Besteht zwischen beiden Vektoren ein spitzer Winkel, dann hat die Projektion eines Vektors auf den anderen den gleichen Richtungssinn und das Skalarprodukt ist eine positive Zahl. Bei einem stumpfen Winkel ist die Projektion antiparallel und das Skalarprodukt hat einen negativen Wert. Bilden beide Vektoren einen rechten Winkel, dann ist das Skalarprodukt null, da der Kosinus von 90° null ergibt.
Das Skalarprodukt von Vektoren ist die Summe, die sich aus der Multiplikation gleicher Spaltenkoordinaten errechnet.
Aus der Schulphysik ist bekannt, dass die Wegstrecke, die ein Köper beim Einwirken einer konstanten Zugkraft zurücklegt vom Angriffswinkel der Kraft auf den Körper abhängig ist. Je größer der Winkel zwischen der Wegrichtung und der Kraftrichtung ist, desto kürzer ist die Wegstrecke, die in der gleichen Zeit zurückgelegt wird. Die wirksame Kraft ist die senkrechte Projektion der Zugkraft auf die Wegstrecke. Für ein beliebiges, nicht rechtwinkliges Dreieck kommt der Kosinussatz der Trigonometrie zur Anwendung. Der von zwei Vektoren b und c eingeschlossene Winkel α kann mit dem Skalarprodukt recht einfach berechnet werden. Die allgemeine Herleitung ist im folgenden Bild zu sehen.
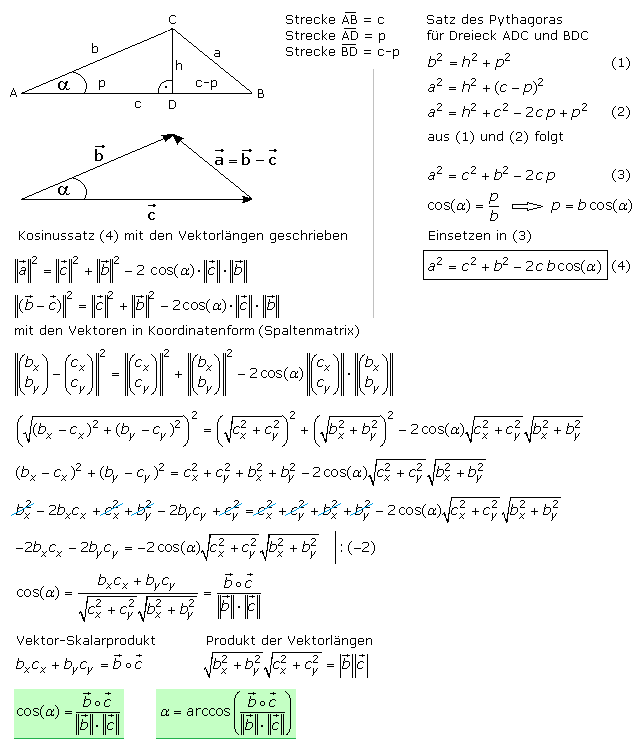
Definition: Das Skalarprodukt zweier Vektoren errechnet sich aus dem Produkt der Vektorbeträge multipliziert mit dem Kosinus des Winkels, der von den Vektoren eingeschlossen wird.
Rechenregeln zum Skalarprodukt
Es gilt das Kommutativgesetz, wo das Ergebnis unabhängig von der Reihenfolge der Vektoren ist. Es gilt das Distributivgesetz wo gleiche Vektoren aus Summen und Differenzen ausgeklammert werden können. Es gilt ein gemischtes Assoziativgesetz mit skalaren Größen als Element der reellen Zahlen.
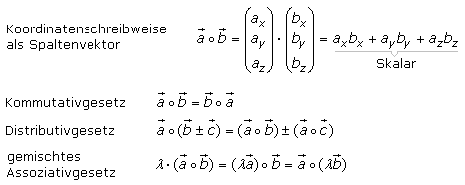
Beim Skalarprodukt eines Vektors mit sich selbst werden seine gleichen Spaltenkoordinaten multipliziert und addiert. Das Ergebnis ist ein Skalar. Wird die Länge des Vektors ermittelt und quadriert, so ist das Ergebnis gleich dem zuvor errechneten Skalar. Das Skalarprodukt eines Vektors mit sich selbst ist gleich dem Quadrat seiner Länge.

Das folgende Beispiel zeigt an zwei Vektoren in der Ebene, dass die Berechnung des Skalarprodukts mit den Spaltenkoordinaten und des Kosinussatzes gleichberechtigt ist. Weiterhin wird mithilfe des Skalarprodukts die orthogonale Stellung zweier Vektoren nachgewiesen.
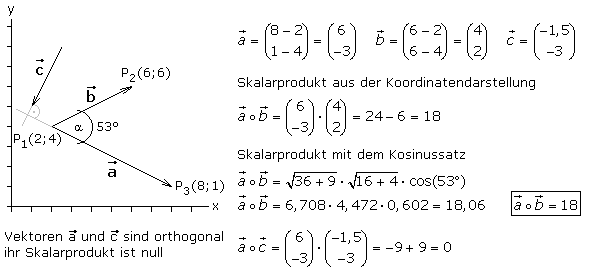
Zwei Vektoren, die keine Nullvektoren sind, verlaufen rechtwinklig (orthogonal), wenn ihr Skalarprodukt den Wert null hat.
Schnittwinkel zweier Vektoren
Mit dem Skalarprodukt in Form des Kosinussatzes kann der Schnittwinkel zweier Vektoren bestimmt werden. Die Gleichung wird nach dem Kosinus des Winkels umgestellt. Der Winkel errechnet sich mithilfe des Arcuscosinus. Bei cos(φ) = 0 ist φ = 90° ein rechter Winkel. Bei cos(φ) > 0 ist das Ergebnis ein spitzer Winkel und bei cos(φ) < 0 ein stumpfer Winkel. Bei cos(φ) = ±1 sind die Vektoren kollinear ausgerichtet, parallel in gleicher Richtung bei +1 und antiparallel bei −1.
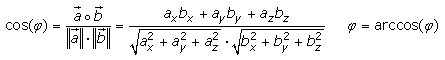
Gibt es zwischen zwei Vektoren einen Schnittwinkel, so kann mithilfe der normierten Vektoren die Winkelhalbierende berechnet werden. Die Einheitsvektoren mit dem Betrag 1 spannen einen Rhombus (eine Raute) auf, dessen Summenvektor die Winkelhalbierende c ist. Zur Verdeutlichung wurden in der Skizze die Einheitsvektoren zusätzlich mit dem Faktor 3 multipliziert und eingezeichnet. Die Berechnung des Schnittwinkels φ zwischen den Vektoren a und b ist doppelt so groß wie zwischen der Winkelhalbierenden c und dem Vektor a.
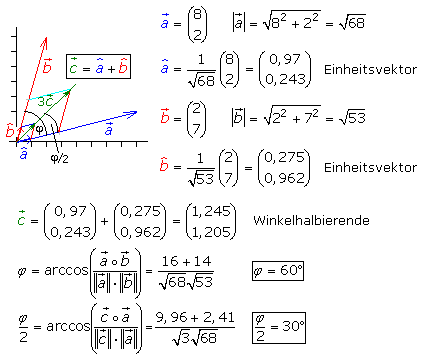 △
△
Projektion eines Vektors auf einen Vektor
Zwei Vektoren, die keine Nullvektoren sind, können zu sich parallel verschoben werden, sodass ihre Anfangspunkte zusammenliegen. Jeder der Vektoren kann durch senkrechte Projektion auf den anderen abgebildet werden. Der Projektionsvektor ba liegt in Richtung des Vektors a, auf den er projiziert wurde und unterscheidet sich von diesem nur durch einen skalaren Wert. Die Herleitung kann auf unterschiedliche Weise erfolgen.
 △
△
Vektorprodukt – Kreuzprodukt
Zwei im Raum nicht parallel liegende Vektoren, die keine Nullvektoren sind, können durch Parallelverschiebung eine Ebene aufspannen. Ihr Vektorprodukt ist ein Vektor, der senkrecht auf dieser Ebene steht. Sein Betrag ist die Maßzahl des Flächeninhalts des von den beiden Vektoren aufgespannten Parallelogramms. Zur Unterscheidung vom Skalarprodukt mit dem (speziellen) Multiplikationspunkt als Rechenzeichen wird das Vektorprodukt mit einem Multiplikationskreuz geschrieben. Gelesen wird es als a Kreuz b und als äußeres Produkt oder Kreuzprodukt bezeichnet. Das Vektorprodukt ist für den dreidimensionalen Raum definiert. Im zweidimensionalen Raum (Ebene) kann der Ergebnisvektor nicht gleichzeitig auf beiden Ausgangsvektoren stehen, die ein Parallelogramm aufspannen.
Die drei Vektoren bilden ein mathematisches Rechtssystem in der Reihenfolge a b (a x b). Haben die drei Vektoren denselben Anfangspunkt und bewegt man sich vom Vektor a über den kleineren Winkel zum Vektor b, dann ist die Richtung für den Vektor a x b der Weg, in den sich eine rechtsgängige Schraube hineindreht.
Die Richtung des Ergebnisvektors kann auch mithilfe der Drei-Finger-Regel der rechten Hand ermittelt werden. Der Daumen für a und der Zeigefinger für b spannen eine Ebene auf und ihr Vektorprodukt a x b weist in Richtung des senkrecht abgespreizten Mittelfingers. Im Vektorprodukt ist die Reihenfolge der Vektoren wichtig, denn wird sie vertauscht, so zeigt der Ergebnisvektor in die Gegenrichtung. Seine absolute Länge bleibt gleich.
Das Vektorprodukt zweier vom Nullvektor verschiedener Vektoren ist immer dann null, wenn beide Vektoren kollinear verlaufen. Das gilt auch für Vektorprodukte der Achseneinheitsvektoren mit sich selber. Für die drei Einheitsvektoren des räumlichen rechtwinkligen Achsensystems besteht ein Rechtssystem nach folgendem Schema:

Das folgende Bild veranschaulicht das Vektorprodukt und gibt die Definition zur Berechnung. An einem Beispiel wird die Richtigkeit der gemachten Aussagen nachgewiesen. Beim Aufspannwinkel von φ = 90° hat das Vektorprodukts den größten Wert. Bei einem Winkel von φ = 0° liegen die Ausgangsvektoren parallel zueinander und das Kreuzprodukt hat den Wert null. Das ist ebenso der Fall, wenn mindestens einer der Vektoren ein Nullvektor ist.
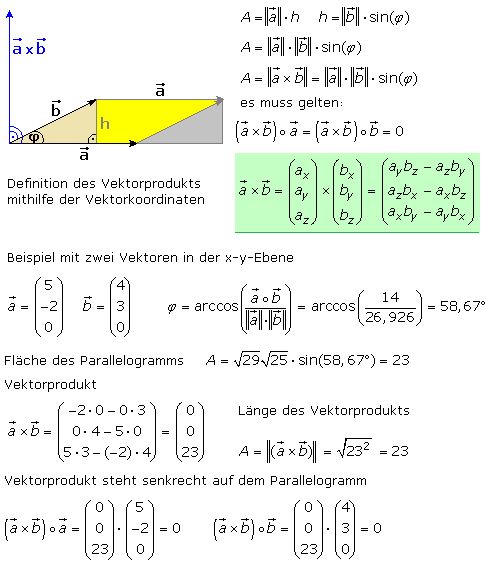
Herleitung der Vektorkoordinaten für das Vektorprodukt
Das Vektorprodukt von zwei Vektoren definiert einen Vektor der auf beiden Ausgangsvektoren senkrecht steht. Mit dieser Bedingung kann ein Gleichungssystem aufgestellt werden. Das lineare Gleichungssystem hat die drei unbekannten Koordinaten des Ergebnisvektors. Kann eine Lösung gefunden werden, dann muss das Ergebnis mit der im vorigen Abschnitt gemachten Definition des Vektorprodukts übereinstimmen. Betrachtet wird das räumlich rechtwinklige Koordinatensystem mit den Vektoren a und b und dem Vektor p als Vektorprodukt.

Vektorprodukt mit Determinanten
Zwei Vektoren im dreidimensionalen Raum können durch ihre Achsenkomponenten dargestellt werden. Die einzelnen Komponenten ergeben sich durch senkrechte Projektion jedes Vektors auf die einzelnen Achsen. Jede der Komponenten ist das Skalarprodukt des Achseneinheitsvektors mit der jeweiligen Länge der Projektion. Der Vektor ist dann die Summe seiner drei Komponenten. Wenn für das Vektorprodukt diese beiden Summen gliedweise ausmultipliziert werden können, dann muss das Ergebnis identisch mit der weiter oben gegebenen Definition für das Vektorprodukt sein.
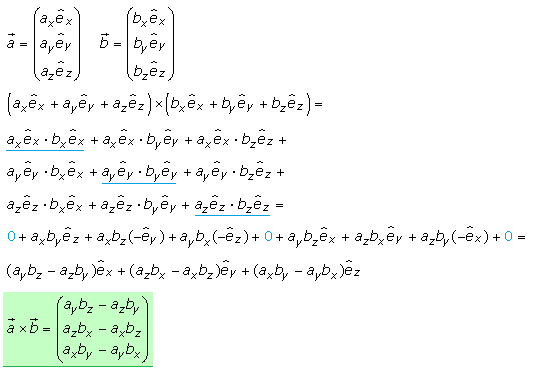
Diese Herleitungen sind nicht so leicht zu merken und rechenaufwendig. Das Ergebnis passt zum Lösungsschema einer 3x3 Determinante. Die Vektorkoordinaten einschließlich des Einheitsvektors können in Reihen- oder Spaltenanordnung geschrieben werden. Die Koordinaten des Vektorprodukts werden leicht zu merken mit der Regel nach Sarrus bestimmt.
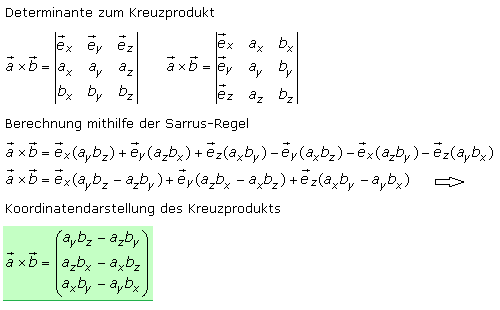
Sind Determinanten unbekannt, kann für das Kreuzprodukt zweier Vektoren das folgende Lösungsschema hilfreich sein. Die Vektorkomponenten werden in ihrer Spaltenform geschrieben. Diese wird ein weiteres Mal direkt darunter geschrieben. Die oberste und die unterste Zeile werden gestrichen. Von links werden die Diagonalwerte der zweiten und dritten Zeile multipliziert. Davon subtrahiert werden von links gelesen die Diagonalwerte der dritten und zweiten Zeile. Das Schema ebenso für die dritte und vierte Zeile und dann noch für die vierte und fünfte Zeile durchgeführt.

Rechenregeln zum Vektorprodukt
Da die drei Vektoren des Kreuzprodukts ein Rechtssystem bilden, besteht kein Kommutativgesetz. Werden die beiden Vektoren im Kreuzprodukt vertauscht, so zeigt der Ergebnisvektor in die entgegengesetzte Richtung. Das wird auch als Antikommutativgesetz bezeichnen. Anwendbar sind das Distributivgesetz und das Assoziativgesetz mit reellen Skalaren.
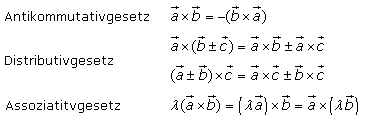 △
△
Spatprodukt
Zur Volumenberechnung eines dreidimensionalen Körpers sind Angaben zur Grundfläche und Höhe notwendig. Das entspricht drei unterschiedlichen Richtungsangaben und kann auch vektoriell berechnet werden. Die Länge des Vektorprodukts entspricht dem Flächeninhalt. Er steht senkrecht auf der Fläche und bildet mit der Höhe des Körpers einen bestimmten Winkel. Steht der Richtungsvektor der Höhe ebenfalls senkrecht auf der Fläche, dann entsprechen die Vektoren den Kanten eines Rechtecks oder bei gleichen Längen eines Würfels.
Ein schiefwinkliger Körper ist ein Parallelepiped mit sechs Seiten in Form von Parallelogrammen. Ein sehr bekanntes Beispiel ist der Kalkspat (Kalziumkarbonats CaCO3). Das Mineral bildet oft große, schiefwinklige quaderförmige Kristalle aus, die als Spatkristalle bezeichnet werden. In der Schulphysik werden an Kalkspatkristallen Versuche zur Lichtdoppelbrechung gezeigt. Nach dieser Kristallform wird das gemischte Vektorprodukt als Spatprodukt bezeichnet.
Zwei Kanten a und b eines Spatkristalls spannen als Vektoren definiert die Grundfläche auf. Das Vektorprodukt a x b steht als Flächenvektor senkrecht darauf. Das Volumen wird durch die dritte zur Fläche schiefwinklig stehende Kante bestimmt. Projiziert man diesen Kantenvektor c senkrecht auf den Flächenvektor, so ist seine Projektionslänge gleich h der Spathöhe. Das Volumen kann bei Kenntnis des eingeschlossenen Winkels φ aus den Längen des Vektorprodukts und der Länge der Höhe berechnet werden.
Der Kosinus des Schnittwinkels zweier Vektoren wurde weiter oben hergeleitet. Es ist das Skalarprodukt der Vektoren dividiert durch das Produkt beider Vektorlängen. Wird diese Definition zur Berechnung des Spatprodukts verwendet, so muss der Winkelwert nicht angegeben sein. Der Schnittwinkel wird vom Vektorprodukt, dem Flächenvektor und dem dritten Kantenvektor aufgespannt.

Das Spatprodukt ist die Skalarmultiplikation eines Vektors mit einem Vektorprodukt (Kreuzprodukt) mit dem Ergebnis eines Skalars. Da das Vektorprodukt antikommutativ ist, sollte bei einer Volumenberechnung das Ergebnis als Absolutwert angegeben werden. Das Spatprodukt kann als Determinante einer 3x3 Matrix der drei Vektoren geschrieben werden. In der Determinante können die Vektorkomponenten in der Zeilen- oder Spaltenform angeordnet sein. Mit dem Lösungsschema nach Sarrus wird die Berechnung einfach.

Rechenregeln zum Spatprodukt
Es gibt kein Kommutativgesetz. Im Spatprodukt ist das Vektorprodukt eine nicht trennbare Einheit. Der (a · b) x c ergibt keinen Sinn, denn das Ergebnis des Klammerausdrucks ist ein Skalar. Der Wert des Spatprodukts bleibt gleich, wenn die drei Vektoren zyklisch vertauscht werden, wobei die Rechenzeichen an ihrer Stelle stehen bleiben. Werden im Kreuzprodukt zwei Vektoren vertauscht, so findet ein Vorzeichenwechsel statt. Werden die Rechenzeichen vertauscht, dann müssen die Klammern verschoben werden.

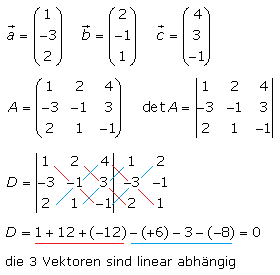
Lineare Abhängigkeit von Vektoren
Vektoren sind linear abhängig wenn ihrer Linearkombination den Nullvektor ergibt und die Vektoren keine Nullvektoren sind. Zwei Vektoren die parallel (kollinear) verlaufen, wobei ihre Richtung gleich oder entgegengesetzt sein kann, sind immer linear abhängig. Ihre Längen können gleich sein oder sie unterscheiden sich um einen beliebigen skalaren Faktor.

Drei Vektoren, die keine Nullvektoren sind und in einer Ebene liegen sind komplanar. Durch Anpassen ihrer Längen entsteht immer eine geschlossene Vektorverkettung. Sie sind linear abhängig, wenn die Linearkombination den Nullvektor ergibt. Es wird ein lineares Gleichungssystem (LGS) aufgestellt. Die Skalarfaktoren werden berechnet. Ist mindestens einer der Faktoren ungleich null, so sind die Vektoren linear abhängig.
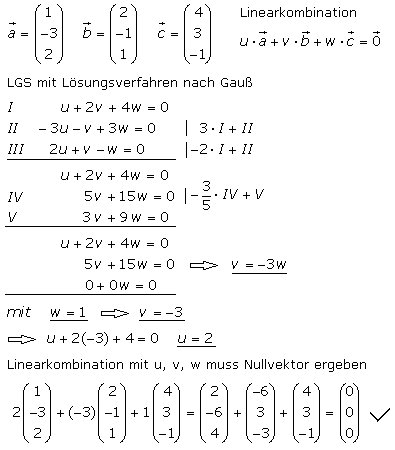
Mithilfe des Spatprodukts kann die lineare Abhängigkeit von drei Vektoren überprüft werden. Die Vektoren sind linear abhängig und liegen in einer Ebene wenn die Determinante der 3x3 Matrix der Koordinatenwerte den Wert null hat. Verglichen mit dem LGS können mit diesem Verfahren die Skalarfaktoren nicht bestimmt werden.