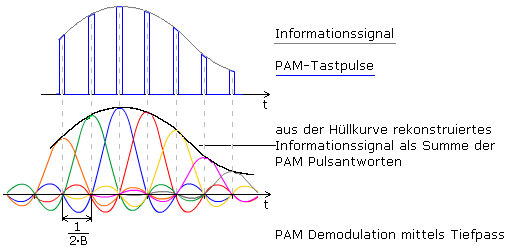
Pulsamplitudenmodulation – PAM
- Pulsamplitudenmodulation - PAM
- Abtasttheorem nach Shannon
- Das Zeitmultiplexverfahren
- Demodulation eines PAM-Signals
Bei der bereits beschriebenen analogen Amplitudenmodulation wird die Amplitude eines sinusförmigen Trägers proportional zum niederfrequenten Informationssignal moduliert. Die Pulsmodulations-, auch PM-Verfahren genannt, verwenden als Nachrichtenträger pulsförmige Signale. Das Trägersignal ist nicht mehr zeitkontinuierlich, sondern ein zeitdiskreter, periodischer schmaler Rechteckpuls.
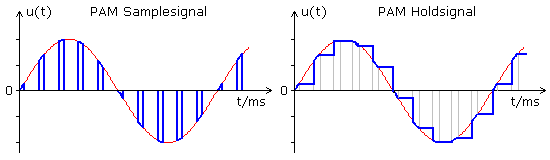
Werden die Trägerpulse bezogen auf das Nachrichtensignal als Schaltintervalle gesehen, so lassen sich zeitdiskrete Ausschnitte aus der Information heraus tasten. Im einfachsten Fall einer solchen Abtastung erhält man das PAM-Signal. Der Tastpuls nimmt den zum Tastzeitpunkt aktuellen Amplitudenwert der Information an.
Das PAM-Verfahren wird normalerweise nicht zur direkten Signalübertragung eingesetzt. Es ist eine wichtige Vorstufe zur Erzeugung weiterer Pulsmodulationsarten wie beispielsweise der Pulscode-(PCM)-, Pulsdauer-(PDM)- und Pulsphasen-(PPM)-Modulation. Für Amplitudenstörungen ist die PAM ebenso anfällig wie die analoge AM.
Durch die Wahl der Modulations- oder Abtastschaltung kann eine unipolare oder bipolare PAM erhalten werden. Bei der unipolaren PAM wird vor der Abtastung das Informationssignal mittels Gleichspannung über die Nulllinie hinaus verschoben. In der Übertragungstechnik wird die bipolare PAM bevorzugt. Ein Vierquadranten-Multiplizierer-IC kann als universeller Modulator für beide PAM-Signale verwendet werden.
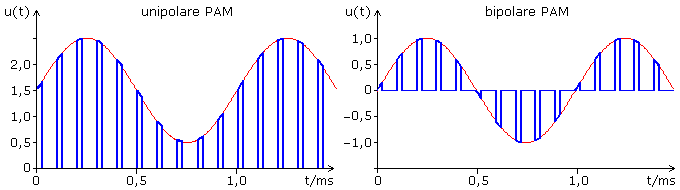
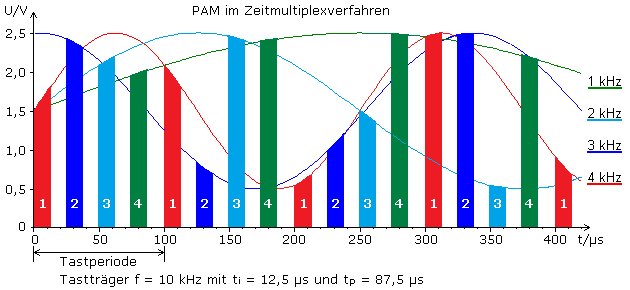
Beide PAM-Signale (blau) entstanden bei der Abtastung einer 1 kHz Sinusinformation (rot) mit einem 10 kHz rechteckförmigen Tastträger. Der zur Veranschaulichung groß gewählte Tastgrad von 25% zeigt, dass ein PAM-Signal zeitdiskret aber in den Tastwerten wertekontinuierlich ist.
Die Charakteristik eines Schaltvorgangs entspricht einer gewinkelten und somit gekrümmten Kennlinie. Die Überlagerung wird dadurch zur Modulation und mathematisch mithilfe der Multiplikation der Signalfunktionen beschrieben. Wie bei der Amplitudenmodulation treten auch im Frequenzspektrum des Modulationsprodukts der PAM neben der Trägerfrequenz obere und untere Seitenfrequenzen auf. Sie lassen sich aus den Summen und Differenzen zwischen den Träger- und Informationsfrequenzen errechnen.
Nach Fourier weist der Trägerpuls ein eigenes Frequenzspektrum mit Harmonischen der ganzzahligen Vielfachen seiner Grundfrequenz auf. Das Spektrum des PAM-Signals zeigt somit für alle Trägerharmonischen symmetrisch angeordnete Seitenbänder.
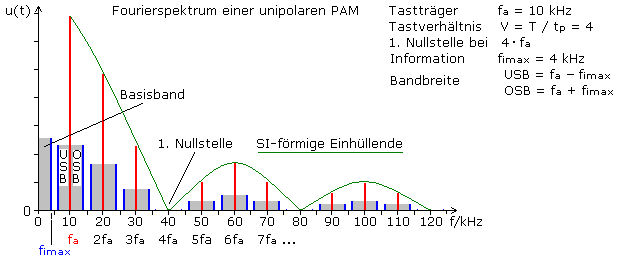
Im Frequenzspektrum einer bipolaren PAM fehlen die Spektrallinien des Trägers, ansonsten entspricht es dem oben gezeigten Bild. Verglichen mit dem Spektrum einer normalen AM, ist neben den höheren modulierten Harmonischen des Tastträgers hier das Erscheinen des Basisbands der Information auffällig. Es ist in jedem PAM-Signal enthalten und bei der unipolaren PAM kommt noch der Gleichanteil hinzu.
Hinweis: Die gezeigten Diagramme wurden mit der Simulationssoftware Multisim erstellt. Die Ergebnisse der Fourieranalysen entsprachen trotz genauer Eintragungen der Versuchsparameter in vielen Fällen nicht den Erwartungen. Eine versuchsweise Verminderung der Grundfrequenzangabe ergab qualitativ richtige Spektren. Die absoluten y-Achsenwerte erwiesen sich dann als unbrauchbar.
△Abtasttheorem nach Shannon
Ein Informationssignal mit begrenzter Bandbreite kann eindeutig durch eine Anzahl diskreter Werte bestimmt werden. Jede nichtsinusförmige periodische Zeitfunktion lässt sich nach Fourier durch ein Spektrum einer Grundschwingung und den Oberwellen als ganzzahligen Vielfachen der Grundfrequenz fmin, beschreiben. Durch die 1. Harmonische ist der zeitliche Abstand T = 1 / fmin der Frequenzlinien bestimmt.
Da die Information in ihrer Bandbreite B begrenzt sein soll, können im Spektrum der PAM aber nicht unendlich viele Oberwellen auftreten. Aus der oberen Grenzfrequenz und dem kleinstmöglichen Abstand der Frequenzlinien kann die Zahl der maximal vorkommenden Frequenzen errechnet werden. Dieser Wert ist zu verdoppeln, da eine Schwingung nach Amplitude und Phasenlage durch die Summe einer Cosinus- und Sinusschwingung gleicher Frequenz mit entsprechend gewählten Amplituden erzeugt werden kann. Mit der Anzahl der Schwingungen: n = 2 · B · T sind dann pro Sekunde n / T Schwingungswerte zu übertragen. Mit dem oben errechneten n erhält man als Ergebnis 2·B numerische Werte pro Sekunde.
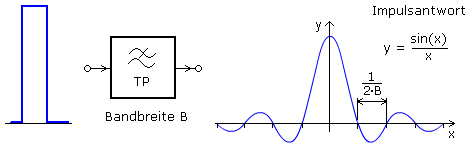
Aus den diskreten Tastwerten kann das ursprüngliche, analoge Signal nur dann zurückgewonnen werden, wenn bei der Abtastung die Tastfrequenz fT etwas mehr als doppel so hoch, wie die höchste auftretende Signalfrequenz fi max ist. Mit einem idealen Tiefpass lässt sich dann aus dem Tastsignal das Basisband unverfälscht ausfiltern. Diese Regel wurde 1949 von C.E.Shannon aufgestellt und das Abtasttheorem nach ihm bekannt.
Abtasttheorem nach Shannon: fT > 2 · fi max
oder
TTast < 1 / 2 · Ti min
Grenzfrequenz des Tiefpass:
fg = 1 / 2 · fT Nyquistfrequenz.
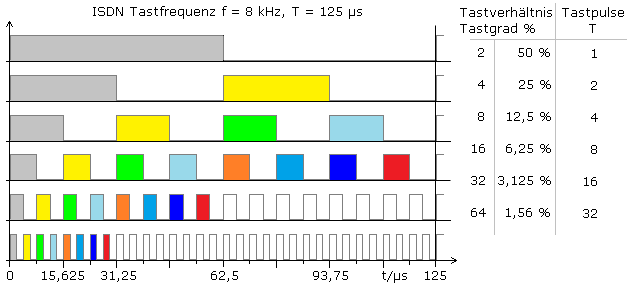
Wie anfangs gezeigt, genügen theoretisch genau zwei Tastwerte für eine Signalperiode, um das Signal zu rekonstruieren. Da es praktisch keinen Tiefpass mit rechteckig steiler Flanke gibt, muss die Tastfrequenz mehr als den doppelten Wert der höchsten Informationsfrequenz haben. Für die zwei folgenden Beispiele ist das Shannon-Theorem erfüllt. Die Sprachbandbreite der ISDN-Telefonie reicht bis 3400 Hz und wird mit 8 kHz abgetastet. Das Audiofrequenzband reicht bis 20 kHz und wird vor der Digitalisierung mit mindestens 44,1 kHz abgetastet.
Aliasingeffekt
Bei der Unterabtastung wird das Abtasttheorem mit einer zu niedrigen Tastfrequenz nicht eingehalten. Das folgende Beispiel zeigt das Frequenzspektrum einer unipolaren PAM bis zur 1. Nullstelle, wo mit einem 10 kHz Tastträger ein 7 kHz Signal abgetastet wurde. Die negativen Auswirkungen der Unterabtastung sind eindeutig erkennbar.
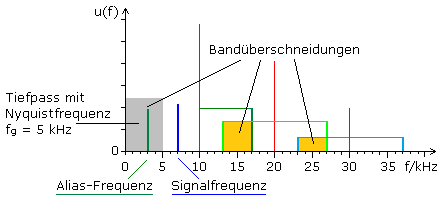
Die Demodulation zur Rückgewinnung des NF-Signals verwendet einen Tiefpass mit der zum Tastträger passenden Nyquistfrequenz. Das ursprüngliche Signal von 7 kHz liegt oberhalb dieser Grenzfrequenz und wird nicht erfasst. Stellvertretend, aliasing, erhält man ein tiefer frequentes Signal mit 3 kHz aus dem unteren Seitenband der 1. Tastharmonischen. Eine fehlerhafte Unterabtastung führt zur Überlappung der Seitenbänder. Sie ist im Bild für die 2. und 3. Tastharmonische eingezeichnet. Die Überschneidung ist der Grund für neue, im Originalsignal nicht vorhandene Frequenzen, die beim Ausfiltern des Basisbandes anstelle der höheren Originalfrequenzen erscheinen.
Vor der Abtastung werden mögliche Frequenzanteile oberhalb der halben Tastfrequenz durch einen Tiefpass, dem Anti-Aliasing-Filter, aus dem Signal entfernt. Da es keine idealen Filter gibt, ist dessen Grenzfrequenz bei festgelegter Tastfrequenz niedriger als die Nyquistfrequenz.
△