RC-Sinusoszillator
Ein Oszillator ist eine Schaltung, die nach dem Anlegen einer Gleichspannung als Betriebsspannung selbsttätig ein periodisches Ausgangssignal erzeugt. Die Schaltung muss die unvermeidlichen Verluste selbst ausgleichen können, da sonst nur eine gedämpfte, abklingende Schwingung entsteht.
Beschrieben wird ein RC-Oszillator mit anschließender mathematischer Herleitung des Übertragungsfaktors und der Oszillatorfrequenz. Ein Oszillator ist eine Verstärkerschaltung mit einem frequenzabhängigen Rückkopplungsnetzwerk, das die Eigenschaft der Signal-Mitkopplung erfüllt. Eine zusätzliche Regelschaltung hält die Schleifenverstärkung konstant und verhindert die Resonanzkatastrophe. In diesem Webprojekt findet man auch grundlegende Informationen zur Rückkopplung und Regelung.
RC-Phasenschieber
Jedes als Hoch- oder Tiefpass geschaltetes RC-Glied erzeugt eine Phasenverschiebung zwischen dem Ein- und Ausgangssignal, die innerhalb von absolut 0 ... 90° liegt. Eine Reihenschaltung mit mindestens drei gleich dimensionierten RC-Gliedern erreicht für eine bestimmte Frequenz eine 180° Phasendrehung, wenn jede Stufe für sich die Phase um 60° dreht. Dieses Netzwerk nennt sich RC-Phasenschieberkette und arbeitet als Rückkopplungsnetzwerk in einer Verstärkerschaltung. Invertiert der Verstärker sein Eingangssignal, so ist die Bedingung einer Mitkopplung erfüllt und die Schaltung wird zum Oszillator.
Phasenschiebergenerator
Als Verstärker eignet sich ein Transistor in Emitterschaltung oder ein invertierender Operationsverstärker. Sein Ausgangssignal gelangt über die Phasenschieberkette an den Eingang des Verstärkers zurück. Für eine bestimmte Frequenz, der Oszillatorfrequenz, wird die Summe der Phasendrehungen 0° oder 360° und das System erzeugt ein Sinussignal. Das folgende Bild zeigt die beiden prinzipiellen Schaltungen.
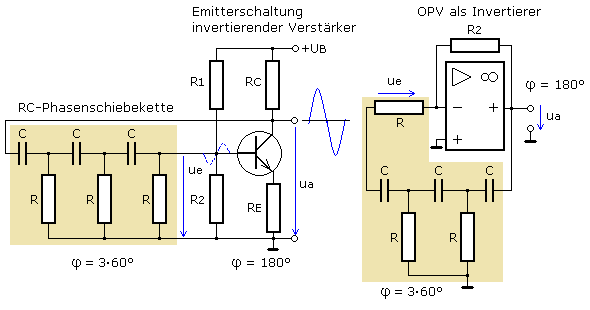
Der Ausgangswiderstand des Verstärkers sollte sehr klein gegenüber dem Eingangswiderstand der Phasenschieberkette sein. Der Eingangswiderstand des Verstärkers darf das Rückkoppelnetzwerk nicht belasten und muss groß im Vergleich zu R sein. In der Transistorschaltung kann der rechte Widerstand der Phasenschieberkette auch entfallen, wenn der dynamische Eingangswiderstand des Transistors dem Widerstandswert R entspricht. Der Wert errechnet sich zu: re ≈ R1 || R2 || (rBE + β·RE).
Für Schaltungen mit Operationsverstärkern sind die Widerstandsverhältnisse besser erfüllt. Der Ausgangswiderstand des Invertierers ist naturgemäß niedrig und der Eingangswiderstand des beschalteten OPVs wird hier durch R bestimmt. Der invertierende Eingang dieser Schaltung bildet die virtuelle Masse, daher kann auf einen Ankoppelwiderstand zwischen der Phasenschieberkette und dem OPV verzichtet werden.
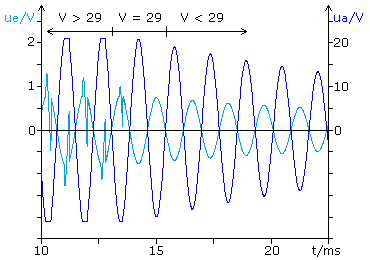
Die Funktionsweise dieser OPV-Schaltung wurde mit einem Simulationsprogramm untersucht. R2 ist durch einen 1 MΩ einstellbaren Widerstand mit einprozentiger Wertverstellung ersetzt. Die Phasenschieberkette ist mit dreimal R = 10 kΩ und C = 10 nF dimensioniert. Nach dem Einschalten der Simulation muss der Verstärkungsfaktor V > 29 sein. Die anschließende Verringerung lässt ab V < 29 die Schwingung zusammenbrechen. Oberhalb dieses Wertes geht das Sinussignal in die Begrenzung, da diese Schaltung über keinen Regelkreis verfügt.
Beide oben dargestellten Schaltungen erfüllen die Phasenbedingung φ=0° für die Mitkopplung. Sie müssen das Eingangssignal soweit verstärken, dass auch die Schleifen- oder Ringverstärkung mit k·V = 1 für eine stabile Schwingung erfüllt ist. Der oben gezeigte Phasenschieber stellt eine Reihenschaltung drei gleicher Hochpässe dar, da die Ausgangsspannung für das Folgeglied an R abgegriffen wird. Der folgende Hochpass belastet mit seiner Impedanz diesen Quellenwiderstand und verringert die Ausgangsspannung des vorangehenden Hochpasses. Insgesamt wird dadurch die Eingangsspannung der Kette um den Faktor 29 geschwächt. Der Verstärker muss diese hohe Verstärkung aufbringen, damit es nicht zur gedämpften Schwingung kommt.
Für die OPV-Simulationsschaltung wurden für jeden einzelnen Hochpass die Phasenwinkel zwischen ihren Eingangs- und Ausgangsteilspannungen bestimmt. Die Ausgangsspannung des OPVs wurde vom ersten Hochpass um 55° in der Phase gedreht. Sie ist für den zweiten HP die Eingangsspannung und wurde um 57° in der Phase gedreht. Der dritte HP drehte seine Eingangsspannung dann um gemessene 68°. Die Phasenwinkelsumme ergibt die notwendigen 180°. Trotz der gegenseitigen Belastung teilte sich die Phasendrehung erstaunlich gleichmäßig auf die drei Pässe auf.
Der Videoclip zeigt für drei gleich dimensionierte Stufen einer RC-Kette mit idealisierten animierten Zeigerdiagrammen die Phasenverhältnisse, die zum Erhalt der Oszillatorfrequenz notwendig sind. Damit sich die Pässe nicht gegenseitig belasten, wurden sie in der Simulation durch zwischengeschaltete (nicht dargestellte) Impedanzwandler entkoppelt. Für jedes einzelne RC-Glied ist bei einer Phasenverschiebung von 60° die Ausgangsspannung nur noch halb so groß wie die Eingangsspannung. Aus dem Spannungsverhältnis errechnet sich dann die Abschwächung der gegenseitig entkoppelten RC-Glieder zu k = 8. Für die Oszillatorfrequenz gilt die Beziehung f = 1 / (2π·√3·RC) = 919 Hz.
RC-Phasenschieber sind einfach aufzubauen und lassen sich zur Erzeugung sehr niedriger Frequenzen dimensionieren. Der Bau abstimmbarer Oszillatoren dagegen ist schwieriger, da immer drei Widerstände oder Kondensatoren wertegleich geändert werden müssen. Auch eine stabile Amplitudenregelung für ein Sinussignal mit geringem Klirrfaktor erweist sich als aufwendig. Wesentlich bessere Eigenschaften und einfacher zu handhaben ist der Wien-Robinson oder Wien-Brückengenerator, ein weiterer RC-Oszillator.
△Herleitung des Übertragungsfaktors und der Oszillatorfrequenz
Die in Reihe geschalteten RC-Pässe der Phasenschieberkette beeinflussen sich gegenseitig. Jede Folgestufe belastet mit ihrer Impedanz den Ausgang der Vorstufe. Das hat Auswirkungen auf die Ausgangsspannung und die Oszillatorfrequenz bei der Gesamtphasendrehung von 180°.
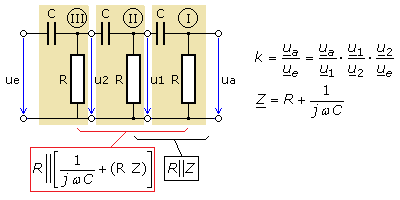
Betrachtet man nur den HP(I), so liegt die Ausgangsspannung am Widerstand R und die Eingangsspannung u1 an der Reihenschaltung von R und C. Nach dem Aufstellen der Übertragungsfunktion wird der Nenner auf seinen Hauptnenner gebracht. Die Gleichung wird umgeformt, wobei noch die Zeitkonstante τ vereinfachend eingeführt wird.
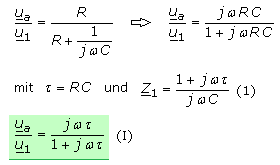
Die Ausgangsspannung u1 des HP(II) wird durch die Impedanz des HP(I) Gl.(1) belastet. Sie liegt daher an der Parallelschaltung aus R und Z. Die Berechnung von R||Z erfolgt mit den Leitwerten. Die Eingangsspannung u2 liegt an der Reihenschaltung von C und dem komplexen Leitwert dieser Parallelschaltung, deren Impedanz jetzt verwendet werden muss. Das zweite Spannungsverhältnis ist proportional zum Verhältnis der entsprechenden Impedanzen.
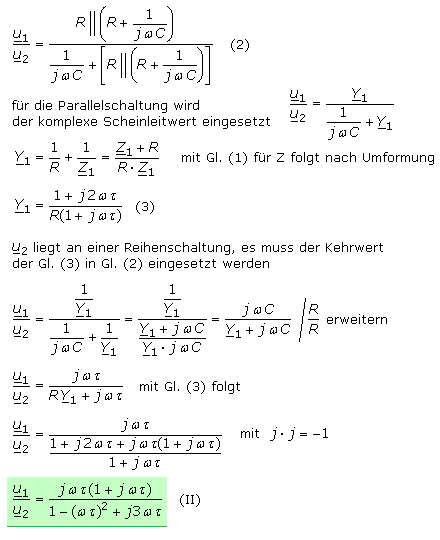
Entsprechende Verhältnisse gelten für den HP(III). Sein R liegt parallel zur Impedanz Z des HP(II), dessen Widerstand R mit der Impedanz des HP(I) eine Parallelschaltung bildet. Die Eingangsspannung wiederum liegt an der Impedanz des HP(I). Bei den Teilschaltungen sind die mehrfachen Wechsel zwischen Impedanz und Leitwert zu beachten. Das Spannungsverhältnis wird mit den Impedanzen aufgestellt.
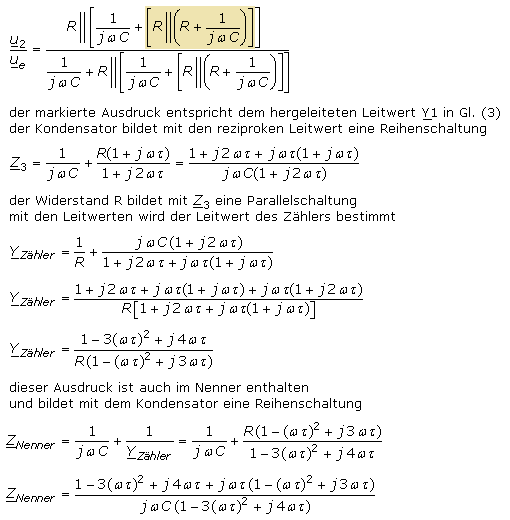
Das Spannungsverhältnis wird mit den komplexen Impedanzen ZZähler und ZNenner hergeleitet.

Mit den drei Teilgleichungen (I), (II) und (III) errechnet sich der komplexe Übertragungsfaktor k. Eine der Resonanzbedingungen, die das frequenzabhängige Koppelnetzwerk erfüllen muss, ist der Phasenwinkel mit φ = 180°. Wenn im Spannungsverhältnis eine Spannung ausschließlich reell ist, dann ist die invertierte andere Spannung ebenfalls reell. Es muss sich folglich eine Frequenz, die Oszillatorfrequenz, errechnen lassen, bei der die imaginären Anteile von k den Wert null ergeben. Die zweite Schwingbedingung mit k·V = 1 muss ebenfalls erfüllt sein. Mit der jetzt bestimmbaren Oszillatorfrequenz kann die notwendige Ringverstärkung V errechnet werden.

Die mit dieser umfangreichen Herleitung ermittelbaren Ergebnisse werden durch Messungen an aufgebauten Schaltungen und der Auswertung einer Schaltungssimulation bestätigt. Die ermittelte Oszillatorfrequenz betrug für die oben untersuchte Schaltung f0 = 630 Hz. Die errechnete Frequenz ergibt 650 Hz. Die Mindestverstärkung wurde ebenfalls experimentell bestätigt.
Der Wien-Robinson-Generator, auch als Wien-Brückengenerator bezeichnet, ist eine weitere Oszillatorschaltung mit einem RC-Netzwerk, das aus zwei gleichwertig dimensionierten Hoch- und Tiefpässen besteht.