Überlagerung periodischer Signale
Befinden sich in einer Schaltung mehrere Gleichspannungs- und/oder Gleichstromquellen, so dann kann die Ausgangsgröße unter Berücksichtigung der Vorzeichen durch eine einfache Addition errechnet werden. Es gelten die beiden Kirchhoffschen Regeln. Bei der Addition mehrerer periodischer AC-Quellensignale sind der zeitliche Verlauf und die jeweilige Phasenlage zu berücksichtigen. Sind die zu addierenden Signale im linearen Amplituden-Zeitdiagramm dargestellt, so können für jeden Zeitpunkt die Momentanwerte unter Beachtung der Vorzeichen addiert und in das Diagramm eingezeichnet werden. Das Verbinden aller neuen Punkte ergibt das lineare Amplituden-Zeitdiagramm des Ausgangssignals.
Addition gleichfrequenter Sinussignale
In Schaltungen mit Blindwiderständen überlagern sich oft Sinussignale gleicher Frequenz mit unterschiedlichen Maximalamplituden und Phasenlagen. Die Addition sinusförmiger Signale gleicher Frequenz kann einfach mithilfe eines rotierenden Zeigerdiagramms konstruiert werden. Die im Ursprung und Drehpunkt fest zueinander angeordneten Zeiger rotieren entgegen dem Uhrzeigersinn mit der Signalfrequenz. Die Zeigerlänge ist von der Maximalamplitude und der Phasenwinkel vom Winkel des Zeigers zur Horizontalen bestimmt. Die Zeiger werden, wie für Vektoren bekannt, geometrisch addiert und bilden den Summenzeiger. Alle Zeiger rotieren mit der gleichen Frequenz entgegen dem Uhrzeigersinn um den Kreismittelpunkt. Für jeden Zeitpunkt oder Rotationswinkel kann ein rechtwinkliges Dreieck von der Zeigerspitze zum Achsenkreuz gezeichnet werden. Die Projektion des Zeigers auf die Vertikale entspricht dem Momentanwert einer Sinuskurve und die Projektion des Zeigers auf die Horizontale dem einer Kosinuskurve. Die zusammengehörigen Momentanwerte werden in ein Liniendiagramm mit horizontaler Zeit- oder Winkelunterteilung eingetragen. Ihre Verbindungen bilden den jeweiligen Signalverlauf. Im Amplituden-Zeitdiagramm kann für jedes Signal der Phasenwinkel und zu jedem Zeitpunkt oder Drehwinkel der Momentanwert abgelesen werden.
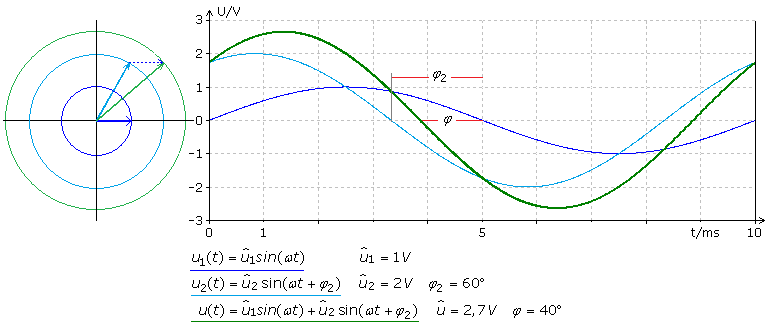
Die Grafik zeigt das Simulationsergebnis der additiven Überlagerung von zwei Sinusspannungen unterschiedlicher Amplituden an einem ohmschen Widerstand mit linearer Kennlinie. Die Frequenz beträgt f = 100 Hz. Der Phasenwinkel des kleineren Signals (blau) beträgt 0°. Zu ihm ist das größere Signal (hellblau) um +60° in der Phase gedreht. Das Summensignal (grün) hat mit 100 Hz die gleiche Frequenz. Der Spitzenwert kann zu rund 2,7 V und der Phasenwinkel mit +40° zum kleineren Signal abgelesen werden.
Es gibt auch rein mathematische Lösungen zur additiven Überlagerung sinusförmiger Signale. Für zwei gleichfrequente Sinussignale unterschiedlicher Amplituden und Phasenwinkel wird schrittweise die Formel zur Berechnung hergeleitet.

Das lineare Zeitdiagramm weiter oben zeigt die additive Überlagerung gleichfrequenter Sinussignale unterschiedlicher Amplitude wobei nur ein Signal einen von null abweichenden Phasenwinkel hat. Das sinusförmige Summensignal hat einen neuen Spitzenwert und einen neuen Phasenwinkel. Beide Werte können mit den hergeleiteten Formeln Gl. (4) und Gl. (5) berechnet werden und stimmen mit den im Diagramm abgelesenen Werten überein.
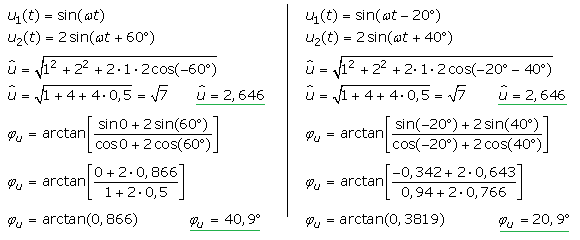
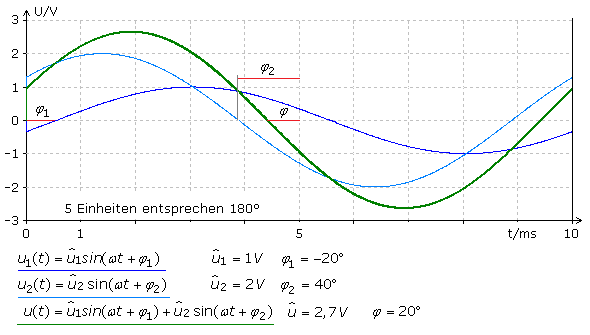
Bei der folgenden Simulation wurden zwei gleichfrequente Sinussignale unterschiedlicher Amplituden und von null verschiedener Phasenwinkel additiv überlagert. Die Phasenwinkel wurden so gewählt, dass das Ergebnis mit der ersten Simulation verglichen werden kann. Werden 20° zum Phasenwinkel φ1 und φ2 und dem Phasenwinkel φu des Summensignals addiert, dann wären die Signaldiagramme deckungsgleich.
Wird das Summensignal einer linearen Überlagerung mithilfe eines Frequenzanalysators untersucht, so lassen sich die Parameter der Ausgangssignale ablesen. Das Gerät vollzieht die Fourieranalyse und somit die Umkehrung der Fouriersynthese. Die Fouriersynthese ist die (lineare) additive Überlagerung periodischer Signale wobei keine neuen Frequenzen entstehen. Mit Simulationssoftware kann fast immer die Fourieranalyse durchgeführt werden.
Addition von Sinussignalen mit größerem Frequenzunterschied
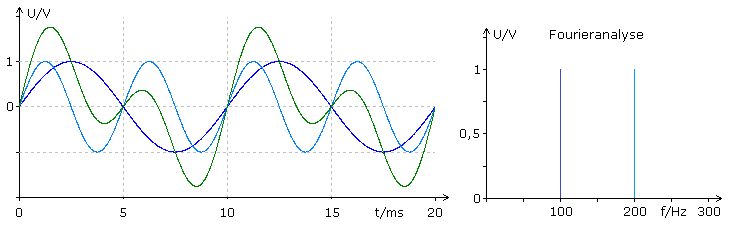
Die Grafik zeigt die Zeitdiagramme zweier Sinussignale mit 100 Hz (blau) und 200 Hz (hellblau). Diese Signale werden linear additiv zum grünen Summensignal überlagert. Für jeden gewählten Zeitpunkt sind seine Amplitudenwerte gleich der Summe der Momentanwerte der Eingangssignale. Die Periodizität des Summensignals ist von der niedrigsten Signalfrequenz bestimmt. Mit der Fourieranalyse des Summensignals können die Frequenzen und Amplitudenverhältnisse der Eingangssignale ermittelt werden.
Das folgende Diagramm zeigt die additive Überlagerung der Sinussignale mit f = 1 kHz und Û = 1 V mit f = 10 kHz und Û = 2 V. Das Ausgangssignal ist periodisch. Die denkbare Hüllkurve ist von der niedrigeren Frequenz bestimmt. Die dargestellten (inneren) Kurvenzüge sind mit der höheren Frequenz periodisch. Die Fourieranalyse zeigt die beiden Eingangsfrequenzen und die Maximalamplituden der Eingangssignale. Im Tonbeispiel (mono) ist erst ein 1 kHz Ton danach ein 8 kHz Ton und dann das gemeinsame Überlagerungssignal zu hören. Es können deutlich zwei Frequenzen herausgehört werden.
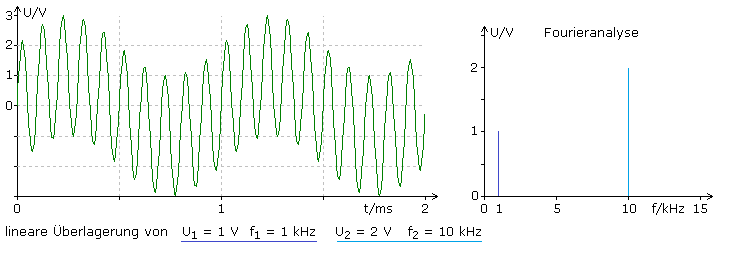
Addition zweier Sinussignale mit kleinerem Frequenzunterschied
Im folgenden Audiobeispiel sind erst die einzelnen Sinustöne mit 5 kHz und 4 kHz zu hören und danach ihr additives Überlagerungssignal. Im Vergleich zum vorigen Beispiel sind im Summensignal die Einzelfrequenzen kaum noch getrennt wahrnehmbar. In einer Simulation wurden zwei Sinussignale additiv überlagert. Das Signal mit der höheren Frequenz f = 10 kHz und der größeren Amplitude Û = 2,5 V ist vom Sinussignal mit f = 9 kHz und der kleineren Amplitude Û = 1,5 V additiv überlagert.
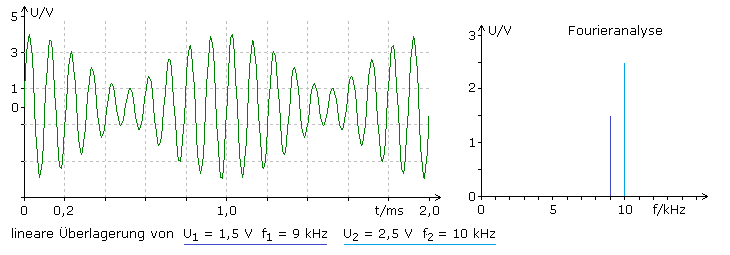
Im Zeitdiagramm sieht das Überlagerungssignal einem AM-Signal (Amplitudenmodulation) mit dem Modulationsgrad m = 0,6 ähnlich. Da in der Fourieranalyse die obere Seitenbandlinie bei 11 kHz fehlt, handelt es sich um eine lineare Signalüberlagerung und keine Amplitudenmodulation. Bei einer Amplitudenmodulation werden die Eingangssignale an einer gekrümmten Kennlinie multiplikativ überlagert. Das Fourierdiagramm zeigt dann drei zueinander symmetrisch angeordnete Frequenzlinien.
Addition zweier Sinussignale mit sehr kleinem Frequenzunterschied
Per Simulation werden zwei Sinussignale mit gleicher Amplitude und Phasenlage additiv überlagert, deren Frequenzen sehr nahe beieinander liegen. Das Summensignal hat im Nulldurchgang keinen Phasensprung, der bei einem AM-Signal mit unterdrücktem Träger auftritt. Da auch die Fourieranalyse keine neuen Frequenzen, sondern nur die beiden Eingangsfrequenzen und ihre Amplituden zeigt, handelt es sich auch hier um eine additive Signalüberlagerung.
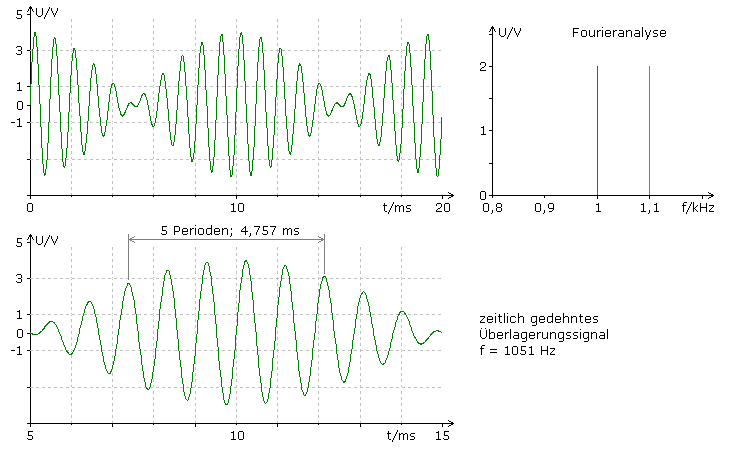
Die Überlagerung erzeugt eine Schwebung. In der Audiotechnik kann mithilfe der zu hörenden Schwebung ein Frequenzabgleich durchgeführt werden. Der Referenzton wird meistens von einer Stimmgabel vorgegeben und mit dem Tonsignal der zu prüfenden zweiten Quelle überlagert. Bei Frequenzgleichheit ist der Ton der Stimmgabel mit konstanter Lautstärke zu hören. Stimmen die Frequenzen nicht überein, so schwankt die Lautstärke periodisch. Im dargestellten Beispiel hat die gedachte Hüllkurve die Periodendauer T = 20 ms und die Frequenz f = 50 Hz. Das Ohr interpretiert die Amplitudenänderung der gedachten Hüllkurve als Schwebungsfrequenz. Die Überlagerungsfrequenz errechnet sich aus dem Mittelwert der Eingangsfrequenzen. Die maximale Amplitude entspricht der Summe der Spitzenamplituden der Eingangssignale. Im Tonbeispiel sind Schwebungen mit der Standardfrequenz des Kammertons a = 440 Hz in den Abstufungen 445 Hz, 442 Hz, 441 Hz, 440,5 Hz und zum Schluss mit Frequenzgleichheit 440 Hz zu hören.
Die gedachte Hüllkurve ist die Verbindung aller minimalen oder maximalen Spitzenwerte. Die Frequenz errechnet sich als absoluter Mittelwert aus der Differenz der beiden sich überlagernden Frequenzen. Die im Diagramm sichtbare Frequenz des Summensignals, auch resultierende Frequenz genannt, wurde in der Simulation bei gedehnter Zeitbasis ermittelt. Sie errechnet sich als Mittelwert aus der Summe der sich überlagernden Frequenzen. Die mathematische Herleitung zeigt diese Zusammenhänge für Eingangssignale gleicher Amplitude und Nullphasenwinkel.

Aus dem Diagramm der Simulation wurde für die resultierende Summenfrequenz f = 1051 Hz ermittelt. Die Hüllkurvenfrequenz f = 50 Hz ist der Kehrwert der Periodendauer, der mit 20 ms abgelesen werden kann. Für die Simulationsfrequenzen betragen die genauen mathematischen Werte für das Additionssignal f = 1050 Hz und für die Hüllkurve f = 50 Hz. Je geringer der Frequenzunterschied zwischen den Eingangssignalen ist, desto weiter liegen die Nulldurchgänge im Überlagerungssignal auseinander. Bei Frequenzgleichheit gibt es keine Lautstärkeschwankungen mehr.
Multiplikative Überlagerung zweier Sinussignale
In analog arbeitenden Schaltungen beeinflusst eine niedrige Signalfrequenz, als NF-Signal bezeichnet, die Amplitude einer wesentlich höheren Trägerfrequenz, HF-Signal genannt. Die Amplitude des NF-Signals sollte immer kleiner als die des HF-Signals sein. Das Ergebnis ist ein Gemisch aus den Eingangssignalen und einem hochfrequenten Überlagerungssignal (Modulationssignal) mit neuen Eigenschaften. Wird für die Modulation eine Rechnerschaltung, zum Beispiel ein Vierquadranten Multiplizierer verwendet, dann ist das Ausgangssignal das optimale definierte Amplituden moduliertes (AM) Signal. Haben beide Eingangssignale keinen DC-Offset, so bildet sich das Modulationssignal als AM mit unterdrücktem Träger. Hat ein Eingangssignal ein DC-Offset, dann entsteht ein (normales) AM-Signal mit Träger. In beiden Ausgangssignalen ist weder die NF-Frequenz noch sind andere Oberwellen vorhanden. Die Fourieranalyse des Modulationssignal zeigt symmetrisch zur Lage der Trägerfrequenz zwei neue Frequenzen, die als untere (HF-Frequenz minus NF-Frequenz) und obere (HF-Frequenz plus NF-Frequenz) Seitenfrequenz bezeichnet werden.
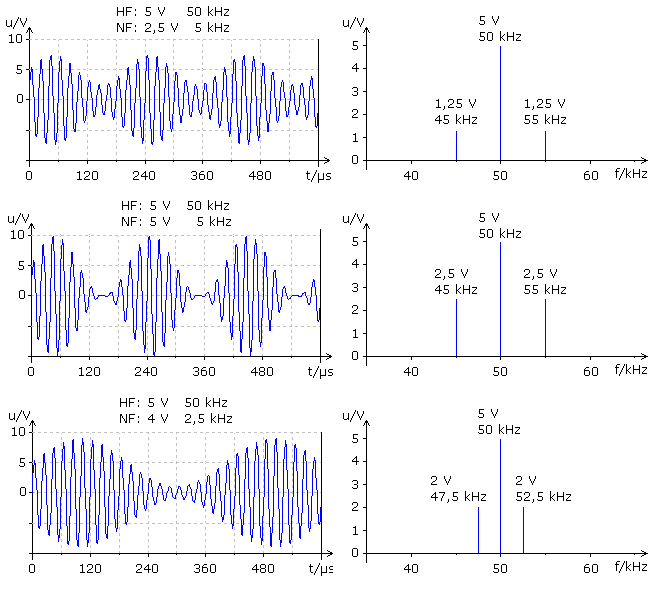
Die Simulationsergebnisse zeigen die Überlagerung eines NF-Signals mit DC-Anteil und eines HF-Signals am Vierquadranten Multiplizierer als Zeitdiagramme mit den zugehörigen Fourieranalysen. Im Zeitdiagramm kann die HF-Frequenz aus den zeitlich gleichbleibenden periodischen Schwingungen bestimmt werden. Die NF-Frequenz kann aus der Periodizität der gedachten Hüllkurve im positiven oder negativen Bereich bestimmt werden. Die beiden Amplituden der Eingangssignale können ebenfalls im Zeitdiagramm abgelesen werden. Haben beide Signale die gleiche Amplitude, dann wird die HF-Trägeramplitude bis zur Nulllinie von der NF-Amplitude beeinflusst. Das Verhältnis der NF-Amplitude zur HF-Amplitude ist der Modulationsgrad m und kann zwischen 0 ... 1 liegen. Sendesignale im Mittelwellenbereich sind (waren) AM-Signale mit einem maximalen Modulationsgrad um m = 0,6.
Die Fourieranalyse zeigt, dass die multiplikative Überlagerung (Modulation) neue Frequenzen erzeugt. Aus den Höhen der Frequenzlinien können die Signalamplituden abgelesen werden, wobei jede Seitenlinie die halbe NF-Amplitude hat. Der Modulationsgrad ist die Summe der Höhe beider Seitenlinien dividiert durch die Höhe der HF-Trägerfrequenzlinie. In diesem Webprojekt gibt es ausführliche Informationen zur Amplitudenmodulation und zur Zweiseitenband AM sowie weitere spezielle AM-Verfahren, der Restseitenband-AM und der Einseitenband-AM.
Bestimmen der Phasenwinkel mit dem Oszillograph
Steuert ein AC-Signal eine elektronische Schaltung an, so kann das Ausgangssignal eine andere Phasenlage haben. Liegt der Phasenwinkel zwischen 10 ... 80°, kann die Bestimmung mit guter Genauigkeit mithilfe eines Oszillographen erfolgen. Eine Phasenwinkelbestimmung ist nur für Signale gleicher Frequenz sinnvoll. Der folgende Videoclip zeigt die Phasenverschiebung für ein Sinussignal konstanter Frequenz in 15°-Schritten zwischen ±180°. Die Bezugsphase der blauen Kurve beträgt 0°. Es ist zu erkennen, dass innerhalb einer Periode der Streckenanteil der Verschiebung auf der horizontalen Achse zweimal auftritt. Ist diese Achse im Winkelgrad oder dem entsprechenden Bogenmaß skaliert, so kann durch das Streckenverhältnis einer Teilstrecke bezogen auf die Gesamtstrecke für die halbe Periode der aktuelle Phasenwinkel errechnet werden. Das Ablesen der Teilstrecke muss in dem Bereich erfolgen, wo beide Kurvenzüge mit positiver oder negativer Steigung den gleichen Steigungsverlauf haben. Im Video werden für jeden Schritt die aktuellen Werte angezeigt. Ob es sich bei ±180° um eine Phasenverschiebung oder eine Inversion des Signals handelt, kann mit einer einfachen Messung per Oszillograph nicht eindeutig bestimmt werden.
Das Ablesen am Oszillograph wird besonders einfach, wenn die horizontale Kalibrierung nicht genutzt wird. Voraussetzung für eine korrekte Messung ist die deckungsgleiche Nulllinie beider Messkanäle. Auf den Nulldurchgang der Bezugskurve wird getriggert und die halbe Periode wird manuell auf horizontal genau 9 Teiler (DIV) eingestellt. Damit entspricht jeder Einzelne 20° und jeder Teilstrich dazwischen 4°. Der Phasenwinkel kann durch Addition der Teileinheiten schnell abgelesen werden. Beginnt links die phasenverschobene Kurve oberhalb der Horizontalen, dann ist der Phasenwinkel positiv und das Ausgangssignal verhält sich vorlaufend. Beginnt die Kurven unterhalb der Horizontalen, so ist der Phasenwinkel negativ mit nachlaufendem Ausgangssignal.