Passive RC- und RL-Hochpässe

Ein passiver Hochpass unterscheidet sich vom ausführlich beschriebenen Tiefpass im Wesentlichen durch die vertauschte Anordnung der Bauteile. Es handelt es sich um frequenzabhängige Spannungsteiler. Beim RC-Hochpass liegt die Ausgangsspannung parallel am ohmschen Wirkwiderstand und beim RL-Hochpass parallel zum induktiven Blindwiderstand. Die folgenden Betrachtungen gelten für sinusförmige Eingangssignale mit konstanter Amplitude und variabler Frequenzen.

Der RC-Hochpass

Beim RC-Hochpass ist nur der kapazitive Blindwiderstand Xc von der Frequenz abhängig. Am ideal angenommenen Kondensator eilt der Strom um φ = 90° der Spannung voraus. In der Reihenschaltung ist der Strom die Bezugsgröße und zeigt im Zeigerdiagramm wie angedeutet horizontal nach rechts. Die Zeiger für die Spannung am Kondensator und der dazu proportionale Zeiger des Blindwiderstands zeigen folglich senkrecht nach unten.

Mit zunehmender Frequenz wird der Blindwiderstand des Kondensators kleiner. Die Zeigerlänge der an Xc proportionalen Spannung nimmt ab. Da die Eingangsspannung u1 konstant hat der dazu proportionale Zeiger Z der Impedanz eine konstante Länge und dreht sich in Richtung zur realen Achse des ohmschen Wirkwiderstands. Daraus folgt, dass die Zeigerlänge der Ausgangsspannung u2 am Wirkwiderstand zunimmt. Der Phasenwinkel zwischen u2 an R und u1 an Z verändert sich von φ = +90° zu φ = 0°.

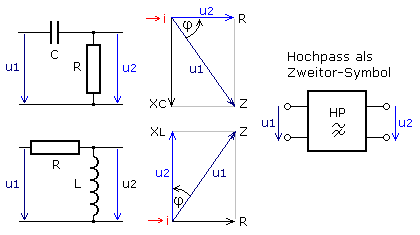
Der RL-Hochpass

Beim RL-Hochpass ist nur der induktive Blindwiderstand XL von der Frequenz abhängig. Die Ausgangsspannung wird an der Spule abgenommen. Bei einer ideal angenommenen Induktivität eilt die Spannung um φ = 90° dem Strom voraus. Der Zeiger des Blindwiderstands zeigt senkrecht nach oben. Der Wert des induktiven Blindwiderstands nimmt zu höheren Frequenzen linear zu. Die Spannung an der Induktivität verhält sich direkt proportional zum Wert ihres Blindwiderstands.

Mit zunehmender Frequenz der Eingangsspannung dreht sich der dazu proportionale Zeiger Z mit konstanter Länge in Richtung der Vertikalen zum Spannungszeiger des induktiven Blindwiderstands. Der Wert der Ausgangsspannung u2 nähert sich dem der konstanten Eingangsspannung u1 an. Der Phasenwinkel zwischen der u2 und u1 verändert sich dabei von φ = +90° zu φ = 0°.

Bodediagramm

Für jeden Hochpass gibt es die definierte Grenzfrequenz fg. Bei ihr haben der Wirkwiderstand und der Blindwiderstand den gleichen Wert. Der Phasenwinkel zwischen der Ausgangsgröße in Bezug zur Eingangsgröße beträgt φ = +45°. Das Verhältnis der Ausgangs- zur Eingangsgröße hat bei der Grenzfrequenz den charakteristischen Wert 0,707 entsprechend −3 dB.

Hochpässe mit nur einem Typ Blindwiderstand sind Pässe oder Filter 1. Ordnung. Die Ausgangsgröße hat die charakteristische Dämpfung von 6 dB pro Oktave oder 20 dB pro Dekade. Die grafische Bestimmung mit einem Steigungsdreieck muss im Kennliniendiagramm weit genug unterhalb der Grenzfrequenz im linearen Bereich der Kennlinie erfolgen. Die folgenden Diagramme zeigen für einen RC- und RL-Hochpass mit gleicher Grenzfrequenz den von der Eingangsfrequenz abhängigen Amplituden- und Phasenfrequenzgang der Ausgangsspannung in Bezug zur Eingangsspannung.

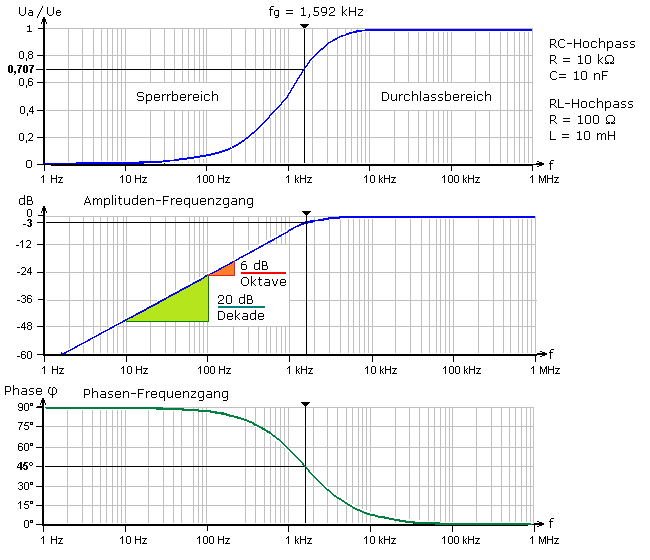
Die Übertragungsfunktionen

Übertragungsfunktion für einen RC-Hochpass

Die Bezugsgröße ist eine in der Amplitude konstante und in der Frequenz variable Eingangsspannung. Sie liegt an der Reihenschaltung von R und C, der Impedanz Z der Schaltung. Die Ausgangsspannung wird beim RC-Hochpass am ohmschen Widerstand abgegriffen. Die Übertragungsfunktion ist das Verhältnis der Ausgangsgröße zur Eingangsgröße. Der Vergleich unterschiedlich dimensionierter Schaltungen ist mit einer normierten Übertragungsfunktion leichter möglich. Die Ausgangsgröße bei passiven Schaltungen kann maximal den Wert 1 oder 100% annehmen. Normiert wird die Übertragungsfunktion indem sie mit 1/R erweitert wird. Im Nenner kann der Faktor vor der Wurzel als quadratischer Faktor in die Wurzel einbezogen werden. Der Ausdruck unter der Wurzel wird ausmultipliziert. Das Ergebnis ist die normierte Übertragungsfunktion: \[\frac{{{U_a}}}{{{U_e}}} = \frac{R}{Z}\quad Z = \sqrt {{R^2} + X_c^2} \quad {X_c} = \frac{1}{{\omega \,C}} = \frac{1}{{2\,\pi \,f\,C}}\] \[\frac{{{U_a}}}{{{U_e}}} = \frac{R}{{\sqrt {{R^2} + X_c^2} }} \cdot \frac{{{\textstyle{1 \over R}}}}{{{\textstyle{1 \over R}}}}\quad \Rightarrow \quad \frac{{{U_a}}}{{{U_e}}} = \frac{1}{{\sqrt {\frac{1}{{{R^2}}}\left( {{R^2} + X_c^2} \right)} }}\] \[\frac{{{U_a}}}{{{U_e}}} = \frac{1}{{\sqrt {1 + {{\left( {\frac{{{X_c}}}{R}} \right)}^2}} }}\quad \Rightarrow \quad \frac{{{U_a}}}{{{U_e}}} = \frac{1}{{\sqrt {1 + \frac{1}{{{{(\omega \,R\,C)}^2}}}} }}\quad (1)\] In der Gl.(1) ist nur der Wert des kapazitiven Blindwiderstands XC von der Frequenz abhängig. Bei der Grenzfrequenz fg sind die Widerstandswerte von R und XC gleich groß und die Amplitude der Ausgangsspannung erreicht rund 71% der Eingangsamplitude, siehe Gl.(2).\[\frac{{{U_a}}}{{{U_e}}} = \frac{1}{{\sqrt 2 }} \approx 0,707\quad (2)\] Die Grenzbetrachtungen für Eingangsfrequenzen gegen null und gegen unendlich stimmen mit dem Kurvenverlauf des Amplituden-Frequenzgangs aus dem Bodediagramm überein. Zum Hochpass Ausgang werden bevorzugt die hohen Frequenzen übertragen. \[\begin{array}{l} f \to 0\quad \Rightarrow \frac{{{U_a}}}{{{U_e}}} = \frac{1}{{\sqrt {1 + \infty } }} \approx \frac{1}{\infty } \approx 0\quad \Rightarrow \frac{{{U_a}}}{{{U_e}}} \to 0\\ f \to \infty \quad \Rightarrow \frac{{{U_a}}}{{{U_e}}} \approx \frac{1}{{\sqrt {1 + 0} }} \approx 1\quad \Rightarrow \frac{{{U_a}}}{{{U_e}}} \to 1 \end{array}\]

Übertragungsfunktion mit komplexer Wechselstromrechnung

Die Herleitung erfolgt mit den Operatoren und der Normierung auf die Ausgangsgröße, d. h. Zähler und Nenner werden durch R dividiert. \[{\underline G _{j\omega }} = \frac{{{{\underline U }_{aus}}}}{{{{\underline U }_{ein}}}} = \frac{R}{{\underline Z }} = \frac{R}{{R + \frac{1}{{j\,\omega \,C}}}}\] \[{\underline G _{j\omega }} = \frac{1}{{1 + \frac{1}{{j\,\omega \,R\,C}}}} = \frac{1}{{1 - j\left( {\frac{1}{{\omega \,R\,C}}} \right)}}\quad (3)\] Die Grenzwertbetrachtung für die aufgestellte Übertragungsfunktion Gl.(3) zeigt, dass es sich beim Amplituden-Frequenzgang um einen Hochpass handelt. \[\begin{array}{l} \omega \to 0\quad \Rightarrow \left( {\frac{1}{{\omega \,R\,C}}} \right) \to \infty \\ \left| {1 - j \cdot \infty } \right| \to \infty \quad \left| {{{\underline G }_{j\omega }}} \right| \to \frac{1}{\infty } \to 0 \end{array}\] \[\begin{array}{l} \omega \to \infty \quad \Rightarrow \left( {\frac{1}{{\omega \,R\,C}}} \right) \to 0\\ \left| {1 - j \cdot 0} \right| \to 1\quad \left| {{{\underline G }_{j\omega }}} \right| \to \frac{1}{1} = 1 \end{array}\]

Für den RC-Hochpass wird der normierte komplexe Ansatz so umgeformt, dass der komplexe Nenner entfällt. Dazu wird Gl.(3) konjugiert komplex erweitert und die Realkomponente (Re) von der Imaginärkomponente (Im) getrennt geschrieben: \[{\underline G _{j\omega }} = \frac{{1 + j\left( {\frac{1}{{\omega \,R\,C}}} \right)}}{{{1^2} + {{\left( {\frac{1}{{\omega \,R\,C}}} \right)}^2}}} = \frac{1}{{1 + \frac{1}{{{{(\omega \,R\,C)}^2}}}}} + j\left( {\frac{{\frac{1}{{\omega \,R\,C}}}}{{1 + \frac{1}{{{{(\omega \,R\,C)}^2}}}}}} \right)\] Der Nenner wird auf einen Hauptnenner gebracht, sodass die Real- und Imaginärkomponente nochmals umgeformt werden können: \[{\underline G _{j\omega }} = \frac{{{{(\omega \,R\,C)}^2}}}{{1 + {{(\omega \,R\,C)}^2}}} + j\left( {\frac{{\omega \,R\,C}}{{1 + {{(\omega \,R\,C)}^2}}}} \right)\] Damit können für den Amplituden- und Phasen-Frequenzgang übersichtliche Bestimmungsgleichungen aufgestellt werden: \[\left| {{{\underline G }_{j\omega }}} \right| = \sqrt {{{{\mathop{\rm Re}\nolimits} }^2} + {{{\mathop{\rm Im}\nolimits} }^2}} \] \[\left| {{{\underline G }_{j\omega }}} \right| = \sqrt {{{\left( {\frac{{{{(\omega \,R\,C)}^2}}}{{1 + {{(\omega \,R\,C)}^2}}}} \right)}^2} + {{\left( {\frac{{\omega \,R\,C}}{{1 + {{(\omega \,R\,C)}^2}}}} \right)}^2}} \] Der Ausdruck unter der Wurzel wird zusammengefasst und im Zählerausdruck neu ausgeklammert zu: \[\left| {{{\underline G }_{j\omega }}} \right| = \sqrt {\frac{{{{(\omega \,R\,C)}^2}\left( {1 + {{(\omega \,R\,C)}^2}} \right)}}{{{{\left( {1 + {{(\omega \,R\,C)}^2}} \right)}^2}}}} \] Der Bruch kann gekürzt werden. Werden Zähler und Nenner durch den Zähler dividiert folgt mit Gl.(4) der schon durch Gl.(1) bekannte Amplituden-Frequenzgang: \[\left| {{{\underline G }_{j\omega }}} \right| = \sqrt {\frac{1}{{1 + \frac{1}{{{{(\omega \,R\,C)}^2}}}}}} = \frac{1}{{\sqrt {1 + \frac{1}{{{{(\omega \,R\,C)}^2}}}} }}\quad (4)\] Im komplexen Zeigerdiagramm kann für jeden Zeiger eine Real- und Imaginärkomponente gezeichnet werden. Der Phasenwinkel errechnet sich aus dem Arcustangens des Verhältnisses der Imaginär- zur Realkomponente: \[\varphi = \arctan \left( {\frac{{{\mathop{\rm Im}\nolimits} }}{{{\mathop{\rm Re}\nolimits} }}} \right) = \frac{{\frac{{\omega \,R\,C}}{{1 + {{(\omega \,R\,C)}^2}}}}}{{\frac{{{{(\omega \,R\,C)}^2}}}{{1 + {{(\omega \,R\,C)}^2}}}}} = \frac{{\omega \,R\,C}}{{{{(\omega \,R\,C)}^2}}}\] \[\varphi = \arctan \left( {\frac{1}{{\omega \,R\,C}}} \right)\quad (5)\]

In Formelwerken und wissenschaftlichen Veröffentlichungen sind die Herleitungen oft auf die Grenzfrequenz normiert. Mit der Definition von Ω, dem Verhältnis der Kreisfrequenz ω zur Grenzkreisfrequenz ωo hat die Übertragungsfunktion bei ωo den Wert 1. Diese Normierung macht die Formelterme übersichtlicher. Die Gl.(3) für den RC-Hochpass wird umgeformt. Bei der Grenzfrequenz ist der Wert des ohmschen Widerstands gleich dem des Blindwiderstands und für ωo gibt es eine Bestimmungsgleichung: \[{\underline G _{j\omega }} = \frac{{j\,\omega \,R\,C}}{{1 + j\,\omega \,R\,C}}\quad \quad R = {X_c} = \frac{1}{{{\omega _o}C}}\quad \to {\omega _o} = \frac{1}{{R\,C}}\] In der Übertragungsfunktion wird auf ω die Definition für Ω angewendet: \[\Omega = \frac{\omega }{{{\omega _o}}}\quad \Rightarrow \quad {\underline G _\Omega } = \frac{{j\,\Omega \,{\omega _o}\,R\,C}}{{1 + j\,\Omega \,{\omega _o}\,R\,C}} = \frac{{j\,\Omega }}{{1 + j\,\Omega }}\] Es wird konjugiert komplex erweitert und der Ausdruck in den Real- und Imaginärteil getrennt geschrieben: \[\begin{array}{l} {\underline G _\Omega } = \frac{{j\,\Omega \,(1 - j\,\Omega )}}{{(1 + j\,\Omega )(1 - j\,\Omega )}} = \frac{{{\Omega ^2} + j\,\Omega }}{{1 + {\Omega ^2}}}\\ {\underline G _\Omega } = \frac{{{\Omega ^2}}}{{1 + {\Omega ^2}}} + j\left( {\frac{\Omega }{{1 + {\Omega ^2}}}} \right)\quad (6) \end{array}\] Für den Amplituden-Frequenzgang bei der Grenzfrequenz mit Ω = 1 errechnet sich er erwartete Wert −3 dB: \[\begin{array}{l} \left| {{{\underline G }_\Omega }} \right| = \sqrt {{{{\mathop{\rm Re}\nolimits} }^2} + {{{\mathop{\rm Im}\nolimits} }^2}} = \sqrt {\frac{{{\Omega ^4} + {\Omega ^2}}}{{{{(1 + {\Omega ^2})}^2}}}} \\ \Omega = 1\quad \Rightarrow \left| {{{\underline G }_\Omega }} \right| = \sqrt {\frac{2}{4}} = \frac{1}{{\sqrt 2 }} \approx 0,707 \end{array}\] Der Phasen-Frequenzgang berechnet sich zu: \[\varphi = \arctan \left( {\frac{{{\mathop{\rm Im}\nolimits} }}{{{\mathop{\rm Re}\nolimits} }}} \right)\quad \varphi = \arctan \left( {\frac{1}{\Omega }} \right)\quad (7)\]

Bei der normierten Grenzfrequenz mit Ω = 1 errechnet sich der Phasenwinkel zu φ = 45°. 1/Ω ist proportional zu 1/f. In Gl.(7) nimmt für sehr niedrige Frequenzen das Argument der Arcus-Tangensfunktion sehr große Werte an und der Phasenwinkel strebt gegen 90°. Für sehr hohe Frequenzen streben die Werte im Argument gegen null und somit φ gegen 0°. Die hergeleiteten Beziehungen beschreiben das Verhalten einer RC-Hochpassschaltung.

Übertragungsfunktion für einen RL-Hochpass

Die Ausgangsspannung beim RL-Hochpass liegt am induktiven Blindwiderstand, während die Eingangsspannung an der Reihenschaltung von R und L und somit an der Impedanz Z liegt. Die mathematische Herleitung der Übertragungsfunktion für den RL-Hochpass erfolgt entsprechend angepasst wie beim RC-Hochpass. \[\begin{array}{l} \frac{{{U_a}}}{{{U_e}}} = \frac{{{X_L}}}{Z}\quad {X_L} = \omega L\quad Z = \sqrt {{R^2} + X_L^2} \\ \frac{{{U_a}}}{{{U_e}}} = \frac{{{X_L}}}{{\sqrt {{R^2} + X_L^2} }} = \frac{1}{{\frac{1}{{{X_L}}}\sqrt {{R^2} + X_L^2} }} \end{array}\] \[\frac{{{U_a}}}{{{U_e}}} = \frac{1}{{\sqrt {1 + {{\left( {\frac{R}{{{X_L}}}} \right)}^2}} }} = \frac{1}{{\sqrt {1 + {{\left( {\frac{R}{{\omega \,L}}} \right)}^2}} }}\] Bei der Grenzfrequenz sind die Widerstandswerte von R und XL gleich und die Ausgangsspannung ist um −3 dB kleiner als die Eingangsspannung \(\frac{{{U_a}}}{{{U_e}}} = \frac{1}{{\sqrt 2 }} \approx 0,707\). Für Eingangsfrequenzen gegen null ist der Blindwiderstand und folglich die Ausgangsspannung sehr klein: \[\omega \to 0\quad \Rightarrow \frac{{{U_a}}}{{{U_e}}} \approx \frac{1}{{\sqrt {1 + \frac{R}{0}} }} \approx \frac{1}{{\sqrt {1 + \infty } }} \approx 0\] Für sehr hohe Eingangsfrequenzen ist der Blindwiderstand der Induktivität groß und bestimmt die Ausgangsspannung: \[\omega \to \infty \quad \Rightarrow \frac{{{U_a}}}{{{U_e}}} \approx \frac{1}{{\sqrt {1 + \frac{R}{\infty }} }} \approx \frac{1}{{\sqrt {1 + 0} }} = 1\]

Herleitung mit komplexer Wechselstromrechnung

Die Herleitungen für die auf die Grenzfrequenz Ω normierten komplexen Übertragungsfunktionen eines RL-Hochpasses sind vergleichbar mit den Schritten für den RC-Hochpass. \[{\underline G _{j\omega }} = \frac{{{{\underline U }_a}}}{{{{\underline U }_e}}} = \frac{{j\,\omega \,L}}{{R + j\,\omega \,L}} = \frac{1}{{1 + \frac{R}{{j\,\omega \,L}}}}\] Mit der Normierung auf die Grenzfrequenz gilt: \[R = {X_L} = {\omega _o}\,L\quad \Rightarrow {\omega _o} = \frac{R}{L}\quad \Omega = \frac{\omega }{{{\omega _o}}}\] Entsprechend in die Gleichung eingesetzt und den Nenner durch konjugiert komplexe Erweiterung real gemacht ergibt: \[{\underline G _\Omega } = \frac{{j\,\Omega }}{{1 + j\,\Omega }} = \frac{{{\Omega ^2} + j\,\Omega }}{{1 + {\Omega ^2}}}\] Aufgelöst in die Real- und Imaginärkomponente ergeben sich in übersichtlicher Form die Ausgangsgleichungen zur Berechnung des Amplituden- und Phasenfrequenzgangs: \[{\underline G _\Omega } = \frac{{{\Omega ^2}}}{{1 + {\Omega ^2}}} + j\frac{\Omega }{{1 + {\Omega ^2}}}\quad \quad \varphi = \arctan \left( {\frac{1}{\Omega }} \right)\]

Beim RC-Hochpass wird die Ausgangsspannung am ohmschen Wirkwiderstand abgegriffen.
Beim LR-Hochpass wird die Ausgangsspannung am induktiven Blindwiderstand abgegriffen.
Eingangssignale mit hohen Frequenzen durchlaufen beide Schaltungen fast ungehindert.
Eingangssignale mit niedrigen Frequenzen werden stark gedämpft.
Bei der Grenzfrequenz fg (fo) gilt Uaus = 0,707·Uein. Die Dämpfung beträgt 3 dB, die Verstärkung −3 dB.
Bei f « fg beträgt die Dämpfung 6 dB/Oktave das entspricht 20 dB/Dekade.
Bei fg beträgt der Phasenwinkel der Ausgangsspannung bezogen auf die Eingangsspannung φ = 45°.

Diese Eigenschaften gelten nur für unbelastete Pässe, wo weder der Innenwiderstand der Signalquelle noch der Eingangswiderstand einer am Ausgang angeschlossenen Folgestufe zu berücksichtigen ist. Diese Verhältnisse lassen sich durch vor- und nachgeschaltete Impedanzwandler erreichen. Ohne diese sogenannten Pufferschaltungen verringert sich die maximal erreichbare Ausgangsspannung mit zunehmender Belastung und die Grenzfrequenz nimmt andere Werte an. Im Kapitel zum belasteten RC-Pass sind die entsprechenden Untersuchungen und Herleitungen mit komplexer Wechselstromrechnung beschrieben.