Der Parallelschwingkreis
Ein Stromkreis mit zwei sich gegenseitig ergänzenden Energiewandlern und Energiespeichern erzeugt nach einer einmaligen Energiezufuhr gedämpfte Resonanzschwingungen. Der Vorgang ist im Kapitel Einführungen zum Schwingkreis anschaulich dargestellt. Ein einfacher elektrischer Schwingkreis enthält die passiven Bauteile Kondensator und Spule. In den meisten Fällen kann der Kondensator als ideales Bauteil gesehen werden. Die Spule hat mit ihrem zusätzlichen Drahtwiderstand ein weniger ideales Verhalten. Ein einmalig zugeführter kurzer Energieimpuls regt den Schwingkreis zur gedämpften Schwingung mit seiner charakteristischen Eigenfrequenz an. Abhängig von der Güte der Bauteile klingt die Schwingung mehr oder weniger schnell aus.
Wird ein Schwingkreis dauerhaft mit Energie aus einer breitbandigen AC-Signalquelle versorgt, dann zeigt die Schaltung eine ausgeprägte Signalamplitude bei ihrer Resonanzfrequenz. Kann sie durch einstellbare Kapazitäts- oder Induktivitätswerte variiert werden, so kann aus dem elektromagnetischen Frequenzgemisch vieler Rundfunk- und Fernsehkanäle ein gewünschter Sender mit der darin enthaltenen Information herausgefiltert werden.
Die Reihenschaltung von R, L und C ist im Kapitel Reihenschwingkreis ausführlich beschrieben. Im Parallelschwingkreis bilden die Bauteile Kondensator und Spule eine Parallelschaltung. Da der Drahtwiderstand der Spulen mit dem induktiven Blindwiderstand eine Reihenschaltung bildet, muss zur genauen Berechnung des Parallelschwingkreises diese Reihenschaltung in ihre äquivalente Parallelschaltung umgerechnet werden. Praktisch genügt es, die Umrechnung nur für den Reihenwiderstand durchzuführen.
Die Eigenschaften des Parallelschwingkreises werden für den Fall der Fremdanregung untersucht. Mit einer niederohmigen Signalquelle verbunden belastet dieser Innenwiderstand den Parallelschwingkreis so stark, dass keine nutzbare Resonanzstelle zu erkennen ist. Die Signalquelle muss über einen hochohmigen Vorwiderstand entkoppelt angeschlossen werden. Mit diesem Vorwiderstand zusammen verhält sie sich als Konstantstromquelle. Sie belastet den Schwingkreis umso geringer je höher der Quelleninnenwiderstand im Vergleich zum äquivalenten Drahtwiderstand der Spule ist. Die Schaltungssimulation liefert den im Bild dargestellten Amplituden- und Phasenfrequenzgang des Parallelschwingkreises.
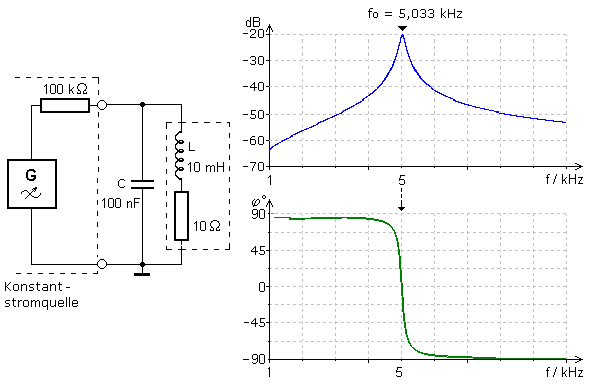
Bei konstanter Generatorspannung wird die Frequenz kontinuierlich geändert. Mit zunehmender Frequenz wird die Spannung am Schwingkreis größer, erreicht bei der charakteristischen Resonanzfrequenz fo ihr Maximum und nimmt danach wieder ab. Auf das Eingangssignal mit φ = 0° bezogen durchläuft der Phasenwinkel des Ausgangssignals am Schwingkreis den Bereich von φ = +90° bis φ = −90° mit φ = 0° bei der Resonanzfrequenz. Über einen großen Frequenzbereich betrachtet ist der Kurvenverlauf zu beiden Seiten der Resonanzfrequenz nicht symmetrisch. Oftmals wird nur der wichtigere Bereich um das Maximum herum aufgenommen, wo der Kurvenverlauf symmetrisch erscheint.
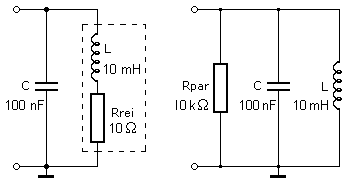
Die Schaltung zeigt den realen Parallelschwingkreis mit der Reihenschaltung aus der Induktivität und ihrem Verlustwiderstand parallel zur Kapazität, dessen Güte um einige hundertmal größer ist. Zur genauen Berechnung der Resonanzfrequenz muss die Reihenschaltung aus Induktivität und Verlustwiderstand in eine äquivalente Parallelschaltung umgerechnet werden: \[{R_{par}} = \frac{{R_{rei}^2 + X_{rei}^2}}{{{R_{rei}}}}\quad \quad {X_{par}} = \frac{{R_{rei}^2 + X_{rei}^2}}{{{X_{rei}}}}\] Die Formeln vereinfachen sich, wenn der Wert des Drahtwiderstands sehr klein gegenüber dem Blindwiderstand bei Resonanz ist. Das gilt für Induktivitäten deren Güte größer 10 ist. In diesem Beispiel hat der Gütefaktor den Wert 31: \[\begin{array}{l} {R_{rei}} \ll {X_{rei}}\quad \Rightarrow \quad R_{rei}^2 + X_{rei}^2 \approx X_{rei}^2\\ {R_{par}} \approx \frac{{X_{rei}^2}}{{{R_{rei}}}}\quad \quad {X_{par}} \approx {X_{rei}} \end{array}\]
Das Ergebnis ist eine mit Zeigerdiagrammen gut zu beschreibende und zu berechnende Parallelschaltung aus zwei Blindwiderständen und einem Wirkwiderstand. Im Zeigerdiagramm der Parallelschaltung ist die an allen Bauteilen gleiche Spannung die Bezugsgröße. Strom und Spannung am Wirkwiderstand weisen keine Phasenverschiebung auf. Im Kondensatorzweig beträgt die Phasenlage zwischen Strom und Spannung +90°. Im Spulenzweig beträgt die Phasenlage zwischen Strom und Spannung −90°. Die Zweigströme sind direkt proportional zu den Leitwerten, mit denen das Zeigerdiagramm erstellt wird.
Für niedrige Frequenzen bestimmt der jeweilige induktive Blindleitwert das Verhalten der Schaltung. Bei hohen Frequenzen ist der jeweilige kapazitive Blindleitwert bestimmend. Nur bei der Resonanzfrequenz fo sind beide Blindleitwerte gleich. Wegen ihrer gegensätzlichen Phasenlage heben sie sich in ihrer Wirkung nach außen hin auf. Im Resonanzfall hat der Parallelschwingkreis die Eigenschaft eines Wirkwiderstands und der Phasenwinkel zwischen Strom und Spannung beträgt φ = 0°.
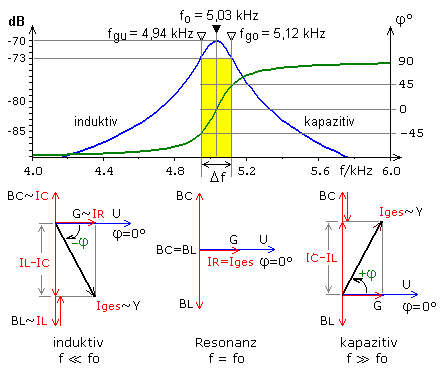
Für den Fall von ideal angenommenen Blindwiderständen wird durch Gleichsetzen beider Blindwiderstände oder Leitwerte die Resonanzfrequenz mithilfe der Schwingungsgleichung nach Thomson berechnet: \[\begin{array}{l} {X_L} = 2\,\pi \,f\,L\quad \quad {X_C} = \frac{1}{{2\,\pi \,f\,C}}\\ {X_L} = {X_C}\quad \Rightarrow \quad f = {f_o}\\ 2\,\pi \,{f_o}\,L = \frac{1}{{2\,\pi \,{f_o}\,C}}\quad \Rightarrow \quad {f_o} = \frac{1}{{2\,\pi \sqrt {L\,C} }} \end{array}\] In der oben dargestellten Durchlasskurve sind zwei weitere Frequenzen für die Phasenwinkel φ = ±45° eingezeichnet. Wie bei Hoch- und Tiefpassschaltungen lassen sich auch für den Schwingkreis Grenzfrequenzen definieren. Der Parallelschwingkreis verhält sich unterhalb der Resonanz mehr induktiv und oberhalb der Resonanz mehr kapazitiv. Bei den Grenzfrequenzen hat die Amplitude der Resonanzkurve mit −3 dB noch 70,7% ihres Maximalwertes. Die Differenz zwischen oberer und unterer Grenzfrequenz wird als Bandbreite bezeichnet.
Absolute Bandbreite
In einem kontinuierlichen Frequenzspektrum wird die Differenz zwischen einer hohen und niedrigen Frequenz allgemein als Bandbreite bezeichnet. Bei Schwingkreisen und elektronischen Filtern ist die absolute Bandbreite Δf der Bereich zwischen zwei Grenzfrequenzen oder dem Bereich von der maximalen Amplitude bis zur einzigen Grenzfrequenz. Im Amplituden-Frequenzgang des Parallelschwingkreises ist dieser Bereich gelb gekennzeichnet. Bei den Eckfrequenzen beträgt die maximale Amplitude der Resonanzfrequenz um −3 dB geringer. Die absolute Bandbreite berechnet sich zu: \[B = \Delta f = {f_{go}} - {f_{gu}}\]
Für gegebene C- und L-Werte eines Parallelschwingkreises wird die absolute Bandbreite durch den äquivalenten Parallelwiderstand und durch den Einkoppelwiderstand beeinflusst. Im Zeigerdiagramm ist zu erkennen, dass bei kleineren Leitwerten G, also größeren Widerstandswerten die Phasenwinkel φ von −90° ... 0° ... +90° schneller durchlaufen werden. Das Nutzsignal wird parallel zum Schwingkreis abgenommen und wird vom größeren Parallelwiderstand weniger belastet. Die Resonanzkurve verläuft steiler und ist schmaler. Schwingkreise mit idealem Verhalten gibt es nicht, da es keine absolut idealen Bauteile gibt. In fast allen Fällen bestimmt die geringere Güte der Spule die Bandbreite während der Kondensator einen deutlich höheren Gütefaktor hat.
Relative Bandbreite
Die relative Bandbreite ist das Verhältnis der absoluten Bandbreite dividiert durch die Resonanzfrequenz. Das Ergebnis ist ein benennungsloser Zahlenwert, der oft in Prozent angegeben wird: \[{B_{rel}} = b = \frac{B}{{{f_o}}}\]
Schwingkreisgüte
Je länger ein einmal angestoßener Schwingkreis mit gedämpfter Amplitude mit seiner Resonanzfrequenz schwingt oder je weniger Energie zur Aufrechterhaltung einer konstanten Schwingamplitude zugeführt werden muss, desto idealer ist sein Verhalten. Die Energieverluste sind proportional zum Wirkwiderstand oder Leitwert der realen Bauteile. Der Verlustfaktor einer realen Spule ist der Quotient aus dem ESR (Equivalent Series Resistance, Serienersatzwiderstand) und Blindwiderstand. Der mit dem Ohmmeter bestimmbare Drahtwiderstand entspricht dem ESR. Beim realen Kondensator kann kein ESR gemessen werden. Die Bestimmung des Verlustfaktors geht, wie es derzeit üblich ist, von der Reihenersatzschaltung des realen Kondensators aus. Die Güte ist der Kehrwert des Verlustfaktors. Je kleiner der ESR ist, desto idealer verhält sich das Bauteil. Die ESR-Werte können in ihre Parallelwerte umgerechnet werden. Im realen Parallelschwingkreis sind die beiden Blindwiderstände und Wirkwiderstände parallel geschaltet. Für den Energieverlust in Form von Wärme ist in erster Linie der Drahtwiderstand der Spule verantwortlich. Sie bestimmt mit ihrer geringeren Güte die Leerlaufgüte des Parallelschwingkreises.
Für den Verlustfaktor der Spule und den des Kondensators gilt: \[{d_L} = \tan \,\delta = \frac{{ES{R_L}}}{{{X_L}}}\quad \quad {d_c} = \tan \,\delta = ES{R_C} \cdot {X_C}\] Zur Vereinfachung wird angenommen: \(ES{R_L} = R\) und \(ES{R_C} \ll 0,1\,\Omega \approx 0\). Der Verlustfaktor der Spule bestimmt fast immer die Schwingkreisgüte. Sie berechnet sich in guter Näherung zu: \[\begin{array}{l} d = {d_L} + {d_C} \approx {d_L}\\ Q = \frac{1}{d} \approx \frac{1}{{{d_L}}} = \frac{{{X_L}}}{R} \end{array}\]
Die Leerlaufgüte eines realen Parallelschwingkreises verändert sich durch Hinzuschalten eines Parallelwiderstands, durch den Innenwiderstand der anregenden Signalquelle und durch jede weitere angeschlossene Last. Jede dieser Baugruppen beeinflusst die Betriebsgüte des Schwingkreises, die immer kleiner als die Leerlaufgüte ist. Die absolute Bandbreite wird ebenfalls beeinflusst und mit zunehmender Belastung größer. Die Leerlauf- und die Betriebsgüte sind aus dem Verhältnis der Resonanzfrequenz zur −3 dB Bandbreite bestimmbar: \[Q = \frac{{{f_o}}}{{\Delta f}} = \frac{{{f_o}}}{B}\]
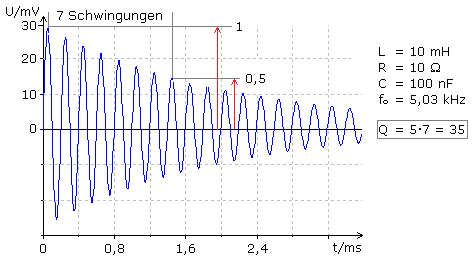
Wird ein Schwingkreis durch einen kurzen Energieimpuls auf seine Resonanzfrequenz angeregt, so kann die Güte aus der abklingenden Schwingungsfolge mit einem Oszillographen ermittelt werden. Die Methode ergibt bis rund 10 MHz brauchbare Ergebnisse. Es werden die Schwingungen gezählt bis die Anfangsamplitude auf die Hälfte abgenommen hat. Wird die Zahl mit dem Faktor 5 multipliziert, so ist das Ergebnis gleich der Güte. Das Bild zeigt für den Parallelschwingkreis mit den angegebenen Bauteilwerten die gedämpften Resonanzschwingungen. Nach der beschriebenen Methode beträgt die Güte Q = 35. Die Güte der Spule errechnet sich zu: \({Q_L} = {X_L}/10 = 2\,\pi \,{f_o}\,L/10 = 31,6\). Es ist der genauere Wert, da die Messfehler geringer als die Ablesefehler sind.
Resonanzwiderstand
Bei Resonanz sind die Werte der beiden Blindwiderstände gleich. Ihre Phasenbeziehungen zwischen Spannung und Strom sind gegenläufig und heben sich auf. Von außen gesehen verhält sich der Schwingkreis bei seiner Resonanz wie ein Wirkwiderstand. Ohne zusätzliche Dämpfung wird der Resonanzwiderstand Zo vom Drahtwiderstand der Spule bestimmt. Für den Parallelschwingkreis ist es der daraus umgerechnete äquivalente Parallelwiderstand. \[{Z_o} = {R_{par}} = \frac{{R_{rei}^2 + X_{rei}^2}}{{{R_{rei}}}}\quad \quad {X_{rei}} = {X_L} = \omega \,L\] Die beiden Blindwiderstände sind bei Resonanz gleich groß. Durch Einsetzen und Umformen folgt: \[\begin{array}{l} {Z_o} = {R_{rei}} + \frac{{\omega _o^2\,{L^2}}}{{{R_{rei}}}}\quad \quad {\omega _o}\,L = \frac{1}{{{\omega _o}\,C}}\\ {Z_o} = {R_{rei}} + \frac{L}{{C\,{R_{rei}}}} \end{array}\] Der Reihenwiderstand ist sehr klein im Vergleich zum Quotienten, somit gilt: \[{R_{rei}} \ll \frac{L}{{C\,{R_{rei}}}}\quad \Rightarrow \quad {Z_o} \approx \frac{L}{{C\,{R_{rei}}}}\]
Für die im Beispiel angegebenen Bauteilwerte hat der Schwingkreis die Resonanzfrequenz bei 5 kHz. Für den nach außen wirksamen äquivalenten parallelen Wirkwiderstand wurden 10 kΩ berechnet. Das gleiche Ergebnis wird mit der Formel für Zo erhalten und kann im Labor durch eine Spannungs- und Strommessung bei Resonanz ermittelt werden. Die Resonanzfrequenz scheint unabhängig von der Spulengüte oder einem entsprechenden Dämpfungswiderstand zu sein. Das gilt in der Praxis für Spulen hoher Güte und gering gedämpfte schmalbandige Parallelschwingkreise. Die genaue Berechnung zeigt eine kleine Abhängigkeit der Resonanzfrequenz vom Drahtwiderstand der Schwingkreisspule. Wird durch höhere Belastung die Bandbreite eines Parallelschwingkreises vergrößert, so wird Resonanzfrequenz etwas kleiner.
Die Resonanzfrequenz des realen Parallelschwingkreises
Für die genaue Herleitung der Formel für die Resonanzfrequenz sind beide Äquivalenzumrechnungen notwendig: \[{X_{par}} = \frac{{R_{rei}^2 + X_{rei}^2}}{{{X_{rei}}}}\quad \Rightarrow \quad {X_{par}} \cdot {X_{rei}} = R_{rei}^2 + X_{rei}^2\] Der parallele Blindwiderstand entspricht dem Kondensator, der Reihen-Blindwiderstand gehört zur Spule: \[{X_{par}} = \frac{1}{{\omega \,C}}\quad \quad {X_{rei}} = \omega \,L\] Durch Einsetzen und Umformen für den Resonanzfall folgt: \[\frac{{\omega \,L}}{{\omega \,C}} = R_{rei}^2 + {({\omega _o}\,L)^2}\quad \Rightarrow \quad \omega _o^2 = \frac{L}{{{L^2}\,C}} - \frac{{R_{rei}^2}}{{{L^2}}}\] Aufgelöst nach der Resonanzfrequenz: \[{f_o} = \frac{1}{{2\,\pi }}\sqrt {\frac{1}{{L\,C}} - {{\left( {\frac{{{R_{rei}}}}{L}} \right)}^2}} \] Wird ein sehr kleiner Wert des Drahtwiderstands vernachlässigt, dann ist das Ergebnis die bekannte Schwingkreisformel nach Thomson: \[{R_{rei}} \to 0\quad \Rightarrow \quad {f_o} = \frac{1}{{2\,\pi \sqrt {L\,C} }}\]
Bei einem Parallelschwingkreis mit C = 100 nF und L = 10 mH wurde die Spulengüte QL durch in Reihe geschaltete Widerstände verschlechtert. Die Tabelle zeigt eine geringe Verschiebung der Resonanzfrequenz zu niedrigeren Werten. Da ein Schwingkreis mit einer Betriebsgüte kleiner 10 praktisch nicht sinnvoll ist, bleibt die Frequenzdrift vernachlässigbar gering.
| Rv/Ω | 5 | 10 | 50 | 100 | 150 |
|---|---|---|---|---|---|
| QL | 63 | 32 | 6,3 | 3,2 | 2 |
| f0/kHz | 5,033 | 5,030 | 4,970 | 4,775 | 4,431 |
Parallelschwingkreise werden vielfach im Tuner als Abstimmkreis zur Senderwahl, als Arbeitswiderstand im Resonanzverstärker, bei Oszillatoren sowie als Sperrkreis zum Ausfiltern eng begrenzter Frequenzbereiche eingesetzt. Es folgt eine Zusammenstellung für wichtige Eigenschaften eines Parallelschwingkreises:
Bei Resonanz verhält sich ein Parallelschwingkreis nach außen wie ein Wirkwiderstand.
Die Impedanz des Parallelkreises hat bei Resonanz ihren größten Wert.
Bei Resonanz ist der in den Kreis fließende Gesamtstrom am kleinsten.
Durch Resonanzüberhöhung sind die Blindströme im Kreis maximal und größer als der außen messbare Gesamtstrom.
Die Leerlaufgüte wird ohne zusätzliche Belastungen vom Drahtwiderstand der Spule bestimmt.
Die Betriebsgüte ist immer kleiner als die Leerlaufgüte.
Die Bandbreite ist umgekehrt proportional zur Kreisgüte.
Die Resonanzfrequenz wird mit zunehmender Kreisdämpfung etwas niedriger.
Herleitungen der Grenzfrequenzgleichungen
Die charakteristischen Frequenzen eines Schwingkreises sind die Resonanzfrequenz und die beiden Grenzfrequenzen, mit denen die Bandbreite bestimmt werden kann. Experimentell können sie mit einem Frequenzgenerator und Oszillographen recht einfach ermittelt werden. Sie sollen nachfolgend mathematisch hergeleitet werden. Per Definition hat der Phasenwinkel bei den Grenzfrequenzen den Wert φ = ±45°, wobei das Vorzeichen den mehr induktiven oder kapazitiven Charakter der Schaltung anzeigt. Der Phasenwinkel von |45°| ist genau dann gegeben, wenn beim Schwingkreis die Differenz der Blindleitwerte für Spule und Kondensator, gleich dem Wirkleitwert ist: \[\varphi = \left| {{{45}^o}} \right|\quad \quad G = {B_c} - {B_L}\quad \quad G = {B_L} - {B_c}\] Die Herleitung der oberen Grenzfrequenz für den Resonanzfall erfolgt mit äquivalentem Drahtwiderstand der Spule: \[\frac{1}{R} = {\omega _{go}}\,C - \frac{1}{{{\omega _{go}}\,L}}\quad \Rightarrow \quad \omega _{go}^2\,L\,C - \frac{{{\omega _{go}}\,L}}{R} = 1\] Nach dem Multiplizieren mit 1/LC folgt mit der Schwingungsformel nach Thomson: \[\omega _{go}^2 - {\omega _{go}}\frac{1}{{R\,C}} = \frac{1}{{L\,C}}\quad \Rightarrow \quad \omega _{go}^2 - {\omega _{go}}\frac{1}{{R\,C}} = \omega _o^2\] Mit der quadratischen Ergänzung und dem Anwenden des binomischen Lehrsatzes folgt: \[{\omega _{go}} = \sqrt {\omega _o^2 + {{\left( {\frac{1}{{2\,R\,C}}} \right)}^2}} + \frac{1}{{2\,R\,C}}\quad \quad {\omega _{go}} = 2\,\pi \,{f_{go}}\] Für die obere Grenzfrequenz bei Resonanz gilt: \[{f_{go}} = \frac{1}{{2\,\pi }}\left( {\sqrt {\omega _o^2 + {{\left( {\frac{1}{{2\,R\,C}}} \right)}^2}} + \frac{1}{{2\,R\,C}}} \right)\quad (1)\] Entsprechend ergibt die Herleitung für die untere Grenzfrequenz bei Resonanz: \[{f_{gu}} = \frac{1}{{2\,\pi }}\left( {\sqrt {\omega _o^2 + {{\left( {\frac{1}{{2\,R\,C}}} \right)}^2}} - \frac{1}{{2\,R\,C}}} \right)\quad (2)\]
Mit der hergeleiteten Gl.(1) und Gl.(2) kann die absolute Bandbreite ermittelt werden. Für den Wirkwiderstand R wird der äquivalente Parallelwiderstand des Spulendrahtes eingesetzt: \[B = \Delta f = {f_{go}} - {f_{gu}}\quad \Rightarrow \quad B = \frac{1}{{2\,\pi \,R\,C}}\] Die obere Grenzfrequenz mit Gl.(1) berechnet hat den Wert fgo = 5,109 kHz und die untere Grenzfrequenz mit Gl.(2) ergibt fgu = 4,950 kHz. Die absolute Leerlaufbandbreite bei Resonanz beträgt B = 159 und ist gut vergleichbar mit dem weiter oben abgelesenen Wert Δf = 180 aus der Simulationsschaltung.
Beim Parallelschwingkreis liegen die Grenzfrequenzen nahezu symmetrisch zur Resonanzfrequenz. Diese Aussage gilt auch für den Reihenschwingkreis. Die Resonanzfrequenz kann als Mittenfrequenz aus dem geometrischen Mittel der beiden Grenzfrequenzen errechnet werden: \[{f_o} = \sqrt {{f_{gu}} \cdot {f_{go}}} \quad \quad {f_o} = \sqrt {4,950 \cdot 5109} \,kHz = 5,03\,kHz\]