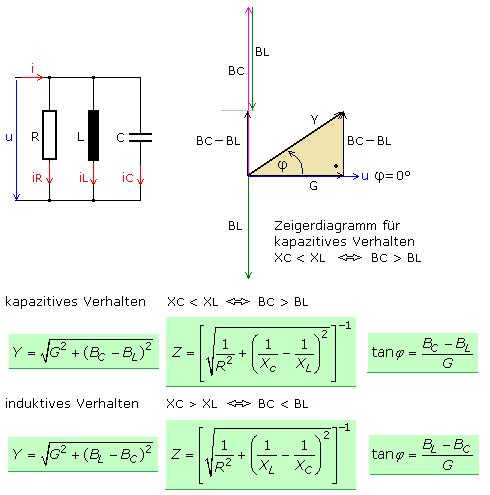
RLC-Zeigerdiagramme im Wechselstromkreis

Alle folgenden Erklärungen und Beschreibungen beziehen sich auf eine sinusförmige Betriebsspannung. Wirk- und Blindwiderstände verhalten sich im Wechselstromkreis unterschiedlich. Bei der Berechnung des Gesamtwiderstands einer gemischten Reihen- oder Parallelschaltung ist das zu berücksichtigen. Der Gesamtwiderstand einer Schaltung im Wechselstromkreis wird als Scheinwiderstand wird ganz allgemein als Impedanz Z bezeichnet. Für die Gesamtschaltung gilt das Ohmsche Gesetz. Die Impedanz kann aus den Messwerten der anliegenden Spannung und dem daraus resultierenden Gesamtstrom errechnet werden. Der Spannungswert ist proportional zur Impedanz. Ihr Kehrwert ist der Scheinleitwert und verhält sich proportional zum Gesamtstrom.

Beschrieben werden folgende Kombinationen aus Wirk- und Blindwiderständen an einer Sinusspannung:
RC-Reihenschaltung, RL-Reihenschaltung, RCL-Reihenschaltung, RC-Parallelschaltung, RL-Parallelschaltung, RCL-Parallelschaltung.

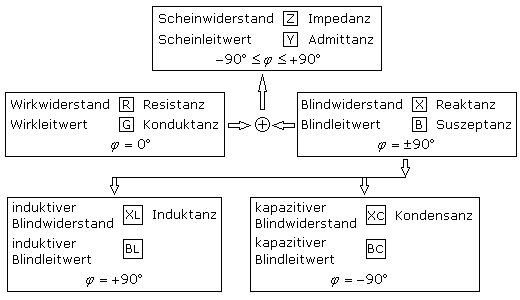
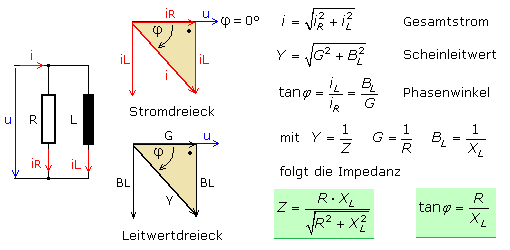
Das Bild zeigt den Stammbaum der Wechselstromwiderstände und Leitwerte. Neben den deutschen sind auch die lateinischen Bezeichnungen angegeben. Hierbei ist der Strom als Bezugsgröße mit der Phasenlage von 0° gesetzt.

In allen Zeigerdiagrammen ist die x-Achse als reelle Achse mit den Wirkanteilen verbunden. Am Ohmschen oder Wirkwiderstand sind Strom und Spannung zueinander phasengleich, φ = 0°. Auf der senkrechten y-Achse werden die Blindkomponenten abgetragen. Bei allen Blindgrößen ist die Phasenverschiebung zwischen Strom und Spannung genau φ = ±90°. Da es keine wirklich idealen Baugruppen gibt, kann jede Wechselstromgröße in ihre Wirk- und Blindkomponenten zerlegt werden. Sind die Einzelgrößen von R, L und C und die Frequenz bekannt, dann lassen sich mithilfe der Zeigerdiagramme viele wichtige Eigenschaften der Gesamtschaltung ermitteln.

Im rechtwinkligen Koordinatensystem ist ein Zeiger charakterisiert durch seine Länge und den Winkel, den er mit der horizontalen x-Achse bildet. Jeder Zeiger kann in der Darstellungsebene unter Beibehaltung seiner Eigenschaften parallel zur x- und y-Achse verschoben werden.

Reihenschaltungen an Sinusspannung

RC-Reihenschaltung

In einer Reihenschaltung ist der Strom an jeder Messstelle gleich und ist die Bezugsgröße der Reihenschaltung. Per Definition wird der Stromzeiger als Bezugsgröße in x-Achsenrichtung mit dem Phasenwinkel φ = 0° gezeichnet. Ein Zeiger beginnt zweckmäßig im Koordinatennullpunkt. In der Elektronik erfolgt die Umlaufrichtung der Zeiger immer gegen den Uhrzeigersinn. Der Drehwinkel hat bei Linksdrehung ein positives Vorzeichen und in der Gegenrichtung mit dem Uhrzeigersinn ein negatives Vorzeichen. Wird das Zeigerdiagramm für eine Reihenschaltung gezeichnet, so sind die folgenden allgemeingültigen Tatsachen zu berücksichtigen:

Der Strom ist die Bezugsgröße. Am Ohmschen Wirkwiderstand sind Strom und Spannung mit φ = 0° in Phase. Am kapazitiven Blindwiderstand eines idealen Kondensators läuft die Spannung dem Strom mit dem Phasenwinkel φ = −90° nach.

Mit diesen Aussagen kann für jede RC-Reihenschaltung das Zeigerdiagramm gezeichnet werden. Aus dem Diagramm lassen sich wichtige Eigenschaften der Schaltung herleiten. Zur Ermittlung der Gesamtspannung u müssen die Teilspannungen geometrisch addiert werden. Dazu wird der Zeiger für uC nach rechts, parallel bis an die Spitze des Zeigers uR verschoben. Beide Teilspannungen bilden die Katheten eines rechtwinkligen Dreiecks. Seine Hypotenuse entspricht der Gesamtspannung u. Das so entstandene gelbe Dreieck wird Spannungsdreieck oder Zeigerdiagramm der Spannungen genannt.

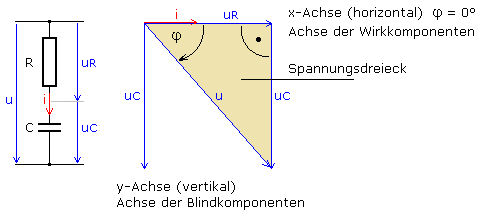
Für das Spannungsdreieck gelten die Winkelsätze des rechtwinkligen Dreiecks und der Lehrsatz des Pythagoras. Er besagt, dass die Flächensumme der Kathetenquadrate gleich der Fläche des Hypotenusenquadrats ist. Die Gleichung zur Berechnung der Gesamtspannung aus den Teilspannungen leitet sich wie folgt her:

Das Ohmsche Gesetz gilt generell auch bei Wechselgrößen. Sind die Teilspannungen der einzelnen Widerstände und der Strom bekannt, lässt sich jeder einzelne Widerstandswert errechnen. Da die Spannungen proportional zu den jeweiligen Widerstandswerten sind, können die Teilspannungen im Spannungsdreieck durch die Widerstandswerte ersetzt werden. Anstelle von uR steht dann R und uC wird durch XC ersetzt. Die Gesamtspannung u ist am Gesamtwiderstand, dem Scheinwiderstand oder der Impedanz Z messbar. Das Zeigerdiagramm der Widerstände ist proportional zum Zeigerdiagramm der Spannungen.

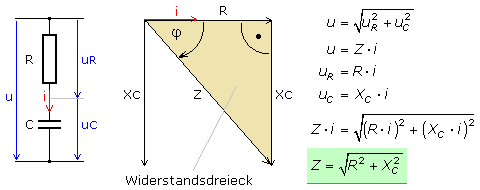
Der Phasenverschiebungswinkel φ

Der Phasenwinkel gibt die Phasenlage zwischen der an der Schaltung anliegenden Spannung und dem Gesamtstrom an. In der Reihenschaltung wird dem Strom als Bezugsgröße der Winkel φ = 0° zugeordnet. Die Phasenlage im Spannungsdreieck wird vom Winkel zwischen der Gesamtspannung an der Impedanz Z und Wirkspannung an R bestimmt. Im Widerstandsdreieck liegt der Phasenwinkel zwischen dem Impedanz- und Wirkwiderstandszeiger. Das Verhältnis aus Gegenkathete zur Ankathete stellt die Tangensfunktion des Phasenwinkels dar. Der Winkel errechnet sich aus der Umkehrfunktion, dem Arcustangens.

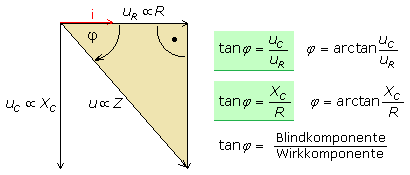
Auf vielen Taschenrechnern lassen sich die Winkelumkehrfunktionen mit der Taste: Winkelfunktion⁻¹, hier tan⁻¹ aufrufen. Diese Exponentialdarstellung ist nicht identisch mit dem mathematischen Kehrwert 1/tan(φ). Zusammenfassend gilt für eine RC-Reihenschaltung an Wechselspannung:

Die Gesamtspannung ist die Wurzel aus der Summe der Quadrate der Teilspannungen.
Die Impedanz ist die Wurzel aus der Summe der Quadrate der Wechselstromwiderstände.
Der Tangens des Phasenwinkels errechnet sich aus dem Quotienten der Blind- zur Wirkkomponente.
Die Gesamtspannung eilt dem Gesamtstrom um den Phasenwinkel φ nach.

RL-Reihenschaltung

In der Reihenschaltung aus einem ohmschen Wirkwiderstand und dem Blindwiderstand einer Spule, einer Induktivität, ist der Strom die Bezugsgröße mit dem Phasenwinkel φ = 0°. Am Wirkwiderstand sind Spannung und Strom stets in gleicher Phasenlage.

Am idealen induktiven Blindwiderstand einer Spule eilt die Spannung dem Strom um φ = +90° voraus.

Unter Berücksichtigung dieser Tatsachen können die Zeigerdiagramme für Spannungen und Widerstände erstellt werden. Die Herleitungen für das Spannungsdreieck, das Widerstandsdreieck und den Phasenwinkel sind vergleichbar mit der RC-Reihenschaltung.

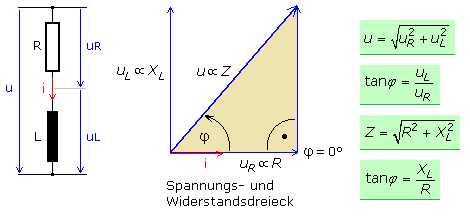
Die Gesamtspannung und die Impedanz werden durch die geometrische Addition der entsprechenden Teilgrößen errechnet.
Die Gesamtspannung eilt dem Strom um den Phasenwinkel φ voraus.

RCL-Reihenschaltung

Das Zeigerdiagramm ist eine Kombination der beiden zuvor beschriebenen Reihenschaltungen. Der Strom ist die Bezugsgröße und der Stromzeiger weist in die x-Richtung mit φ = 0°. Spannung und Strom am Wirkwiderstand sind in Phase. Die Spannung am kapazitiven Blindwiderstand hat einen Phasenwinkel von φ = −90°. Die Spannung am induktiven Blindwiderstand hat den Phasenwinkel von φ = +90°.

Die einzelnen Zeiger sind geometrisch zu addieren. Dazu müssen die in y-Richtung liegenden Zeiger der Blindkomponenten so vertikal verschoben werden, dass der kürzere Zeiger mit seinem Anfang an das Ende des längeren Zeigers anliegt. Der daraus resultierende Summenzeiger wird horizontal parallel an die Spitze des Zeigers der Wirkkomponente verschoben, wodurch das rechtwinklige Dreieck entsteht. Damit lassen sich alle Gleichungen herleiten.

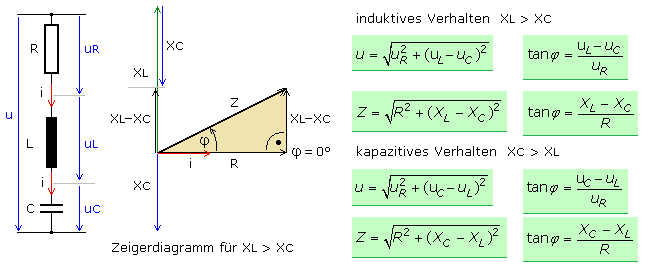
In Abhängigkeit von den Zeigerlängen nimmt der Phasenwinkel zwischen Strom und Spannung positive oder negative Werte an. Die RCL-Reihenschaltung wirkt nach außen hin mit +φ mehr induktiv und mit −φ mehr kapazitiv. Die Zeiger beider Blindkomponenten weisen mit 180° in entgegengesetzte Richtungen. Für eine charakteristische Frequenz sind sie gleich lang und ihre Beträge heben sich rechnerisch auf. Mit dem verbleibenden ohmschen Wirkanteil verhält sich die Schaltung dann insgesamt wie ein ohmscher Widerstand, bei dem Strom und Spannung in Phase sind. Zu diesem Sonderfall einer RLC-Reihenschaltung gibt es im Kapitel Reihenschwingkreis weiterführende Informationen.

Parallelschaltungen an Sinusspannung

RC-Parallelschaltung

Widerstände liegen in einer Parallelschaltung alle an derselben Spannung, die im Zeigerdiagramm zur Bezugsgröße wird. Der Spannungszeiger weist in x-Achsenrichtung mit dem Winkel φ = 0°. Am Wirkwiderstand weist der Stromzeiger in die gleiche Richtung, da der Phasenwinkel 0° beträgt. Am kapazitiven Blindwiderstand eilt der Strom um +90° voraus und der Stromzeiger zeigt in die positive y-Achsenrichtung.

Es kann ein rechtwinkliges Stromdreieck gezeichnet werden. Der Gesamtstrom errechnet aus der geometrischen Addition der Teilströme. Der Phasenwinkel zwischen Spannung und Strom ergibt sich aus tanφ, dem Quotienten von Blindkomponente zur Wirkkomponente. Die Teilströme sind direkt proportional zu den Leitwerten. Das Stromdreieck kann folglich in ein verhältnisgleiches Leitwertdreieck umgezeichnet werden. Die Leitwerte lassen sich durch die Kehrwerte der entsprechenden Widerstandswerte ersetzen.

RL-Parallelschaltung

Die an der Parallelschaltung anliegende Wechselspannung ist die Bezugsgröße. Am Wirkwiderstand sind Spannung und Strom mit φ = 0° in Phase. Am induktiven Blindwiderstand der Spule eilt der Strom um φ = −90° der Spannung nach. Die mathematischen Beziehungen lassen sich aus dem Zeigerdiagramm leicht herleiten.

RCL-Parallelschaltung

Die Bezugsgröße mit φ = 0° ist die Wechselspannung. Spannung und Strom am ohmschen Wirkwiderstand sind phasengleich. Am kapazitiven Blindwiderstand eilt der Strom um φ = +90° vor und am induktiven Blindwiderstand um φ = −90° nach. Durch entsprechende Parallelverschiebung der Zeiger kann das Stromdreieck und daraus abgeleitet das Leitwertdreieck gezeichnet werden.

Der Phasenwinkel kann positive oder negative Werte annehmen, je nachdem ob die Induktivität oder die Kapazität mit ihren Werten den Schaltungscharakter bestimmt. Sind beide Blindkomponenten gleich groß, so wirkt die RCL-Parallelschaltung nach außen hin wie ein ohmscher Widerstand mit φ = 0°. Dieser Fall wird im Kapitel Parallelschwingkreis ausführlich beschrieben.