Impedanzberechnungen im Wechselstromkreis

Umfangreichere Widerstandsnetzwerke mit nur realen Wirkwiderständen (R) können recht einfach mit dem Ohm'schen Gesetz der Reihen- und Parallelschaltung berechnet werden. Das Umzeichnen und Zusammenfassen von Widerstandsnetze gilt gleichermaßen für die Gleich- und Wechselstromtechnik.

In Schaltungen der Wechselstromtechnik mit zusätzlich kapazitiven und induktiven Blindwiderständen weisen Spannungen und Ströme zueinander Phasenwinkel auf. Sie sind bei der Berechnung des Gesamtwiderstands, als Impedanz (Z) bezeichnet, zu berücksichtigen. Die genaue Kenntnis und richtige Anwendung der Zeigerdiagramme liefert den Schlüssel zum Berechnungsansatz. Kombinierte LC-Widerstandsnetzwerke mit Reihen- und Parallelschaltungen der Bauteile können in ihre Äquivalentschaltungen umgerechnet werden. Am Ende erhält man eine reine Reihen- oder Parallelschaltung aus Blind- und Wirkwiderständen mit unveränderten Eigenschaften. Die Impedanz der Schaltung kann grafisch und rechnerisch mithilfe des entsprechenden Zeigerdiagramms bestimmt werden.

Der Einsatz der komplexen Rechnung ist dem grafischen Verfahren fast immer überlegen. Wissenschaftliche Taschenrechner verfügen über einprogrammierte Algorithmen, die schnell das gewünschte Ergebnis anzeigen. Jeder Nutzer sollte sich zuvor mit der Bedienung des Rechners vertraut machen, da es hierfür keine genormten Ein- und Ausgabeverfahren gibt. Für die Tasten R→P, P→R, teilweise POL und x→y sind die notwendigen Umrechnungsformeln fest programmiert und lassen sich direkt nutzen.

Äquivalente Schaltungen

Eine Reihenschaltung mit Wirk- und Blindwiderständen kann in ihre gleichwertige Parallelschaltung umgerechnet werden. Beide Schaltungen sind genau dann äquivalent, wenn für eine bestimmte Frequenz die Impedanz Z, also der Gesamtwiderstand und der Phasenwinkel gleich sind. Im folgenden Beispiel wird eine Reihenschaltung mithilfe der komplexen Rechnung in ihre gleichwertige Parallelschaltung umgerechnet. Die Reihenschaltung besteht aus dem Wirkwiderstand Rreih = 100 Ω und der Spule mit Lreih = 40 mH. Für die Frequenz f = 800 Hz sind die Bauteilwerte der dazu äquivalenten Parallelschaltung mit Rpar und Lpar gesucht.

Der Wirkwiderstand ist von der Frequenz unabhängig. Der Blindwiderstand der Spule errechnet sich zu \({X_{L\,reih}} = 2\,\pi \,f\,L = 200\,\Omega \). Die Bezugsgröße jeder Reihenschaltung ist der Strom in Richtung der reellen Achse (Re). Der Operator des Wirkwiderstands liegt auf der reellen Achse mit der Zeigerlänge für 100 Ω. Die Spannung an der Spule eilt dem Strom um 90° voraus. Der Operator des induktiven Blindwiderstands mit der Zeigerlänge 200 Ω liegt auf der positiven imaginären Achse (Im). Die Impedanz (Scheinwiderstand) der Reihenschaltung errechnet sich aus der geometrischen Summe der beiden Widerstandsoperatoren: \[Z = \sqrt {R_{reih}^2 + X_{Lreih}^2} = \sqrt {{{100}^2} + {{200}^2}} \;\Omega = 223,6\;\Omega \] Die Eingangsspannung liegt an der Impedanz und der Strom fließt gleichermaßen durch beide Bauteile. Der Phasenwinkel zwischen der Eingangsspannung und dem Strom kann aus dem Arkuskosinus des Verhältnisses der Ankathete zur Hypotenuse ebenso wie aus dem Arkustangens des Quotienten der Gegenkathete zur Ankathete berechnet werden: \[\varphi = {\mathop{\rm arc}\nolimits} \,tan\left( {\frac{{{X_{L\,reih}}}}{{{R_{reih}}}}} \right) = {\mathop{\rm arc}\nolimits} \,tan\frac{{200}}{{100}} = {63,4^0}\]

Die äquivalente Parallelschaltung muss in der Impedanz und dem Phasenwinkel zwischen Spannung und Strom gleich sein. Bei einer Parallelschaltung ist die Spannung die Bezugsgröße und weist in die Richtung der reellen Achse. Es wird das Zeigerdiagramm der Leitwertoperatoren verwendet. Der Scheinleitwert (Admittanz) ist gleich dem Kehrwert der Impedanz: \(\underline Y = 1/\underline Z \). Diese Impedanz soll gleich der Reihenimpedanz sein: \[\begin{array}{l} {\underline Y _{par}} = \frac{1}{{{{\underline Z }_{reih}}}}\quad \quad \\ {\underline Y _{par}} = \frac{1}{{{R_{reih}} + j\,{X_{L\,reih}}}} = \frac{1}{{100\,\Omega + j\,200\,\Omega }} \end{array}\] Der Nenner wird durch konjugiert komplexe Erweiterung real: \[\begin{array}{l} {\underline Y _{par}} = \frac{{100\,\Omega - j\,200\,\Omega }}{{(100\,\Omega + j\,200\,\Omega )(100\,\Omega - j\,200\,\Omega )}}\quad {j^2} = - 1\\ {\underline Y _{par}} = \frac{{100\, - j\,200\,}}{{50000}}S \end{array}\] Getrennt in Real- und Imaginärkomponenten geschrieben sind das die Leitwertkomponenten der Parallelschaltung: \[\begin{array}{l} {\underline Y _{par}} = 0,002\,S - j \cdot 0,004\,S\\ \left| {{{\underline Y }_{par}}} \right| = \sqrt {{{{\mathop{\rm Re}\nolimits} }^2} + {{{\mathop{\rm Im}\nolimits} }^2}} = \sqrt {4 \cdot {{10}^{ - 6}} + 16 \cdot {{10}^{ - 6}}} \,S = 4,472 \cdot {10^{ - 3}}\,S \end{array}\] Ihre Kehrwerte sind die gesuchten Widerstandswerte der äquivalenten Parallelschaltung: \[\begin{array}{l} \left| {{{\underline Z }_{par}}} \right| = \frac{1}{{4,472 \cdot {{10}^{ - 3}}\,S}} = 223,6\;\Omega \\ {R_{par}} = \frac{1}{{0,002\,S}} = 500\;\Omega \\ {X_{L\,par}} = \frac{1}{{0.004\,S}} = 250\;\Omega \quad \Rightarrow \quad {L_{par}} = \frac{{250\,\Omega }}{{2\,\pi \,800\,Hz}} = 50\;mH \end{array}\] Die äquivalente Parallelschaltung hat dieselbe Impedanz wie die gegebene Reihenschaltung. Der Phasenwinkel kann mithilfe des Arkustangens aus dem Quotienten des Blindleitwerts zum Wirkleitwert berechnet werden. Das Vorzeichen kehrt sich wegen der geänderten Bezugsgröße auf die Spannung um. \[\varphi = {\mathop{\rm arc}\nolimits} \,tan\left| {\left( {\frac{{ - {B_{L\,par}}}}{{{G_{L\,par}}}}} \right)} \right| = {\mathop{\rm arc}\nolimits} \,tan\left| {\left( {\frac{{ - 0,004}}{{0,002}}} \right)} \right| = {63,4^0}\]

Gemischte Widerstandsnetzwerke

Für das folgende gemischte Widerstandsnetzwerk werden mithilfe der komplexen Rechnung die Impedanz und der Phasenwinkel zwischen Spannung und Strom bei sinusförmiger Eingangsspannung errechnet. Die RC-Parallelschaltung und die RL-Reihenschaltung, können voneinander unabhängig berechnet werden. Das Ergebnis sind zwei Teilimpedanzen mit zwei von 90° verschiedenen Phasenwinkeln. Ein einfaches Zusammenfassen unter Anwendung des Satzes des Pythagoras ist nicht möglich.

Alle Widerstandswerte sind gegeben oder lassen sich aus den Bauteilwerten und der Frequenz berechnen. Je nach Art der Teilschaltung werden entweder die komplexen Leitwertoperatoren oder Widerstandsoperatoren zur Berechnung benutzt. Im Polardiagramm der Gaußschen Zahlenebene ist die Lage der Operatoren eines Wirkwiderstands und seines Leitwerts wegen des Phasenwinkels φ = 0° unabhängig von der Bezugsgröße. Sie liegen immer auf der reellen Achse. Ein kapazitiver Blindwiderstand weist auf der negativen imaginären Achse nach unten. Der kapazitive Blindleitwert weist auf der positiven imaginären Achse nach oben. Die Zeigerlänge entspricht dem errechneten Widerstandswert oder dem reziproken Leitwert. Beim induktiven Blindwiderstand und Blindleitwert ist es umgekehrt. Die Operatoren eines Blindwiderstands und seines Leitwerts sind an der reellen Achse gespiegelt.

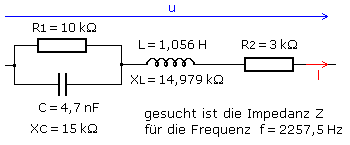
Die Normalform des Scheinleitwerts Ypar (Admittanz) errechnet sich durch Addition der Leitwertoperatoren zu: \[\begin{array}{l} {\underline Y _{par}} = {\underline Y _R} + {\underline Y _C} = {G_1} + j\,\omega \,C\\ {\underline Y _{par}} = 1\,mS + j \cdot 2,9531\,mS\\ \left| {{{\underline Y }_{par}}} \right| = \sqrt {{{{\mathop{\rm Re}\nolimits} }^2} + {{{\mathop{\rm Im}\nolimits} }^2}} = \sqrt {9,721 \cdot {{10}^{ - 6}}} \,mS = 3,118\,mS \end{array}\] Die Normalform des Scheinwiderstands (Impedanz) errechnet sich durch Addition der Widerstandsoperatoren zu: \[\begin{array}{l} {\underline Z _{reih}} = {\underline Z _R} + {\underline Z _L} = {R_2} + j\,\omega \,L\\ {\underline Z _{reih}} = 1\,k\Omega + j \cdot 0,6283\,k\Omega \\ \left| {{{\underline Z }_{reih}}} \right| = \sqrt {{{{\mathop{\rm Re}\nolimits} }^2} + {{{\mathop{\rm Im}\nolimits} }^2}} = \sqrt {1,3948 \cdot {{10}^6}} k\Omega = 1,181\,k\Omega \end{array}\] Die Simulation der Schaltung ergab die eingetragenen Messwerte für die Teilspannungen und den Gesamtstrom. Die Berechnung der Teilimpedanzen mit diesen Werten ergibt für die Parallelschaltung den Wert Zpar = 320,7 Ω und für die Reihenschaltung den Wert Zreih = 1180,5 Ω Der mathematische Ansatz ist damit bestätigt.

Die Gesamtimpedanz der Schaltung kann durch die Addition der komplexen Teilimpedanzen erhalten werden: \[\begin{array}{l} {\underline Z _{ges}} = {\underline Z _{reih}} + {\underline Z _{par}} = {\underline Z _{reih}} + \frac{1}{{{{\underline Y }_{par}}}}\\ {\underline Z _{ges}} = 1 \cdot {10^3} + j \cdot 0,6283 \cdot {10^3} + \frac{1}{{1 \cdot {{10}^{ - 3}} + j \cdot 2,9531 \cdot {{10}^{ - 3}}}} \end{array}\] Den Bruch konjugiert komplex erweitern und die rechte Seite in die Re- und Im-Komponente getrennt schreiben: \[\begin{array}{l} {\underline Z _{ges}} = 1 \cdot {10^3} + j \cdot 0,6283 \cdot {10^3} + \frac{{1 \cdot {{10}^{ - 3}} - j \cdot 2,9531 \cdot {{10}^{ - 3}}}}{{9,7208 \cdot {{10}^{ - 6}}}}\\ {\underline Z _{ges}} = 1102,9 + j \cdot 324,51\\ \left| {{{\underline Z }_{ges}}} \right| = \sqrt {{{{\mathop{\rm Re}\nolimits} }^2} + {{{\mathop{\rm Im}\nolimits} }^2}} = \sqrt {1,3217 \cdot {{10}^6}} = 1149,6\;\Omega \end{array}\] Der berechnete Gesamtwiderstand dieser gemischten Schaltung entspricht dem Messwert Rges = 1149,4 Ω der Simulationsschaltung. In der Simulation abgelesene Phasenwinkel mit einer Ablesegenauigkeit von ca. 0,5° zwischen der Eingangsspannung und dem Strom beträgt φ = 16°. Mit der komplexen Wechselstromrechnung wird mit dem Arkustangens des Quotienten der Imaginärkomponente zur Realkomponente der Phasenwinkel berechnet: \[\varphi = \arctan \left( {\frac{{{\mathop{\rm Im}\nolimits} }}{{{\mathop{\rm Re}\nolimits} }}} \right) = \arctan \left( {\frac{{324,51}}{{1102,9}}} \right) = {16,4^0}\]